Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Основы логики 9 класс
Содержание
- 1. Основы логики 9 класс
- 2. СодержаниеАлгебра логикиЛогические высказыванияОсновные логические операцииДополнительные логические операцииЛогические основы работы компьютераЗаконы и тождества алгебры логики
- 3. Алгебра логики Алгебра логики — это математический аппарат,
- 4. Логические высказывания Логическое высказывание — это любое повествовательное
- 5. Определить истинность сложных высказываний:Суффикс – это часть
- 6. Логические высказывания принято обозначать буквами английского алфавита:
- 7. Основные логические операции Существует три основные логические операции:
- 8. Отрицание (инверсия, не) Инверсия истинна тогда, когда само высказывание ложно, и ложно, когда высказывание истинно. Обозначение: Таблица истинности:
- 9. Дизъюнкция (логическое сложение, или) Дизъюнкция (логическое сложение) двух
- 10. Конъюнкция (логическое умножение, и) Конъюнкция (логическое умножение) двух
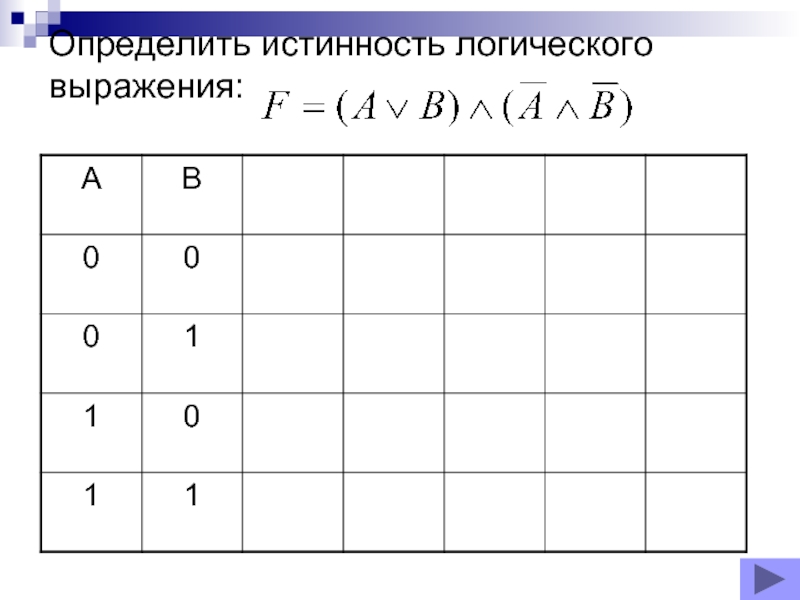
- 11. Определить истинность логического выражения:
- 12. Слайд 12
- 13. Слайд 13
- 14. Дополнительные логические операции Логическое следование (импликация, если…,
- 15. Равнозначность (эквивалентность, тогда и только тогда, когда) Эквивалентность
- 16. Порядок выполнения логических операций в сложном логическом
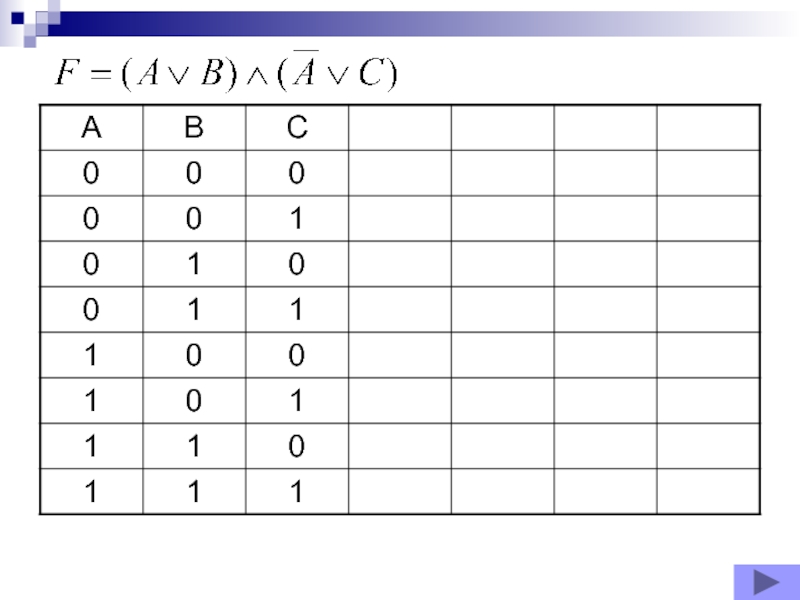
- 17. Определить истинность логического выражения:
- 18. Слайд 18
- 19. Логические основы работы компьютера Компьютер работает на электричестве,
- 20. Логический элемент «И» На выходы А и В
- 21. Логический элемент «ИЛИ» На входы А и В
- 22. Логический элемент «НЕ» На вход А логического элемента
- 23. По схеме составить логическое выражение и определить его истинность
- 24. Законы и тождества алгебры логики1. Коммутативный закон: A Λ
- 25. 4. Закон противоречия: 5. Закон исключенного третьего: 6. Закон двойного отрицания: 7. Законы де Моргана:
- 26. 8. Законы повторения: A Λ A = A;
- 27. Список источниковhttp://book.kbsu.ru/theory/chapter5/1_5_1.htmlhttp://www.webmath.ru/poleznoe/tables_istinnosti.phphttp://www.inf1.info/book/export/html/210
- 28. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Основы логики
9 класс
Автор: Андреева Анна Викторовна, учитель информатики МБОУ СОШ
№1 г. Лакинска Собинского района
Слайд 2Содержание
Алгебра логики
Логические высказывания
Основные логические операции
Дополнительные логические операции
Логические основы работы компьютера
Законы
и тождества алгебры логики
Слайд 3Алгебра логики
Алгебра логики — это математический аппарат, с помощью которого
записывают, вычисляют, упрощают и преобразовывают логические высказывания.
Создателем алгебры
логики является живший в XIX веке английский математика Джордж Буль, в честь которого эта алгебра названа булевой алгеброй высказываний.
Слайд 4Логические высказывания
Логическое высказывание — это любое повествовательное предложение, в отношении
которого можно однозначно сказать, истинно оно или ложно.
Киев –
столица Беларуси.Невозможно создать вечный двигатель.
Прямоугольник есть геометрическая фигура.
Сегодня великолепная погода.
Каждый человек - художник.
Который час?
Употребляемые в обычной речи слова и словосочетания «не», «и», «или», «если», «то», «тогда и только тогда» и другие позволяют из уже заданных высказываний строить новые высказывания. Такие слова и словосочетания называются логическими связками. Высказывания, образованные из других высказываний с помощью логических связок, называются составными. Высказывания, не являющиеся составными, называются элементарными (простыми).
Слайд 5Определить истинность сложных высказываний:
Суффикс – это часть слова, и он
стоит после корня.
Рыбу ловят сачком, или ловят крючком, или мухой
приманивают, иль червяком.Буква «а» - первая буква в слове «аист» или «сова».
Луна – планета или 2 + 3 = 5
Слайд 6 Логические высказывания принято обозначать буквами английского алфавита: А, В, С,
х, у и т.д.
Истинность высказывания обозначают:
И либо 1.
Ложность высказывания
обозначают: Л либо 0.
Слайд 7Основные логические операции
Существует три основные логические операции: отрицание (операция, выражаемая
словом «не»), дизъюнкция (операция, выражаемая связкой «или») и конъюкция (операция,
выражаемая связкой «и»).
Слайд 8Отрицание (инверсия, не)
Инверсия истинна тогда, когда само высказывание ложно, и
ложно, когда высказывание истинно.
Обозначение:
Таблица истинности:
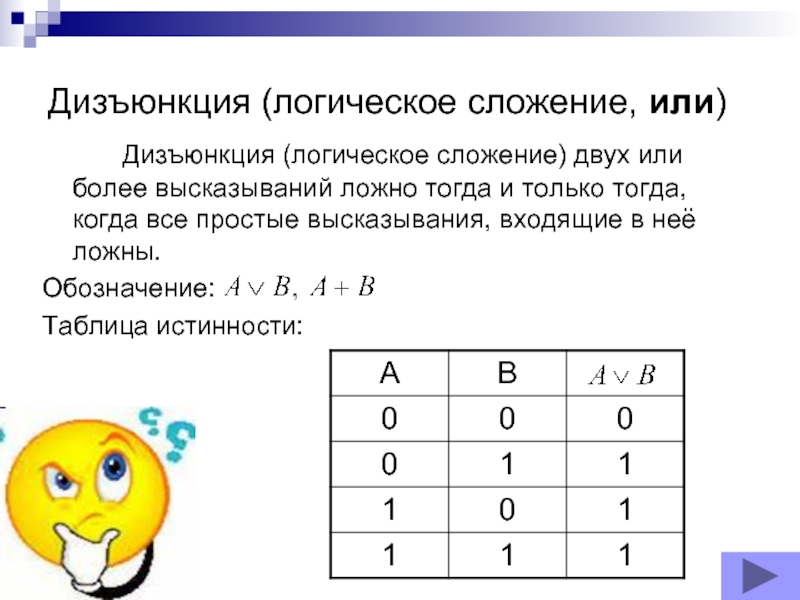
Слайд 9Дизъюнкция (логическое сложение, или)
Дизъюнкция (логическое сложение) двух или более высказываний
ложно тогда и только тогда, когда все простые высказывания, входящие
в неё ложны.Обозначение:
Таблица истинности:
Слайд 10Конъюнкция (логическое умножение, и)
Конъюнкция (логическое умножение) двух и более высказываний
истинно тогда и только тогда, когда все простые высказывания, входящие
в неё истинны.Обозначение:
Таблица истинности:
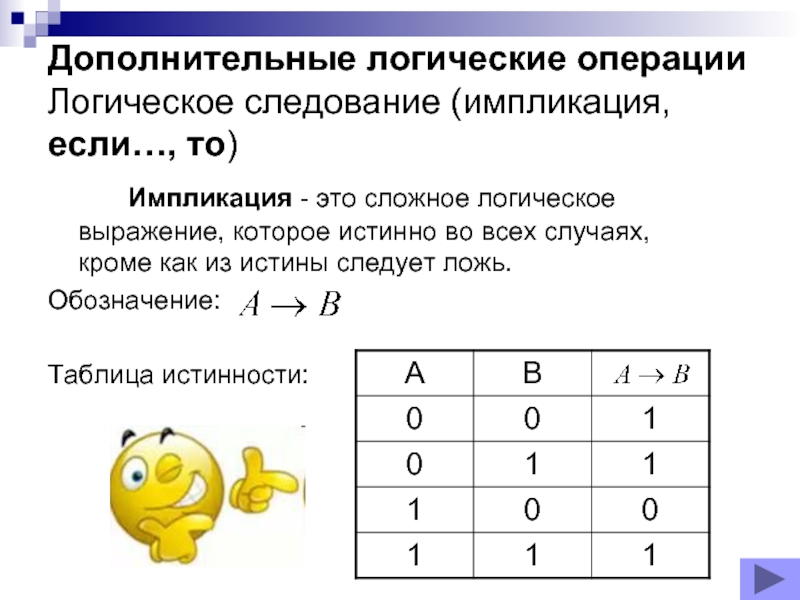
Слайд 14Дополнительные логические операции
Логическое следование (импликация, если…, то)
Импликация - это сложное
логическое выражение, которое истинно во всех случаях, кроме как из
истины следует ложь.Обозначение:
Таблица истинности:
Слайд 15Равнозначность (эквивалентность, тогда и только тогда, когда)
Эквивалентность - это сложное
логическое выражение, которое является истинным тогда и только тогда, когда
оба простых логических выражения имеют одинаковые значения. Обозначение:Таблица истинности:
Слайд 16Порядок выполнения логических операций в сложном логическом выражении
1. Инверсия (не);
2. Конъюнкция (и);
3. Дизъюнкция (или);
4. Импликация (следование);
5.
Эквивалентность (равнозначность). Для изменения указанного порядка выполнения логических операций используются скобки.
Слайд 19Логические основы работы компьютера
Компьютер работает на электричестве, т.е. логические элементы
компьютера оперируют с сигналами, представляющими собой электрические импульсы. Есть импульс
– логический смысл сигнала – 1, нет импульса – 0. На входы логического элемента поступают сигналы-значения аргументов, на выходе появляется сигнал-значение функции.Преобразование сигнала логическим элементом является таблицей состояния, которая фактически является таблицей истинности, соответствующей логической функции.
Базовые логические элементы реализуют рассмотренные выше три основные логические операции
Слайд 20Логический элемент «И»
На выходы А и В логического элемента
подаются два сигнала (00,01,10 или 11). На выходе получается сигнал
0 или 1 в соответствии с таблицей истинности операции логического умножения.
Слайд 21Логический элемент «ИЛИ»
На входы А и В логического элемента подаются
два сигнала (00, 01, 10 или 11). На выходе получается
сигнал 0 или 1 в соответствии с таблицей истинности операции логического сложения.
Слайд 22Логический элемент «НЕ»
На вход А логического элемента подается сигнал 0
или 1. На выходе получается сигнал 0 или 1 в
соответствии с таблицей истинности инверсии.
Слайд 24Законы и тождества алгебры логики
1. Коммутативный закон:
A Λ B = B
Λ A; A ∨ B = B ∨
A.2. Ассоциативный закон:
A Λ (B Λ C) = (A Λ B) Λ C;
A ∨ (B ∨ C) = (A ∨ B) ∨ C.
3. Дистрибутивный закон:
A Λ (B ∨ C) = (A Λ B) ∨ (A Λ C).
A ∨ (B Λ C) = (A ∨ B) Λ (A ∨ C).
Слайд 254. Закон противоречия:
5. Закон исключенного третьего:
6. Закон двойного
отрицания:
7. Законы де Моргана:
Слайд 268. Законы повторения:
A Λ A = A; A v
A = A.
9. Законы исключения констант:
A ∨ 1 =
1; A ∨ 0 = A; A Λ 1 = A; A Λ 0 = 0;
10.
11.
Существует еще несколько логических законов и тождеств, но они достаточно легко выводятся при помощи формул, приведенных выше