Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Программирование на языке Си
Содержание
- 1. Программирование на языке Си
- 2. Структурное программирование на языке СиТема 1. Теория© К.Ю. Поляков, 2007-2009
- 3. Этапы разработки программПостановка задачиопределить цель и категорию
- 4. Этапы разработки программРазработка модели данныхформальная модельтипы данных
- 5. Этапы разработки программТестирование программы (проверка на исходных
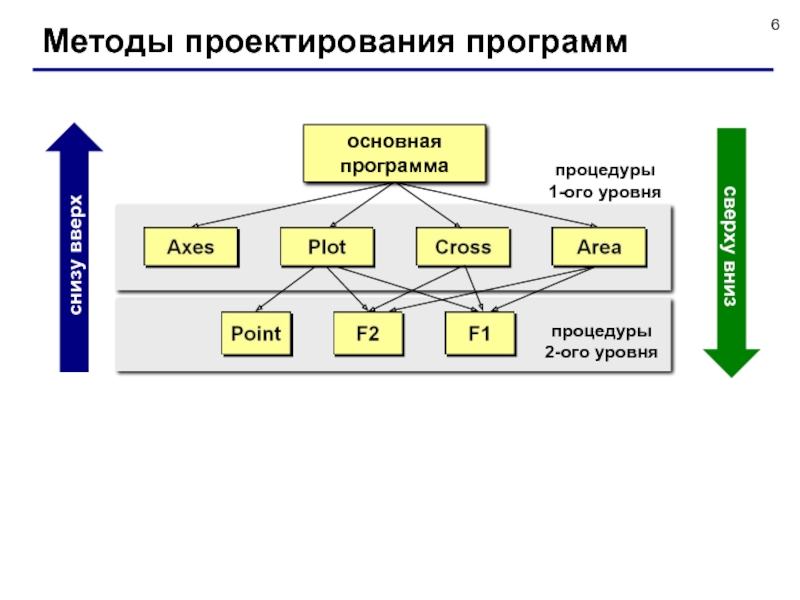
- 6. Методы проектирования программосновная программапроцедуры 1-ого уровняпроцедуры 2-ого уровняснизу вверхсверху вниз
- 7. Проектирование «снизу вверх»сначала составляются процедуры нижнего уровня,
- 8. Проектирование «сверху вниз»метод последовательного уточнения: начинаем с
- 9. Структурное программированиеСуществовавшие проблемы: увеличилась сложность программсократилось время
- 10. Структурное программированиеПринципы: абстракции: программу можно рассматривать на
- 11. МодульМодуль – это программный блок (процедура или
- 12. Оформление текста программыШапка – комментарий в начале
- 13. Оформление текста программыОтступы – тело цикла, условного
- 14. Оформление текста программы«говорящие» имена функций, процедур, переменных:
- 15. Структурное программирование на языке СиТема 2. Проект© К.Ю. Поляков, 2007-2009
- 16. Проект «Графики функций»построить координатные оси и
- 17. Проект «Графики функций»найти точки пересечения графиков, используя численные методызаштриховать образованную замкнутую областьx=3,58y=2,14x=1,40y=1,55
- 18. Проект «Графики функций»вычислить площадь этой области двумя способами оформить отчет по работе S1=3,014S2=3,025
- 19. Структура программы#include#include#include#includemain(){ initwindow(800,600); getch(); closegraph(); }глобальные константы и переменныепроцедуры и функцииосновная программа
- 20. Разбивка программы на этапы Axes(); // оси
- 21. Структурное программирование на языке СиТема 3. Графики функций© К.Ю. Поляков, 2007-2009
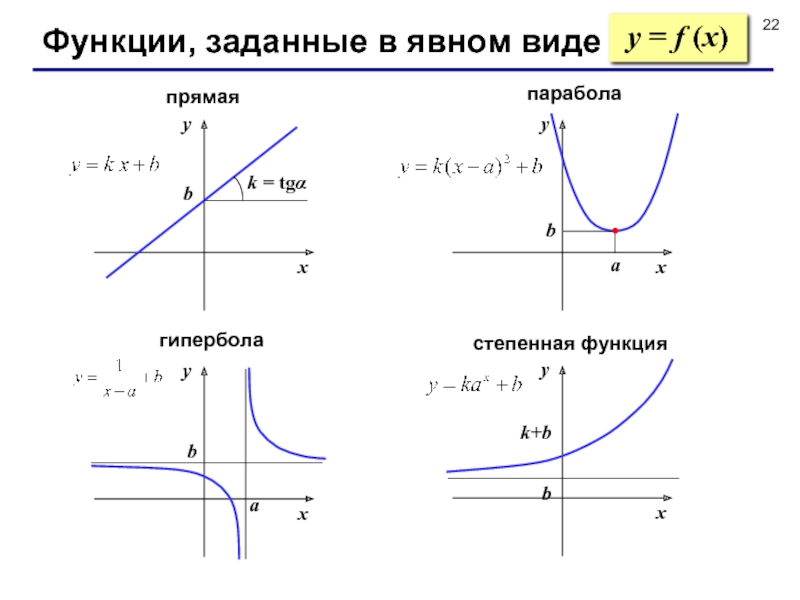
- 22. Функции, заданные в явном видеy = f (x)
- 23. Функции, заданные в неявном видеf (x, y) = 0пример: уравнение эллипса
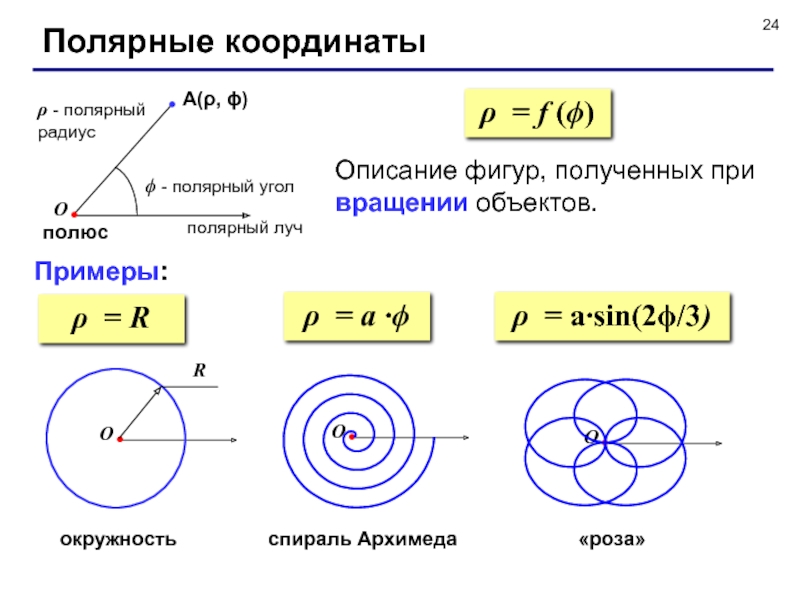
- 24. полюсПолярные координатыА(ρ, ϕ)ϕ - полярный уголρ -
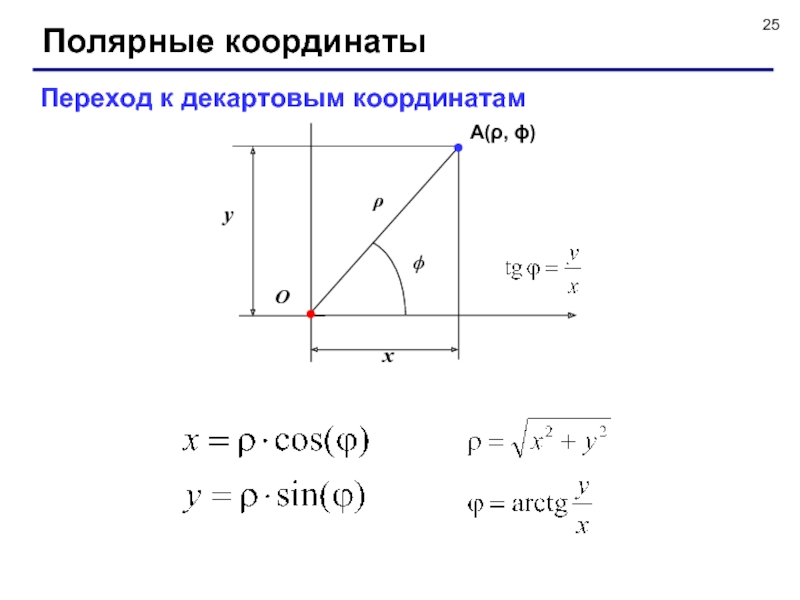
- 25. Полярные координатыПереход к декартовым координатам
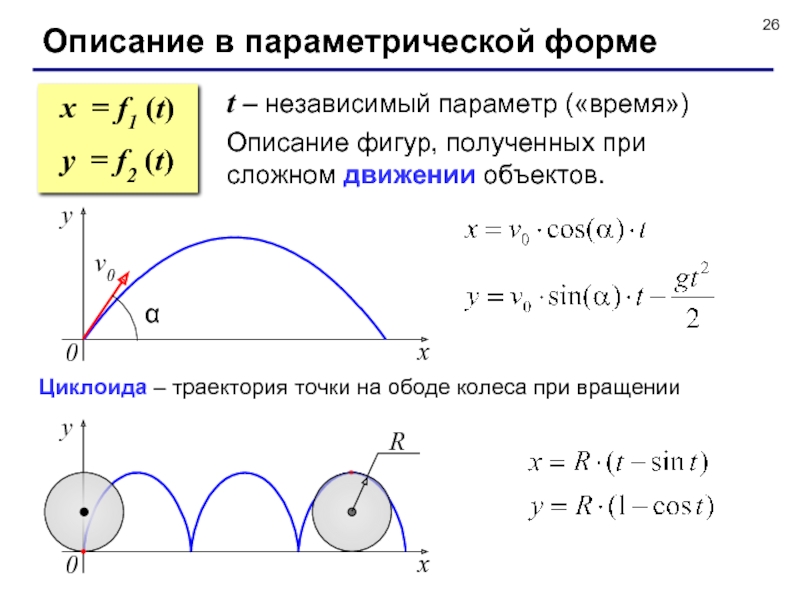
- 26. Описание в параметрической формеt – независимый параметр
- 27. Системы координатМатематическаяЭкраннаяПреобразование координат:X0, Y0 – экранные координаты
- 28. Структура программы#include#include#include#includeconst int X0 = 100, Y0
- 29. Перевод в экранные координаты//-----------------------------------------// SCREENX – перевод
- 30. Оси координатvoid Axes(){ line ( X0, 0,
- 31. Разметка оси X («черточки»)(xЭ, Y0−2)(xЭ, Y0+2)Число меток
- 32. Разметка оси X (числа)1xЭ(xЭ, Y0+2)Вывод символьной строки
- 33. Оси с разметкой (полностью)void Axes(){ int i,
- 34. Задания«4»: Сделать разметку осей полностью (не только
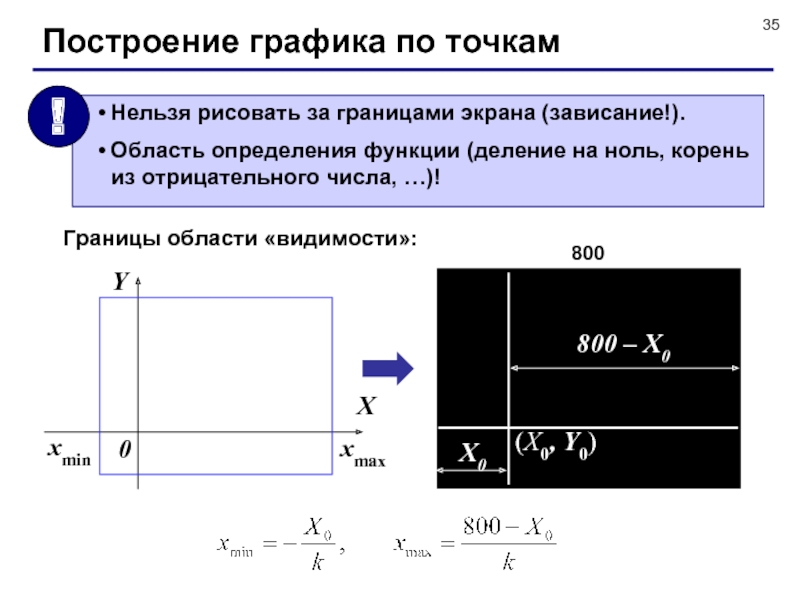
- 35. Построение графика по точкамГраницы области «видимости»:
- 36. Вывод точки с проверкой//----------------------------------------// POINT вывод пикселя
- 37. Описание функций//-----------------------------------------// F1, F2// Вход: x
- 38. Области определения//----------------------------------------// ODZ1 – область определения f1(x)//
- 39. Вывод графика функции//----------------------------------------// PLOT вывод графиков функций//----------------------------------------void
- 40. Общее расположениеfloat f1 ( float x )
- 41. Задания«4»: Построить графики в соответствии с заданием.«5»: Построить графики, соединив точки линиями.
- 42. Структурное программирование на языке СиТема 4. Точки пересечения© К.Ю. Поляков, 2007-2009
- 43. Точки пересеченияf1 (x*) = f2 (x*)abf1 (x*)
- 44. Методы решения уравненийf (x) = 0Точные (аналитические)
- 45. Численные методыПрименение: используются тогда, когда точное (аналитическое)
- 46. Метод прямого («тупого») перебораЗадача: найти решение уравнения
- 47. Есть ли решение на [a, b]?есть решениенет решениянет решения
- 48. Метод дихотомии (деление пополам)Найти середину отрезка [a,b]:
- 49. Метод дихотомии (деления пополам)простотаможно получить решение с
- 50. Метод дихотомии (в программе)//----------------------------------------------// Solve находит точку
- 51. Метод дихотомии (в программе)float xc1, xc2;...float Solve
- 52. Структурное программирование на языке СиТема 5. Штриховка© К.Ю. Поляков, 2007-2009
- 53. Штриховка (две функции)xyxс2xс1y = f1 (x)y =
- 54. Штриховка (составная нижняя граница)xyxс3xс1xс2N линийy = f1
- 55. Штриховка (общий случай)float Up ( float x
- 56. Структурное программирование на языке СиТема 6. Вычисление площади© К.Ю. Поляков, 2007-2009
- 57. Метод (левых) прямоугольниковy = f1 (x)y =
- 58. Метод (правых) прямоугольниковxyxс2xс1y = f1 (x)y =
- 59. Метод (средних) прямоугольниковxyxс2xс1y = f1 (x)y =
- 60. Метод трапецийxyxс2xс1y = f1 (x)y = f2
- 61. Метод Монте-КарлоПрименение: вычисление площадей сложных фигур (трудно
- 62. Метод Монте-КарлоВписываем сложную фигуру в другую фигуру,
- 63. Случайное число в заданном интервале//-----------------------------------------// randF –
- 64. Проверка точки (внутри или нет?)//-----------------------------------------// Inside –
- 65. Метод Монте-Карло (реализация)//----------------------------------------------------// Area2 – вычисление площади
- 66. Структурное программирование на языке СиТема 7. Оформление отчета© К.Ю. Поляков, 2007-2009
- 67. Титульный лист
- 68. Графики функций«скриншот» (screenshot) – «снимок» экраначерез Редактор формул (Вставка – Объект – Microsoft Equation)
- 69. Как получить копию экрана?Поменять цвета так, чтобы
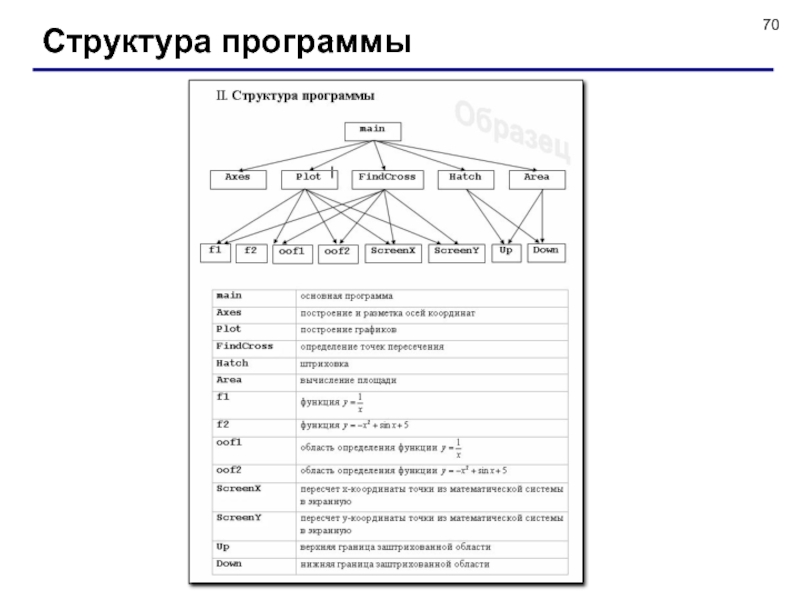
- 70. Структура программы
- 71. Текст программышрифт Courier New,(моноширинный) размер 10 пт
- 72. Конец фильма
- 73. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Структурное программирование
на языке Си
© К.Ю. Поляков, 2007-2009
Теория
Проект
Графики функций
Точки пересечения
Штриховка
Вычисление
площади
Слайд 3Этапы разработки программ
Постановка задачи
определить цель и категорию программы (системная, прикладная)
определить
исходные данные и требуемый результат
проверить, является ли задача хорошо поставленной
(должны быть определены все связи между исходными данными и результатом)
зафиксировать требования к программе в письменной форме
Слайд 4Этапы разработки программ
Разработка модели данных
формальная модель
типы данных (массивы, структуры, …)
взаимосвязь
между данными
Разработка алгоритма
выбор существующего или разработка нового
возможен возврат к шагу
2Разработка программы
Языки: C, C++, Visual Basic, Delphi (Паскаль), `…
Отладка программы (поиск и исправление ошибок) debug – извлечение жучков (bug), 1945, MAРK-I
отладчик (точки останова, пошаговый режим, просмотр переменных)
профайлер (сколько выполняется каждая из процедур)
Слайд 5Этапы разработки программ
Тестирование программы (проверка на исходных данных, для которых
известен результат)
альфа-тестирование: внутри фирмы (тестеры)
бета-тестирование: в других организациях, распространение через
ИнтернетРазработка документации
справочная система
руководство пользователя (User Manual)
руководство разработчика
Сопровождение (техническая поддержка)
исправление ошибок, найденных заказчиком
обучение и консультирование заказчика
новые версии по льготной цене
Слайд 6
Методы проектирования программ
основная
программа
процедуры
1-ого уровня
процедуры
2-ого уровня
снизу вверх
сверху вниз
Слайд 7Проектирование «снизу вверх»
сначала составляются процедуры нижнего уровня, из которых затем
«собираются» процедуры более высокого уровня.
легче начать программировать
более эффективные процедуры
процедуры необходимо
связывать с основной задачей («держать в голове»)при окончательной сборке может не хватить «кубиков»
часто программа получается запутанной
сложно распределить работу в команде
Слайд 8Проектирование «сверху вниз»
метод последовательного уточнения:
начинаем с основной программы;
она разбивается
на подзадачи, для каждой из которых пишется процедура-«заглушка»;
реализуем каждую из
процедур тем же способом.меньше вероятность принципиальной ошибки (начали с главного)
проще структура программы
удобно распределять работу в команде
в разных блоках могут быть реализованы похожие операции (можно было решить одной общей процедурой), особенно в команде
Слайд 9Структурное программирование
Существовавшие проблемы:
увеличилась сложность программ
сократилось время на разработку
Цели:
повысить надежность
уменьшить
время и стоимость разработки
облегчить тестирование и отладку
возможность переделки одного модуля
улучшить
читабельностьбез переходов на другую страницу
избегать трюков и запутанных приемов
Слайд 10Структурное программирование
Принципы:
абстракции: программу можно рассматривать на любом уровне без
лишних подробностей
модульности: программа разбивается на отдельные модули, которые могут отлаживаться
независимо друг от другаподчиненности: связь между модулями «сверху вниз»
локальности: каждый модуль использует только свои локальные переменные, глобальные переменные только в крайних случаях
Слайд 11Модуль
Модуль – это программный блок (процедура или функция), отделенный от
кода других модулей, который полностью решает самостоятельную задачу своего уровня.
работа
модуля не зависит от того, откуда он вызывается, и от того, сколько раз он вызывался до этогоразмер модуля не более 50-60 строк (1 страница)
модуль имеет один вход и один выход
модуль начинается с «шапки»-комментария (входные данные, результаты, какие модули использует)
имена переменных – смысловые
в одной строке – один оператор
«трюки» – долой
Слайд 12Оформление текста программы
Шапка – комментарий в начале процедур и функций.
//----------------------------------------
//
Sum сумма элементов массива
// Вход: A[] – массив целых чисел
//
n - размер массива// Выход: S = A[0]+A[1]+...+A[n-1]
// Вызывает: -
//----------------------------------------
int Sum ( int A[], float n )
{
...
}
Слайд 13
Оформление текста программы
Отступы – тело цикла, условного оператора, оператора выбора
и т.п. сдвигается вправо на 2-3 символа.
for(i=0;i
i++){
j=0;
while ( j < i )
{
j++;
k = k % N;
}
k++;
}
легче читать текст программы
видны блоки
просто найти ошибки со скобками (лишняя, не хватает)
Слайд 14Оформление текста программы
«говорящие» имена функций, процедур, переменных: Sum, ShowMenu, count,
speed.
пробелы в операторах
выделение пустыми
строками и
комментариями
важных блоков
for(i=0;i
i=0; i // ввод данных
printf( "Введите число\n" );
scanf ( "%d", &n );
//вычисления
n2 = n*n;
// вывод результата
printf ( "Его квадрат %d", n2 );
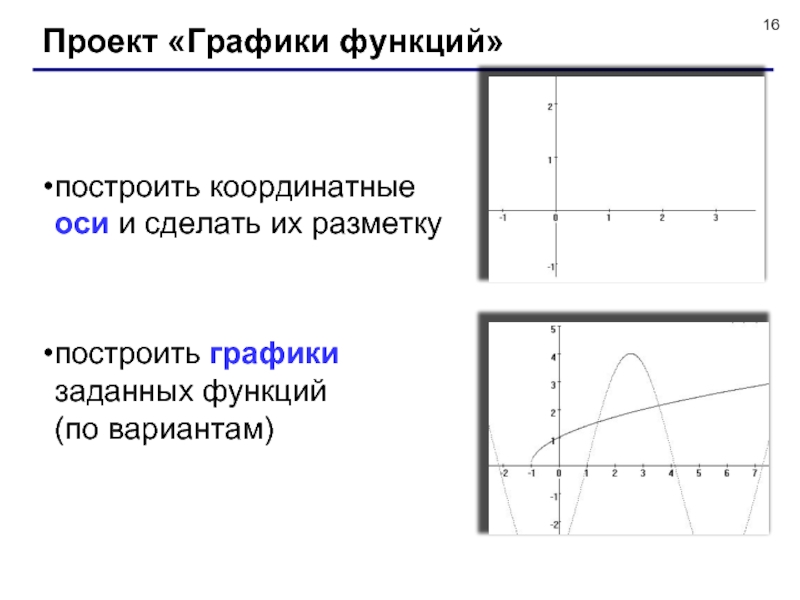
Слайд 16Проект «Графики функций»
построить координатные
оси и сделать их разметку
построить графики
заданных функций
(по вариантам)
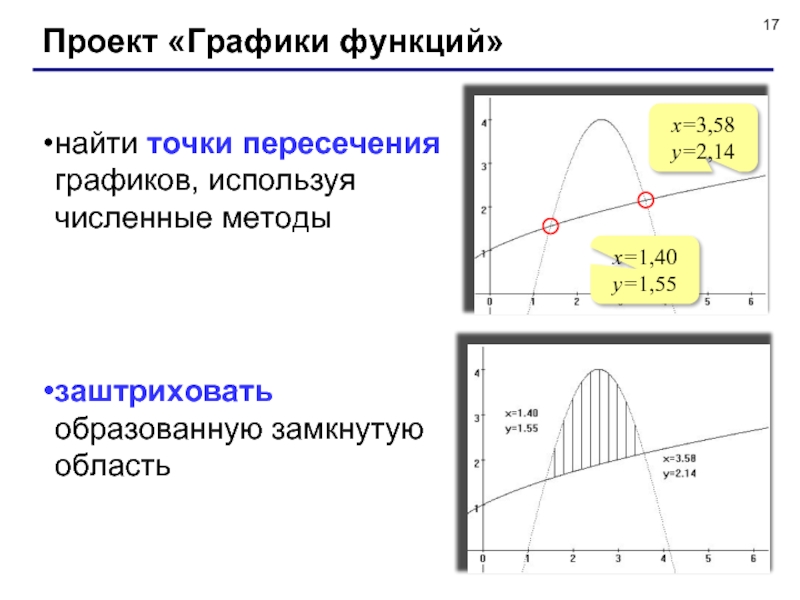
Слайд 17Проект «Графики функций»
найти точки пересечения
графиков, используя
численные методы
заштриховать
образованную
замкнутую
область
x=3,58
y=2,14
x=1,40
y=1,55
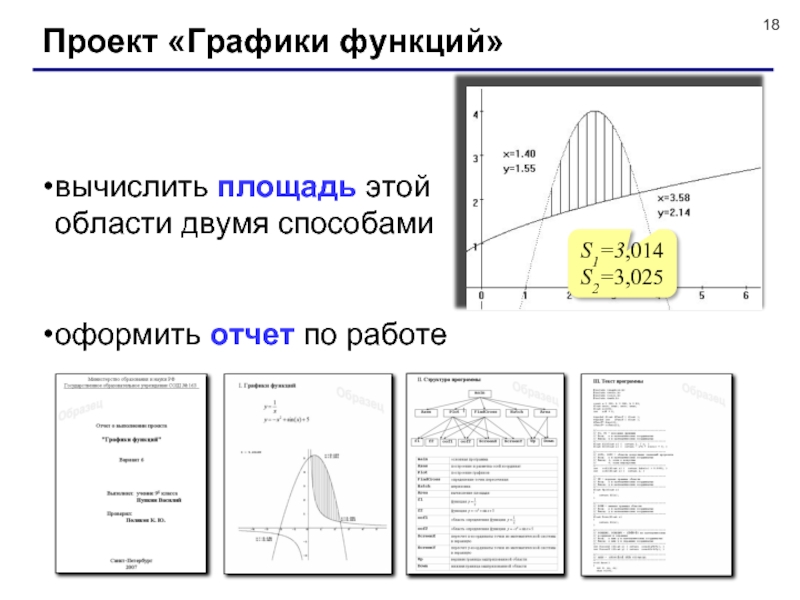
Слайд 18Проект «Графики функций»
вычислить площадь этой
области двумя способами
оформить отчет
по работе
S1=3,014
S2=3,025
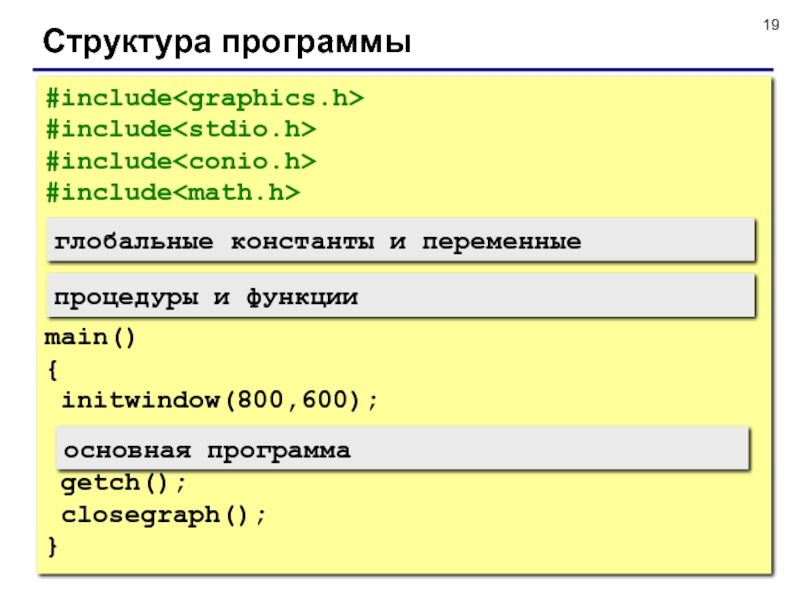
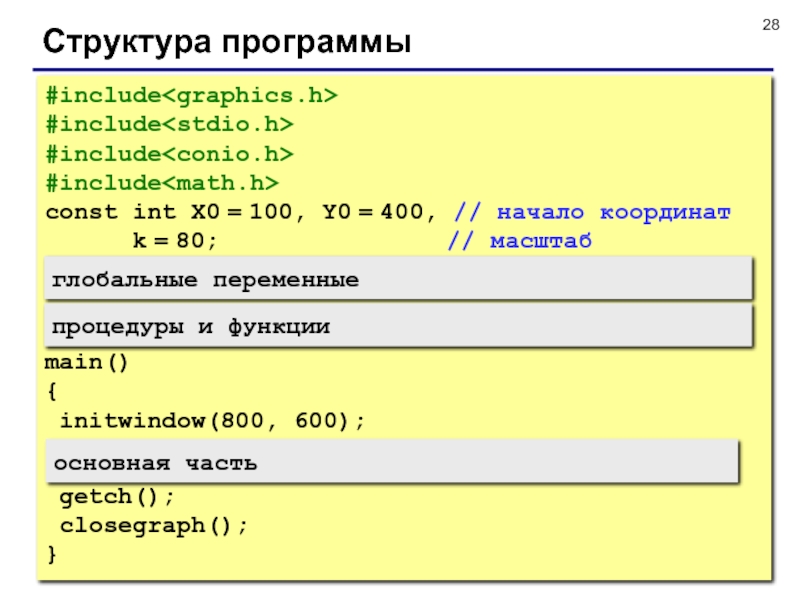
Слайд 19Структура программы
#include
#include
#include
#include
main()
{
initwindow(800,600);
getch();
closegraph();
}
глобальные константы и переменные
процедуры
и функции
основная программа
Слайд 20Разбивка программы на этапы
Axes(); // оси координат
Plot(); //
графики функций
Cross(); // точки пересечения графиков
Hatch(); // штриховка
Area(); // площадь (способ 1)Area2(); // площадь (способ 2)
Основная программа
Процедуры-заглушки
//------------------------------------
// Axes оси координат
//------------------------------------
void Axes()
{
}
Слайд 24полюс
Полярные координаты
А(ρ, ϕ)
ϕ - полярный угол
ρ - полярный радиус
Примеры:
Описание фигур,
полученных при вращении объектов.
ρ = f (ϕ)
ρ = R
окружность
ρ =
a ∙ϕспираль Архимеда
O
O
ρ = a∙sin(2ϕ/3)
«роза»
Слайд 26Описание в параметрической форме
t – независимый параметр («время»)
Описание фигур, полученных
при сложном движении объектов.
x = f1 (t)
y = f2 (t)
Циклоида
– траектория точки на ободе колеса при вращенииR
y
x
0
Слайд 27Системы координат
Математическая
Экранная
Преобразование координат:
X0, Y0 – экранные координаты
точки (0,0)
k –
масштаб (во сколько раз растягивается единичный отрезок)
Слайд 28Структура программы
#include
#include
#include
#include
const int X0 = 100, Y0 = 400, //
начало координат
k = 80;
// масштаб main()
{
initwindow(800, 600);
getch();
closegraph();
}
глобальные переменные
процедуры и функции
основная часть
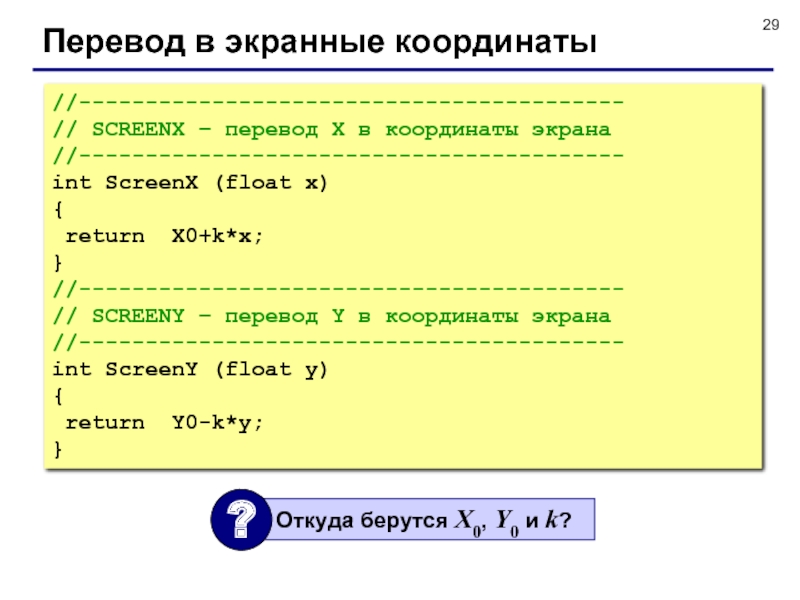
Слайд 29Перевод в экранные координаты
//-----------------------------------------
// SCREENX – перевод X в координаты
экрана
//-----------------------------------------
int ScreenX (float x)
{
return X0+k*x;
}
//-----------------------------------------
// SCREENY
– перевод Y в координаты экрана//-----------------------------------------
int ScreenY (float y)
{
return Y0-k*y;
}
Слайд 31Разметка оси X («черточки»)
(xЭ, Y0−2)
(xЭ, Y0+2)
Число меток на [0, xmax]:
длина 800 – X0
единичный отрезок k
void Axes()
{
int i, xe;...
for (i = 1; i <= (800-X0)/k; i++) {
xe = ScreenX(i);
line ( xe, Y0-2, xe, Y0+2 );
}
}
переходим к экранным координатам
Слайд 32Разметка оси X (числа)
1
xЭ
(xЭ, Y0+2)
Вывод символьной строки в графическом режиме:
outtextxy(x,
y, s);
void Axes()
{
char s[5];
...
for (i = 1;
i <= (800-X0)/k; i++) {...
sprintf ( s, "%d", i );
outtextxy ( xe-4, Y0+3, s );
}
}
координаты левого верхнего угла
(xЭ-4, Y0+3)
8 на 8
перевести целое число i в строку s
строка:
char s[5];
вывести строку s на экран
с запасом…
Слайд 33Оси с разметкой (полностью)
void Axes()
{
int i, xe, ye;
char
s[5];
line ( X0, 0, X0, 599 );
line (
0, Y0, 799, Y0 );for (i = 1; i <= (800-X0)/k; i++)
{
xe = ScreenX(i);
line ( xe, Y0-2, xe, Y0+2 );
sprintf ( s, "%d", i );
outtextxy ( xe-4, Y0+3, s );
}
...
}
Слайд 34
Задания
«4»: Сделать разметку осей полностью (не только положительной части оси
X).
«5»: Сделать задание на «4», использовав только 2 цикла (1
цикл для каждой оси).Слайд 36Вывод точки с проверкой
//----------------------------------------
// POINT вывод пикселя с проверкой и
//
пересчетом координат
//----------------------------------------
void Point ( float x,
float y, int color ){
int xe, ye;
xe = ScreenX(x);
ye = ScreenY(y);
if ( xe >= 0 && xe < 800 &&
ye >= 0 && ye < 600)
putpixel(xe, ye, color);
}
если точка (xЭ, yЭ) в пределах экрана…
координаты в математической системе
цвет точки
Слайд 37Описание функций
//-----------------------------------------
// F1, F2
// Вход: x
// Выход:
y = f(x)
//-----------------------------------------
float f1 ( float x )
{
return
sqrt(x+1); }
float f2 ( float x )
{
return 4*sin(x-1);
}
Слайд 38Области определения
//----------------------------------------
// ODZ1 – область определения f1(x)
// Вход: x
// Выход:
1, если x входит в ОДЗ
// 0,
если x не входит в ОДЗ//----------------------------------------
int odz1 ( float x )
{
return ( x >= -1 );
}
не нужно!
if ( x >= -1 ) return 1;
else return 0;
Слайд 39Вывод графика функции
//----------------------------------------
// PLOT вывод графиков функций
//----------------------------------------
void Plot ()
{
float
xmin = - 1.* X0 / k,
xmax =
(800. - X0) / k;float x,
h = (xmax - xmin) / 1000;
}
чтобы не отбрасывать остаток
границы видимой части
шаг по x
for ( x = xmin; x <= xmax; x += h)
if ( odz1(x) )
Point(x, f1(x), LIGHTRED);
Слайд 40Общее расположение
float f1 ( float x ) { return sqrt(
x + 1 ); }
int odz1 ( float x
) { return x >= -1; }...
void Point(float x, float y, int color)
{
...
}
...
void Plot()
{
...
for ( x = xmin; x <= xmax; x += h)
if ( odz1(x) )
Point(x, f1(x), LIGHTRED);
}
Слайд 41
Задания
«4»: Построить графики в соответствии с заданием.
«5»: Построить графики, соединив
точки линиями.
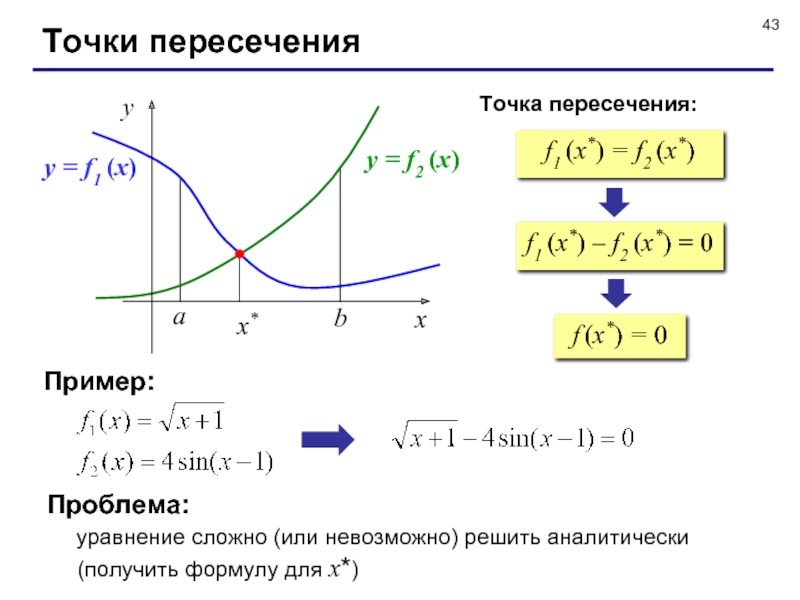
Слайд 43Точки пересечения
f1 (x*) = f2 (x*)
a
b
f1 (x*) – f2 (x*)
= 0
f (x*) = 0
Пример:
Проблема:
уравнение сложно (или невозможно)
решить аналитически
(получить формулу для x*)Точка пересечения:
Слайд 44Методы решения уравнений
f (x) = 0
Точные (аналитические)
Приближенные
графические
численные
(методы последовательного приближения):
по графику
найти интервал [a, b], в котором находится x* (или одно начальное
приближение x0)по некоторому алгоритму уточнить решение, сужая интервал, в котором находится x*
повторять шаг 2, пока не достигнута требуемая точность:
b – a < ε
Слайд 45Численные методы
Применение: используются тогда, когда точное (аналитическое) решение неизвестно или
очень трудоемко.
дают хотя бы какое-то решение
во многих случаях можно оценить
ошибку и найти решение с заданной точностьюрешение всегда приближенное, неточное
Слайд 46Метод прямого («тупого») перебора
Задача: найти решение уравнения f (x) =
0 на интервале [a, b] с заданной точностью ε (чтобы
найденное решение отличалось от истинного не более, чем на ε).Алгоритм:
разбить интервал [a, b] на полосы шириной ε
найти полосу [a*, b*], в которой находится x*
решение – a* или b*
Слайд 48
Метод дихотомии (деление пополам)
Найти середину отрезка [a,b]:
c
= (a + b) / 2;
Если f(c)*f(a)
интервала
b = c;Если f(c)*f(a)≥ 0, сдвинуть левую границу интервала a = c;
Повторять шаги 1-3, пока не будет b – a ≤ ε.
Слайд 49Метод дихотомии (деления пополам)
простота
можно получить решение с любой заданной точностью
нужно
знать интервал [a, b]
на интервале [a, b] должно быть только
одно решениебольшое число шагов для достижения высокой точности
только для функций одной переменной
Слайд 50Метод дихотомии (в программе)
//----------------------------------------------
// Solve находит точку пересечения на [a,b]
//
Вход: a, b – границы интервала, a < b
//
eps - точность решения// Выход: x – решение уравнения f1(x)=f2(x)
//----------------------------------------------
float Solve ( float a, float b, float eps )
{
float c, fa, fc;
while ( b - a > eps )
{
c = (a + b) / 2;
fa = f1(a) - f2(a);
fc = f1(c) - f2(c);
if ( fa*fc < 0 ) b = c;
else a = c;
}
return (a + b) / 2;
}
Слайд 51Метод дихотомии (в программе)
float xc1, xc2;
...
float Solve ( float a,
float b, float eps )
{
...
}
...
void Cross ()
{
char s[20];
sprintf(s, "x=%.2f", xc1);
outtextxy ( 150, 100, s );
sprintf(s, "y=%.2f", f1(xc1));
outtextxy ( 150, 120, s );
...
}
глобальные переменные: абсциссы точек пересечения
найти решение на интервале [1,2] с точностью 0,0001
xc1 = Solve ( 1, 2, 0.0001 );
вывод на экран через символьную строку
… и значение y!
то же самое для остальных точек
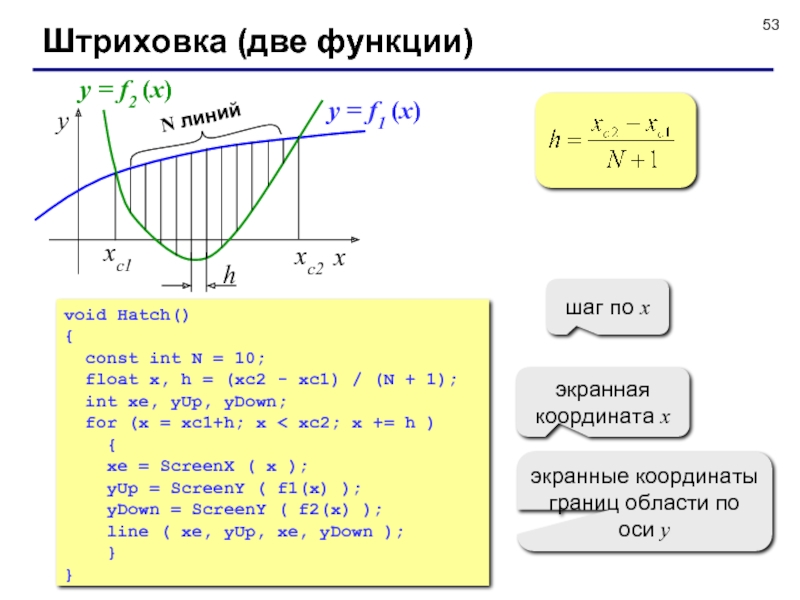
Слайд 53Штриховка (две функции)
x
y
xс2
xс1
y = f1 (x)
y = f2 (x)
void Hatch()
{
const int N = 10;
float x, h = (xc2
- xc1) / (N + 1);int xe, yUp, yDown;
for (x = xc1+h; x < xc2; x += h )
{
xe = ScreenX ( x );
yUp = ScreenY ( f1(x) );
yDown = ScreenY ( f2(x) );
line ( xe, yUp, xe, yDown );
}
}
экранная координата x
экранные координаты границ области по оси y
шаг по x
Слайд 54Штриховка (составная нижняя граница)
x
y
xс3
xс1
xс2
N линий
y = f1 (x)
y = f2
(x)
y = f3 (x)
//----------------------------
// Down нижняя граница области
//----------------------------
float Down (
float x ){
if ( x < xc2 )
return f2(x);
else return f3(x);
}
Слайд 55Штриховка (общий случай)
float Up ( float x ) {
... }
float Down ( float x ) { ...
}...
void Hatch()
{
const N = 10;
float x, h = ( ? ) / (N + 1);
int xe, yUp, yDown;
for ( ? ; x += h )
{
xe = ScreenX ( x );
yUp = ScreenY ( ? );
yDown = ScreenY ( ? );
line ( xe, yUp, xe, yDown );
}
}
xc3 - xc1
x = xc1+h; x < xc3;
Up(x)
Down(x)
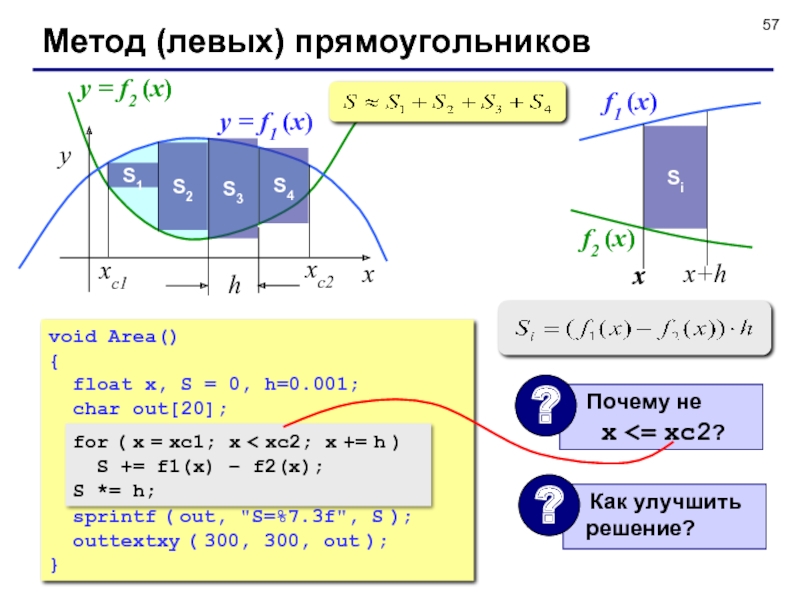
Слайд 57Метод (левых) прямоугольников
y = f1 (x)
y = f2 (x)
S1
S2
S3
S4
void Area()
{
float x, S = 0, h=0.001;
char out[20];
for (
x = xc1; x < xc2; x += h)S += h*(f1(x) – f2(x));
sprintf ( out, "S=%7.3f", S );
outtextxy ( 300, 300, out );
}
for ( x = xc1; x < xc2; x += h )
S += f1(x) – f2(x);
S *= h;
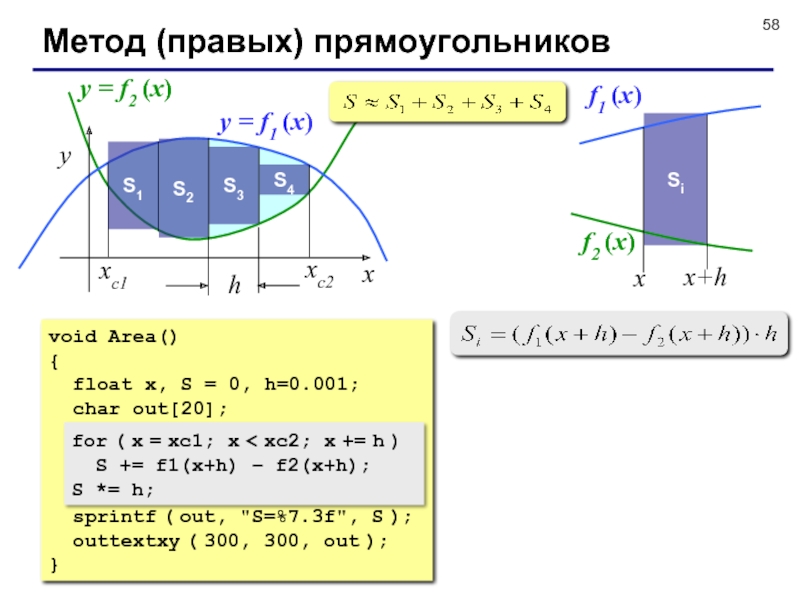
Слайд 58Метод (правых) прямоугольников
x
y
xс2
xс1
y = f1 (x)
y = f2 (x)
S1
S2
S3
S4
void Area()
{
float x, S = 0, h=0.001;
char out[20];
for (
x = xc1; x < xc2; x += h)S += h*(f1(x+h) – f2(x+h));
sprintf ( out, "S=%7.3f", S );
outtextxy ( 300, 300, out );
}
for ( x = xc1; x < xc2; x += h )
S += f1(x+h) – f2(x+h);
S *= h;
Слайд 59Метод (средних) прямоугольников
x
y
xс2
xс1
y = f1 (x)
y = f2 (x)
S1
S2
S3
S4
void Area()
{
float x, S = 0, h=0.001;
char out[20];
for (
x = xc1; x < xc2; x += h)S += h*(f1(x+h) – f2(x+h));
sprintf ( out, "S=%7.3f", S );
outtextxy ( 300, 300, out );
}
for ( x = xc1; x < xc2; x += h )
S += f1(x+h/2) – f2(x+h/2);
S *= h;
левые (правые):
средние
Слайд 60Метод трапеций
x
y
xс2
xс1
y = f1 (x)
y = f2 (x)
for ( x
= xc1; x < xc2; x += h )
S += f1(x) – f2(x) +f1(x+h) – f2(x+h);
S *= h/2;
S =( f1(xc1) - f2(xc1)
+ f1(xc2) - f2(xc2) )/2.;
for ( x = xc1+h; x < xc2; x += h )
S += f1(x) – f2(x);
S *= h;
Слайд 61Метод Монте-Карло
Применение: вычисление площадей сложных фигур (трудно применить другие методы).
Требования:
необходимо уметь достаточно просто определять, попала ли точка (x, y)
внутрь фигуры.Пример: заданы 100 кругов (координаты центра, радиусы), которые могу пересекаться. Найти площадь области, перекрытой кругами.
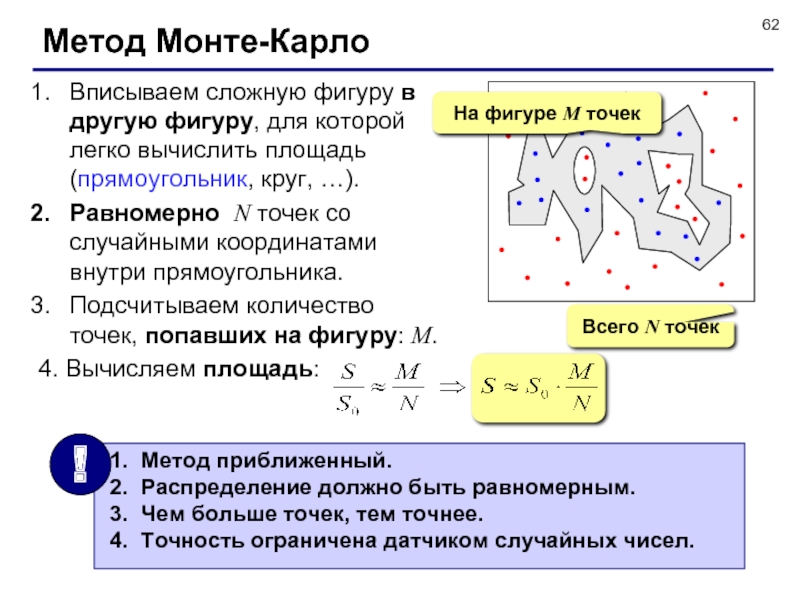
Слайд 62Метод Монте-Карло
Вписываем сложную фигуру в другую фигуру, для которой легко
вычислить площадь (прямоугольник, круг, …).
Равномерно N точек со случайными
координатами внутри прямоугольника. Подсчитываем количество точек, попавших на фигуру: M.
4. Вычисляем площадь:
Всего N точек
На фигуре M точек
Метод приближенный.
Распределение должно быть равномерным.
Чем больше точек, тем точнее.
Точность ограничена датчиком случайных чисел.
!
Слайд 63Случайное число в заданном интервале
//-----------------------------------------
// randF – случайное вещественное число
// в заданном интервале
//-----------------------------------------
float randF (
float a, float b){
return (b-a)*rand() / RAND_MAX + a;
}
rand()
rand()/RAND_MAX
1.*rand()/RAND_MAX
1.*rand()/RAND_MAX + a
(b-a)*rand()/RAND_MAX + a
целое [0, RAND_MAX]
всегда 0!!!
[0,1]
[a,a+1]
[a,b]
Слайд 64Проверка точки (внутри или нет?)
//-----------------------------------------
// Inside – определяет, находится ли
точка
// внутри фигуры
// Вход: x, y
– координаты точки// Выход: 1, если точка внутри фигуры,
// 0, если точка вне фигуры
//-----------------------------------------
int Inside ( float x, float y )
{
if ( Down(x) <= y && y <= Up(x) )
return 1;
else return 0;
}
int Inside ( float x, float y )
{
return (Down(x) <= y && y <= Up(x));
}
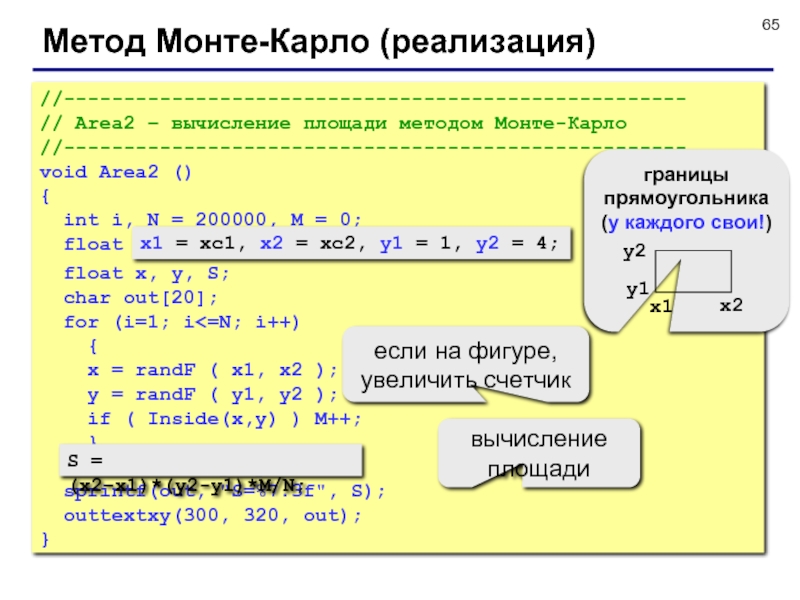
Слайд 65Метод Монте-Карло (реализация)
//----------------------------------------------------
// Area2 – вычисление площади методом Монте-Карло
//----------------------------------------------------
void Area2
()
{
int i, N = 200000, M = 0;
float
float x, y, S;char out[20];
for (i=1; i<=N; i++)
{
x = randF ( x1, x2 );
y = randF ( y1, y2 );
if ( Inside(x,y) ) M++;
}
S = (x2-x1)*(y2-y1)*M/N;
sprintf(out, "S=%7.3f", S);
outtextxy(300, 320, out);
}
x1 = xc1, x2 = xc2, y1 = 1, y2 = 4;
границы прямоугольника (у каждого свои!)
S = (x2-x1)*(y2-y1)*M/N;
вычисление площади
если на фигуре, увеличить счетчик
Слайд 68Графики функций
«скриншот» (screenshot) – «снимок» экрана
через Редактор формул (Вставка –
Объект – Microsoft Equation)
Слайд 69Как получить копию экрана?
Поменять цвета так, чтобы все линии и
текст были белые.
Запустить программу (она должна все нарисовать).
Нажать клавишу PrtScr
(Print Screen – «снимок» экрана) на клавиатуре или комбинацию Alt+PrtScr («снимок» активного окна).В графическом редакторе (Paint): Правка – Вставить.
Перевести в черно-белую палитру (Рисунок – Атрибуты – Палитра – Черно-белая).
Инверсия (черный ↔ белый), Рисунок – Обратить цвета.
Выделить нужную часть рисунка.
Вставить в отчет через буфер обмена (Ctrl+C, Ctrl+V).










![Программирование на языке Си Оформление текста программыШапка – комментарий в начале процедур и функций.//----------------------------------------// Sum Оформление текста программыШапка – комментарий в начале процедур и функций.//----------------------------------------// Sum сумма элементов массива// Вход: A[] –](/img/thumbs/56747d1e60c21a012b73cc2108cdbaaa-800x.jpg)








![Программирование на языке Си Разметка оси X («черточки»)(xЭ, Y0−2)(xЭ, Y0+2)Число меток на [0, xmax]: длина Разметка оси X («черточки»)(xЭ, Y0−2)(xЭ, Y0+2)Число меток на [0, xmax]: длина 800 – X0 единичный](/img/thumbs/93df4adb212de42c43ca8b1e4d9b3ef8-800x.jpg)
![Программирование на языке Си Разметка оси X (числа)1xЭ(xЭ, Y0+2)Вывод символьной строки в графическом режиме:outtextxy(x, y, Разметка оси X (числа)1xЭ(xЭ, Y0+2)Вывод символьной строки в графическом режиме:outtextxy(x, y, s);void Axes(){ char s[5]; ... for](/img/thumbs/1cbc5fff37378d7f4d0d3fa825899475-800x.jpg)
![Программирование на языке Си Оси с разметкой (полностью)void Axes(){ int i, xe, ye; char s[5]; Оси с разметкой (полностью)void Axes(){ int i, xe, ye; char s[5]; line ( X0, 0, X0, 599](/img/thumbs/79e673ec94a652b54de76cdc67cc8501-800x.jpg)








![Программирование на языке Си Методы решения уравненийf (x) = 0Точные (аналитические) Приближенныеграфическиечисленные (методы последовательного приближения):по Методы решения уравненийf (x) = 0Точные (аналитические) Приближенныеграфическиечисленные (методы последовательного приближения):по графику найти интервал [a, b], в](/img/thumbs/8aa0e9ddd53de27fba94c1722240a2fb-800x.jpg)

![Программирование на языке Си Метод прямого («тупого») перебораЗадача: найти решение уравнения f (x) = 0 Метод прямого («тупого») перебораЗадача: найти решение уравнения f (x) = 0 на интервале [a, b] с заданной](/img/thumbs/66fb5411740e0e5ed7c710434ce6b5e0-800x.jpg)
![Программирование на языке Си Есть ли решение на [a, b]?есть решениенет решениянет решения Есть ли решение на [a, b]?есть решениенет решениянет решения](/img/thumbs/0da2d0dd55fa7fbf2203f110ba34e39a-800x.jpg)
![Программирование на языке Си Метод дихотомии (деление пополам)Найти середину отрезка [a,b]: c = (a + b) / 2;Если f(c)*f(a) Метод дихотомии (деление пополам)Найти середину отрезка [a,b]: c = (a + b) / 2;Если](/img/thumbs/bd5a1aa1732c59b1bc17acdc1ce4b159-800x.jpg)
![Программирование на языке Си Метод дихотомии (деления пополам)простотаможно получить решение с любой заданной точностьюнужно знать Метод дихотомии (деления пополам)простотаможно получить решение с любой заданной точностьюнужно знать интервал [a, b]на интервале [a, b]](/img/thumbs/bd6419ffb69ade252a566a7a962aa05b-800x.jpg)
![Программирование на языке Си Метод дихотомии (в программе)//----------------------------------------------// Solve находит точку пересечения на [a,b]// Вход: Метод дихотомии (в программе)//----------------------------------------------// Solve находит точку пересечения на [a,b]// Вход: a, b – границы интервала, a](/img/thumbs/eb90e2bf17938d92a4508f68fd585d46-800x.jpg)