Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Сиcтемы счисления
Содержание
- 1. Сиcтемы счисления
- 2. Система счисления - способ записи чисел, с помощью заданного набора цифр, символов?
- 3. Системы счисления делятся на два класса:ПОЗИЦИОННЫЕНЕПОЗИЦИОННЫЕ
- 4. НЕПОЗИЦИОННАЯ СИСТЕМА СЧИСЛЕНИЯ Система счисления,
- 5. Запомните особенность римской записи: меньшая цифра, стоящая
- 6. Позиционная система счисления – система счисления, в
- 7. S – основание системы счисленияЛюбое число в
- 8. Количество цифр, используемых для записи числа в
- 9. Десятичная система счисления:Пришла в Европу из Индии,
- 10. Десятичная система счисленияНабор цифр, используемых для записи
- 11. Двоичная система счисления:В этой системе используются две
- 12. Двоичная система счисленияНабор цифр, используемых для записи
- 13. В этой системе счисления 8 цифр: 0,
- 14. Восьмеричная система счисленияНабор цифр, используемых для записи
- 15. Запись числа в восьмеричной системе счисления достаточно
- 16. Шестнадцатиричная система счисленияПример: F5(16)=15*161 +5*160 =
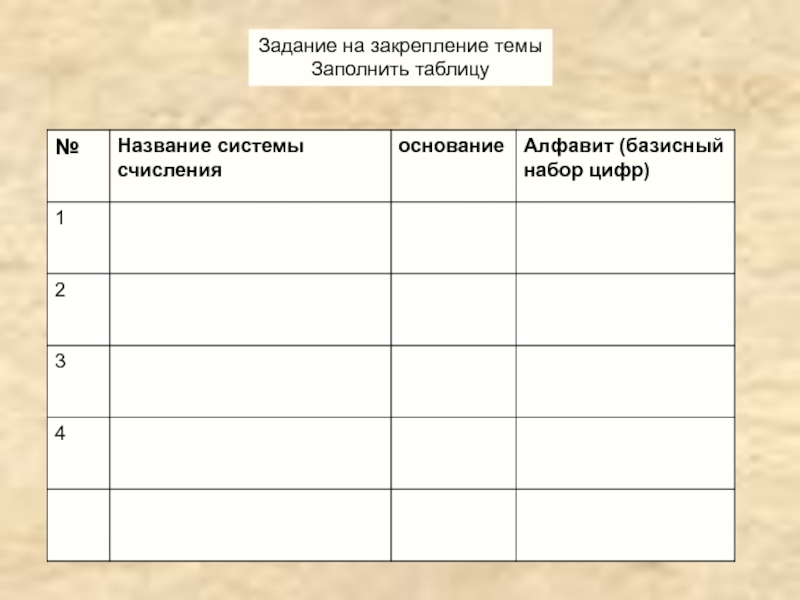
- 17. Задание на закрепление темыЗаполнить таблицу
- 18. Арифметические действиянад двоичными числами
- 19. Слайд 19
- 20. Слайд 20
- 21. Слайд 21
- 22. Перевод чисел в различные системы счисления.
- 23. Перевод чисел из десятичной системы счисления в любую другую
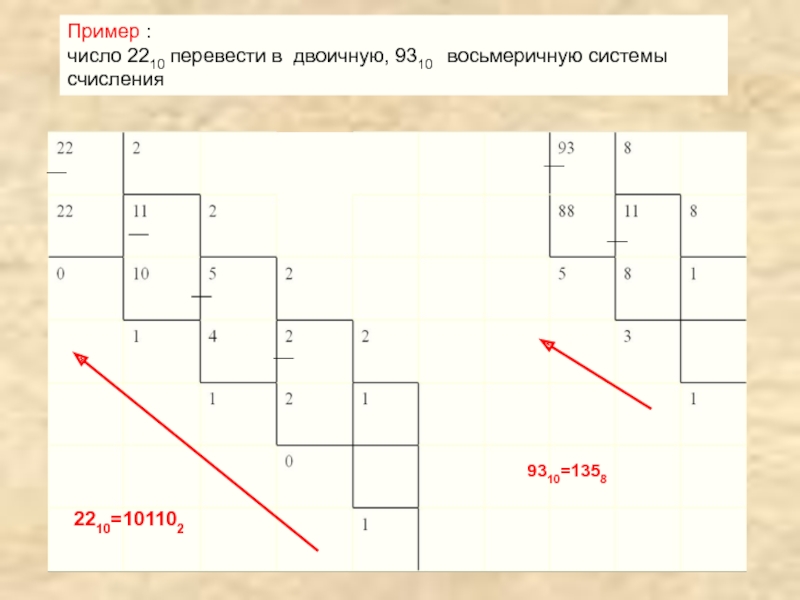
- 24. Пример : число 2210 перевести в двоичную, 9310 восьмеричную системы счисления
- 25. Перевод чисел в десятичную систему счисления
- 26. 3 2 1 012378
- 27. ТриадыТетрдыТаблица для перевода двоичных чисел в 8- ричную, 16 – ричную системы счисления и обратно
- 28. Слайд 28
- 29. Перевод двоичного числа в шестнадцатеричную систему счисления.ПРАВИЛОДля
- 30. Слайд 30
- 31. Скачать презентанцию
Слайды и текст этой презентации
Слайд 4НЕПОЗИЦИОННАЯ СИСТЕМА СЧИСЛЕНИЯ
Система счисления, в которой значение
символа
не зависит
от его положения в заданном числе.Рассмотрим РИМСКУЮ СИСТЕМУ СЧИСЛЕНИЯ
Слайд 5Запомните особенность римской записи: меньшая цифра, стоящая справа от большей,
прибавляется к ней, стоящая слева - отнимается. Поэтому знак VI
означает 5+1, то есть 6, а знак IV -5-1, то есть 4. Научиться читать числа, записанные в римской нумерации, нетрудно. Позднее появились значки и для обозначения других чисел. Так 100 стали обозначать буквой С (первая буква соответствующего латинского слова - centum), число 1000 - буквой М (mille - тысяча), число 500 - буквой D, буквой L - число 50.В позднейшем своем виде римские цифры выглядят так:
I = 1
V = 5
X = 10
L = 50
C = 100
D= 500
M = 1000
Примеры чисел :
31 – ХХХI
99 – IC
46 – XLVI
1989 – MCMLXXXIX
M – 1000
CM – 900
LXXX – 80
IX - 9
Слайд 6Позиционная система счисления – система счисления, в которой количественное значение(вес)
цифры зависит от его позиции в данном числе.
Позиции цифры называют
разрядом . Разряд числа возрастает справа налево.В позиционных системах счисления вес каждой цифры изменяется в зависимости от ее позиции в последовательности цифр, изображающих число.
?
Слайд 7
S – основание системы счисления
Любое число в позиционной системе счисления
с произвольным основанием(S) , можно представить в виде суммы степеней
основания(S)?
Слайд 8
Количество цифр, используемых для записи числа в позиционной системе счисления
называется основанием.
Основание показывает во сколько раз различаются значения цифр соседних
разрядов чисел.Наиболее распространенной в настоящее время являются десятичная, двоичная, восьмеричная и шестнадцатиричная позиционные системы счисления.
?
Слайд 9Десятичная система счисления:
Пришла в Европу из Индии, где она появилась
не позднее VI века н.э. В этой системе 10 цифр:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, но информацию несет не только цифра, но и место, на котором цифра стоит (то есть ее позиция). В десятичной системе счисления особую роль играют число 10 - основание системы, и его степени: 10, 100, 1000 и т.д. Самая правая цифра числа показывает число единиц, вторая справа - число десятков, следующая - число сотен и т.д.В современном русском языке, а также в языках других народов названия всех чисел до миллиона составляются из 37 слов, обозначающих числа 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 , 12, 13, 14, 15, 16, 17, 18, 19, 20, 30, 40, 50, 60, 70, 80, 90, 100, 200, 300, 400, 500, 600, 700, 800, 900, 1000 (например, восемьсот пятнадцать тысяч триста девяносто четыре). В свою очередь названия этих 37 чисел, как правило, образованы из названий чисел первого десятка (1, 2, 3, 4, 5, 6, 7, 8, 9) и чисел 10, 100, 1000 (например, 18 = восемь на десять, 30 = тридесять и т.д.). В основе этого словообразования лежит число десять, и поэтому наша система наименований называется десятичной системой счисления.
Десятичная система счисления
Слайд 10Десятичная система счисления
Набор цифр, используемых для записи чисел
Алфавит : 0,
1, 2, 3, 4, 5, 6, 7, 8, 9
Пример:
1205(10)= 1000+200+0+5 =1*103 + 2*102 +0*101 +5*100 Количество цифр, при помощи которых записываются числа = 10
Основание = 10
?
Слайд 11Двоичная система счисления:
В этой системе используются две цифры - 0
и 1, а также символы «+» и «-» для обозначения
знака числа, «,» для разделения целой и дробной части. Особую роль здесь играет число 2 и его степени: 2, 4, 8 и т.д. Самая правая цифра числа показывает число единиц, следующая цифра - число двоек, следующая - число четверок и т.д. Двоичная система счисления позволяет закодировать любое натуральное число - представить его в виде последовательности нулей и единиц. В двоичном виде можно представлять не только числа, но и любую другую информацию: тексты, картинки, фильмы и аудиозаписи. Инженеров двоичное кодирование привлекает тем, что легко реализуется технически. Например, при подаче сигнала тока возможны 2 случая - есть сигнал (1)Двоичная система счисления
Слайд 12Двоичная система счисления
Набор цифр, используемых для записи чисел
Алфавит
0, 1
Пример: 1101(10)=1*23 + 1*22 +0*21 +1*20 =
8+4+0+1Количество цифр, при помощи которых записываются
числа = 2 Основание = 2
Примеры записи двоичного числа: 11012, 11110112, 102
?
?
Слайд 13
В этой системе счисления 8 цифр: 0, 1, 2, 3,
4, 5, 6, 7. Цифра 1, указанная в самом младшем
разряде, означает - как и в десятичном числе - просто единицу. Та же цифра 1 в следующем разряде означает 8, в следующем 64 и т.д. Число 100 (восьмеричное) есть не что иное, как 64 (десятичное).Восьмеричная система счисления:
Слайд 14Восьмеричная система счисления
Набор цифр, используемых для записи чисел
Алфавит 0,
1, 2, 3, 4, 5, 6, 7
Пример: 1205(8)=1*83
+ 2*82 +0*81 +5*80 = 1*512 + 2*64 + 0*8 + 5*1Количество цифр, при помощи которых записываются числа = 8 Основание = 8
Примеры записи восьмеричного числа: 1378, 405618, 608
?
Слайд 15
Запись числа в восьмеричной системе счисления достаточно компактна, но еще
компактнее она получается в шестнадцатеричной системе. В качестве первых 10
из 16 шестнадцатеричных цифр взяты привычные цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, а вот в качестве остальных 6 цифр используют первые буквы латинского алфавита: A, B, C, D, E, F. Цифра 1, записанная в самом младшем разряде, означат просто единицу. Та же цифра 1 в следующем - 16 (десятичное), в следующем - 256 (десятичное) и т.д. Цифра F, указанная в самом младшем разряде, означает 15 (десятичное).Шестнадцатиричная
Система
счисления:
Слайд 16Шестнадцатиричная система счисления
Пример: F5(16)=15*161 +5*160 = 15*16+5*1
Количество цифр, при
помощи которых записываются числа
= 16 Основание
= 16Примеры записи шестнадцатиричного числа: 1116, A3516, EF16
?
Слайд 25Перевод чисел в десятичную систему счисления
из любой другой
системы счисления
ПРАВИЛО
Для перевода числа из любой позиционной системы счисления в
десятичную достаточно представить число в виде суммы степеней основания системы счисления, выполнить вычисления. Полученное число является десятичным числом. ?
Слайд 263 2 1 0
12378 = 1*83 +2*82
+ 3*81 +7*80 = 512 + 128 +24 =66410
Пример
: Число 1001112 перевести в десятичную систему счисления
Воспользуемся таблицей степеней числа 2
5 4 3 2 1 0
1001112 = 1*25 +0*24 +0*23 + 1*22 + 1*21 + 1*20 =32 + 0 + 0 + 4 + 2 + 1 = 3910
Пример :
Число 12378 перевести в десятичную систему счисления
Воспользуемся таблицей степеней числа 8
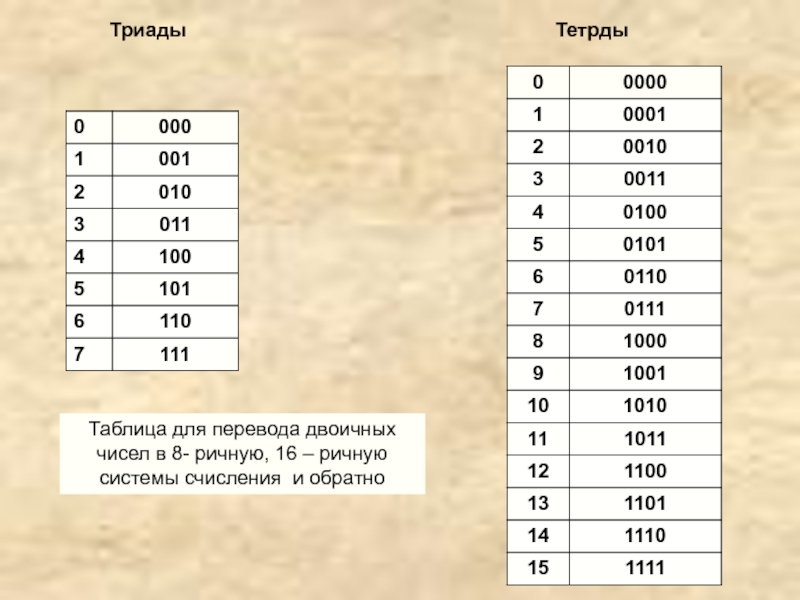
Слайд 27Триады
Тетрды
Таблица для перевода двоичных чисел в 8- ричную, 16 –
ричную системы счисления и обратно
Слайд 28 ?
Перевод двоичного числа
в восьмеричную систему счисления.
Число 10010112 перевести в восьмеричную систему счисления
001 001 0112 = 1138
ПРАВИЛО
Для перевода двоичного числа в восьмеричную систему счисления его нужно разбить на триады (тройки цифр), начиная с младшего разряда, в случае необходимости дополнив старшую триаду нулями, и каждую триаду заменить соответствующей восьмеричной цифрой.
Пример
Слайд 29
Перевод двоичного числа в шестнадцатеричную
систему счисления.
ПРАВИЛО
Для перевода двоичного числа
в шестнадцатеричную систему счисления его нужно разбить на тетрады (четверки
цифр), начиная с младшего разряда, в случае необходимости дополнив старшую тетраду нулями, и каждую тетраду заменить соответствующей шестнадцатеричной цифрой.Число 10111000112 перевести в шестнадцатеричную систему счисления
0010 1110 00112 = 2Е316
Пример
?
Слайд 30 ?
Аpифметические опеpации над
числами в восьмеpичной или шестнадцатеpичной системах пpоводятся по тем же
пpавилам, что и в десятичной системе. Только надо помнить, что если имеет место пеpенос, то пеpеносится не после 10, а 8 или 16.Примеры