Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Свойства логических операций
Содержание
- 1. Свойства логических операций
- 2. Для любых логических формул A, B, C истинны следующие неравенства1. Закон двойного отрицания¬¬A=AДвойное отрицание исключает отрицание.
- 3. Для любых логических формул A, B, C
- 4. Для любых логических формул A, B, C
- 5. Для любых логических формул A, B, C
- 6. Для любых логических формул A, B, C
- 7. Для любых логических формул A, B, C
- 8. Для любых логических формул A, B, C
- 9. Для любых логических формул A, B, C
- 10. Для любых логических формул A, B, C
- 11. для логического сложения: A v (B &
- 12. Умножаем А на (ВvС) и выводим результат.
- 13. Скачать презентанцию
Для любых логических формул A, B, C истинны следующие неравенства1. Закон двойного отрицания¬¬A=AДвойное отрицание исключает отрицание.
Слайды и текст этой презентации
Слайд 3Для любых логических формул A, B, C истинны следующие неравенства
2.
Закон повторения
- для логического умножения
A & A = A
- для логического сложения
A v A = A
Слайд 4Для любых логических формул A, B, C истинны следующие неравенства
3.
Коммутативный (переместительный) закон
- для логического умножения
A & B
= B & A - для логического сложения
A v B = B v A
Слайд 5Для любых логических формул A, B, C истинны следующие неравенства
4.
Ассоциативный (сочетательный) закон
- для логического умножения
(A & B) &
C = A & (B & C)- для логического сложения
(A v B) v C = A v (B v C)
Слайд 6Для любых логических формул A, B, C истинны следующие неравенства
5.
Дистрибутивный (распределительный) закон
- для логического умножения
A & (B v
C) = (A & B) v (A & C)- для логического сложения
A v (B & C) = (A v B) & (A v C)
Слайд 7Для любых логических формул A, B, C истинны следующие неравенства
6.
Законы поглощения
- для логического умножения
A & (A v C)
= A- для логического сложения
A v (A & C) = A
Слайд 8Для любых логических формул A, B, C истинны следующие неравенства
7.
Законы общей инверсии (законы де Моргана)
- для логического умножения
¬(A
& B) = ¬A v ¬B- для логического сложения
¬(A v C) = ¬A & ¬B
Слайд 9Для любых логических формул A, B, C истинны следующие неравенства
8.
Законы исключения третьего
- для логического умножения
A & ¬A =
0- для логического сложения
A v ¬A = 1
Слайд 10Для любых логических формул A, B, C истинны следующие неравенства
9.
Законы операций с 0 и 1
- для логического умножения
A
& 0 = 0; A & 1 = A- для логического сложения
A v 0 = A; A v 1 = 1
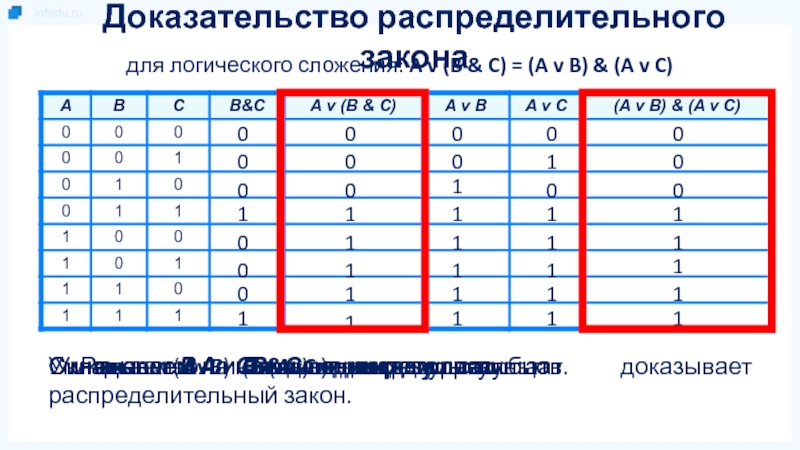
Слайд 11для логического сложения: A v (B & C) = (A
v B) & (A v C)
Доказательство распределительного закона
Умножаем В на
С и выводим результат.0
0
0
0
0
0
1
1
Складываем А и В и выводим результат.
0
0
0
1
1
1
1
1
Складываем А и (В&С) и выводим результат.
0
0
1
1
1
1
1
1
Складываем А и C и выводим результат.
0
0
1
1
1
1
1
1
Умножаем (АvB) на (AvC )и выводим результат.
0
0
0
1
1
1
1
1
Равенство выделенных столбцов доказывает распределительный закон.
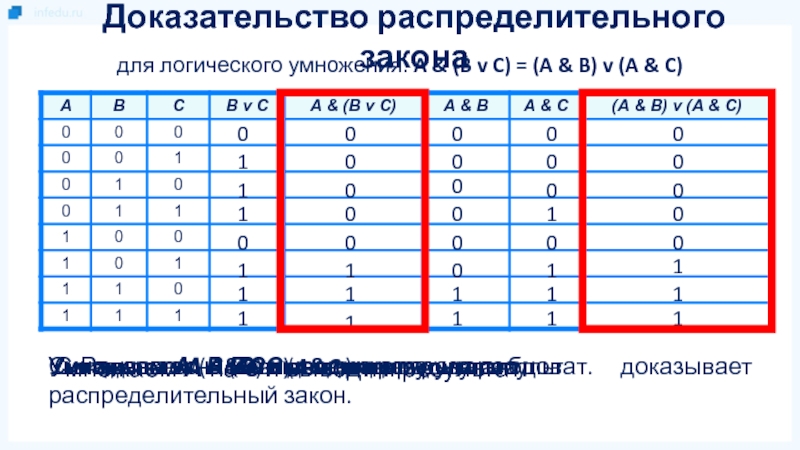
Слайд 12Умножаем А на (ВvС) и выводим результат.
Умножаем А на
C и выводим результат.
Складываем (А&B) и (A&C )и выводим
результат. Равенство выделенных столбцов доказывает распределительный закон.
Умножаем А на В и выводим результат.
для логического умножения: A & (B v C) = (A & B) v (A & C)
Доказательство распределительного закона
Складываем В и С и выводим результат
0
1
1
0
1
1
1
1
0
0
0
0
0
1
1
1
0
0
0
0
0
0
1
1
0
0
0
1
0
1
1
1
0
0
0
0
0
1
1
1
