Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Урок информатики Построение диаграмм по несмежным ячейкам
Содержание
- 1. Урок информатики Построение диаграмм по несмежным ячейкам
- 2. Истинная история человечества – это история науки.
- 3. Число - математическая константаЧисло p
- 4. С чего все начиналось? Открывателями числа можно
- 5. История числа Письменная история числа начинаетсяс
- 6. Обозначение числа Обозначение числа «Пи» происходит от
- 7. Построение диаграммы по несмежным ячейкамДля построения диаграммы
- 8. Вавилон и число Как считают специалисты, это
- 9. «Архимедово число» Идею заменить длину окружности периметром описанного
- 10. Египет (16/9)^2 3,1604 Основание Пирамиды,
- 11. Китай 355/113 3,14159 Примером служит
- 12. Индия √10
- 13. Создание диаграммыВведем все эти данные в различные несмежные ячейки листа Microsoft Excel
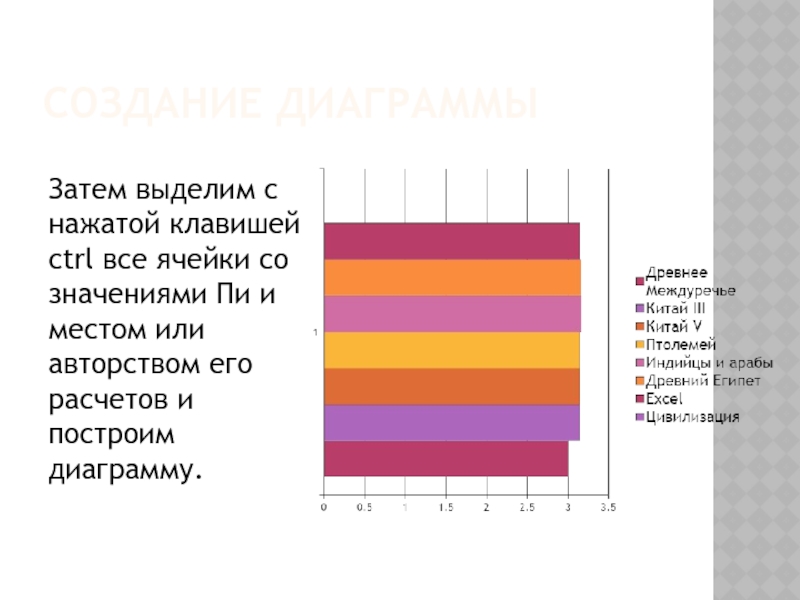
- 14. Создание диаграммыЗатем выделим с нажатой клавишей ctrl
- 15. Компьютер и число 1949 год — 2037
- 16. Применение числа Возможно, что эта математическая константа
- 17. Заключение Число можно вычислять бесконечно, и у
- 18. Скачать презентанцию
Истинная история человечества – это история науки. С. Э. ШнольЦель урока: научиться строить диаграммы по несмежным ячейкам
Слайды и текст этой презентации
Слайд 1Удивительное число
Урок информатики
«Построение диаграмм по несмежным ячейкам»
Материал подготовила
Слайд 2Истинная история человечества – это история науки. С. Э. Шноль
Цель
урока: научиться строить диаграммы по несмежным ячейкам
Слайд 3
Число - математическая константа
Число p - это число, которое
равно отношению длины окружности к ее диаметру.
Слайд 4С чего все начиналось?
Открывателями числа можно считать людей доисторического
времени, которые при плетении корзин заметили, что для того, чтобы
получить корзину нужного диаметра, необходимо брать прутья в 3 раза длиннее его.Найдены таблички из обожженной глины в Месопотамии, на которых зафиксирован данный факт.
Слайд 5История числа
Письменная история числа начинается
с египетского папируса, датируемого
примерно
2000 годом до нашей эры, но
оно было известно ещё
древним людям. Число обратило на себя внимание
людей ещё в те времена, когда они не
умели письменно излагать ни своих
знаний, ни своих переживаний, ни своих
воспоминаний.
Слайд 6Обозначение числа
Обозначение числа «Пи» происходит от греческого слова perijerio
«периферия», что означает «окружность».
Впервые это обозначение использовал в 1706
году английский математик Уильям Джонс, но общепринятым оно стало после того, как его стал систематически употреблять Леонард Эйлер, начиная с 1736 года 
Слайд 7Построение диаграммы по несмежным ячейкам
Для построения диаграммы по несмежным ячейкам,
надо выделять ячейки, нажимая клавишу Ctrl.
Построим диаграмму, показывающую зависимость значения
числа p для разных цивилизаций в истории человечества.
Слайд 8Вавилон и число
Как считают специалисты, это число было открыто
вавилонскими магами Вавилоняне пользовались лишь грубым приближением, определив числом
«3».Число использовалось при строительстве знаменитой Вавилонской башни, но недостаточно точное исчисление значения привело к краху
всего проекта.
Слайд 9«Архимедово число»
Идею заменить длину окружности периметром описанного (вписанного) многоугольника применил
Архимед (III век до н.э.). Начав с 6-угольника, перешел к
12-угольнику, затем к 24-угольнику, и так далее – до 96-угольника. Хорошее приближение оказалось дает число 22/7 3,14286
Слайд 10Египет
(16/9)^2 3,1604
Основание Пирамиды, покоящееся на гранитной поверхности,
представляет собой почти идеальный квадрат (максимальное отклонение 3 минуты 33
секунды) со сторонами около 230 метров.
Слайд 11Китай
355/113 3,14159
Примером служит приближенное вычисление отношения длины окружности
к ее диаметру китайским математиком Цзу Чун-чжи (430-501), который для
получил приближение 355/113.До этого использовали 157/50.
Слайд 12Индия
√10 3,162
Арьябхатта (родился 476
г.н.э.) нашел
точное значение 3,1416 или 62832/20000.
Число 377/120 вычислил Будхайян.
Он
также в 6 веке дал варианты действийтого, что известно как Теорема Пифагора.
Число 3927/1250 вычислил Бхаскара.
Слайд 14Создание диаграммы
Затем выделим с нажатой клавишей ctrl все ячейки со
значениями Пи и местом или авторством его расчетов и построим
диаграмму.
Слайд 15Компьютер и число
1949 год — 2037 десятичных знаков
1958
год — 10000 десятичных знаков
1961 год — 100000 десятичных
знаков1973 год — 10000000 десятичных знаков
1986 год — 29360000 десятичных знаков
1987 год — 134217000 десятичных знаков
1989 год — 1011196691 десятичный знак
1991 год — 2260000000 десятичных знаков
1994 год — 4044000000 десятичных знаков
1995 год — 4294967286 десятичных знаков
1997 год — 51539600000 десятичных знаков
1999 год — 206158430000 десятичных знаков.
Суперкомпьютер в сентябре 1999 года работал 37 часов 21 минут
4 секунды, используя 865 Гбайт памяти для основной задачи,
и 46 часов и 816 Гбайт для вспомогательной оптимизации
вычислений.
Слайд 16Применение числа
Возможно, что эта математическая константа лежала в основе
строительства легендарного Храма царя Соломона.
Астрономия. Космос.
Архитектура. Строительство.
Машиностроение. Навигация. Кораблевождение.
Физика. Электроника.
Электротехника.Информационные технологии. Теория вероятностей.
Слайд 17Заключение
Число можно вычислять бесконечно, и у него будет бесконечно
много знаков.
В настоящее время значение числа известно с точностью
до 500 миллиардов знаков.
