Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Аксиома параллельных прямых
Содержание
- 1. Аксиома параллельных прямых
- 2. Аксиомами называются те основные положения геометрии,
- 3. 1.
- 4. Аксиома параллельных прямых:«Через точку не лежащую на данной прямой, проходит только одна прямая, параллельная данной.»аМв
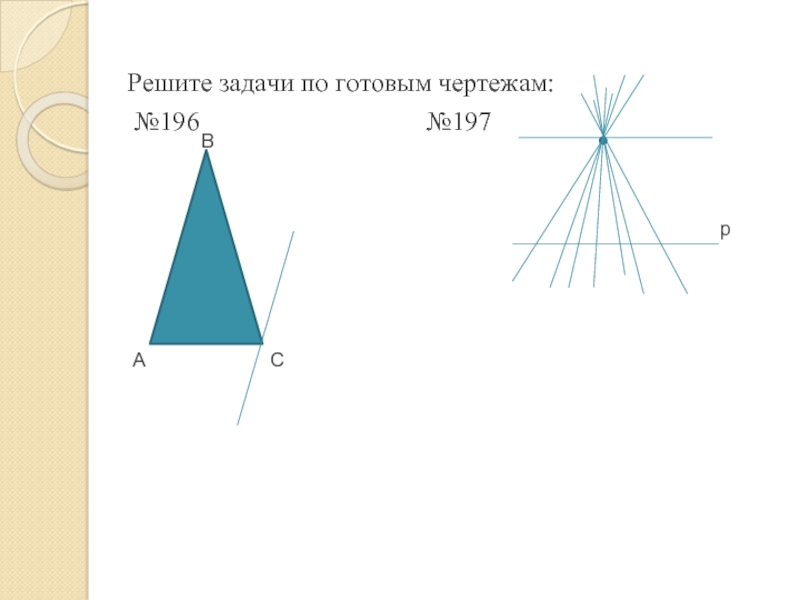
- 5. Решите задачи по готовым чертежам: №196
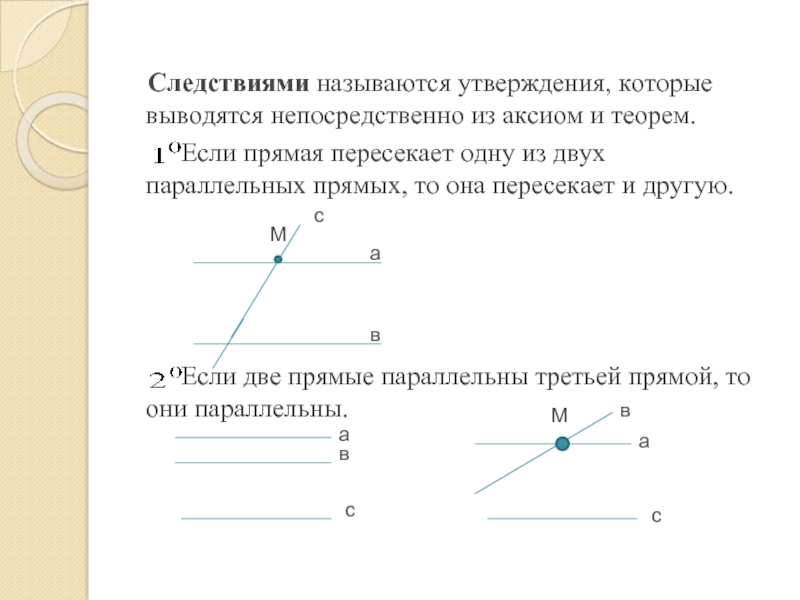
- 6. Следствиями называются утверждения, которые выводятся
- 7. Решить задачи: № 200, 218 Домашнее задание:
- 8. Скачать презентанцию
Аксиомами называются те основные положения геометрии, которые принимаются в качестве исходных положений, на основе которых доказываются далее теоремы и строится вся геометрия.
Слайды и текст этой презентации
Слайд 4 Аксиома параллельных прямых:
«Через точку не лежащую на данной прямой,
проходит только одна прямая, параллельная данной.»
а
М
в
Слайд 6 Следствиями называются утверждения, которые выводятся непосредственно из аксиом
и теорем.
Если прямая пересекает одну
из двух параллельных прямых, то она пересекает и другую. Если две прямые параллельны третьей прямой, то они параллельны.
М
а
в
с
а
в
с
в
а
с
Теги