Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Барицентрический метод решения геометрических задач (центр масс)
Содержание
- 1. Барицентрический метод решения геометрических задач (центр масс)
- 2. Возьмем в пространстве несколько шариков Эту конструкцию
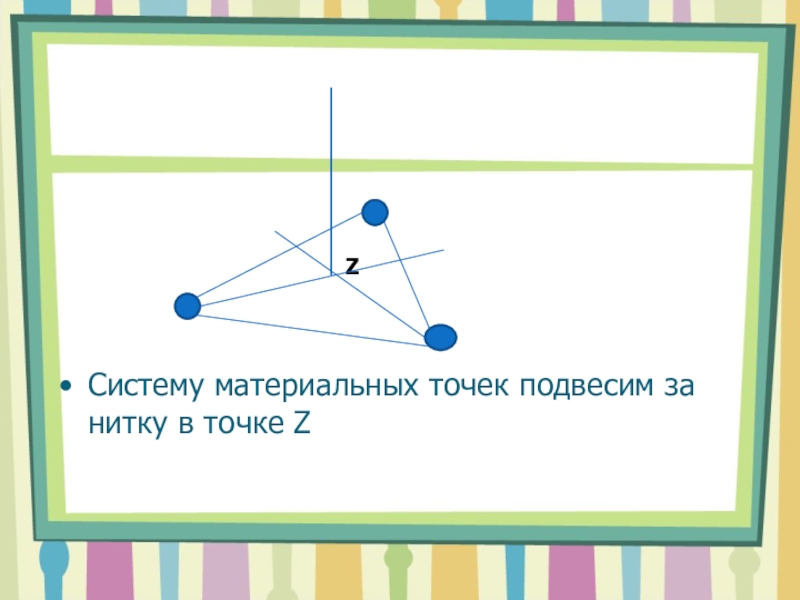
- 3. Систему материальных точек подвесим за нитку в точке ZZ
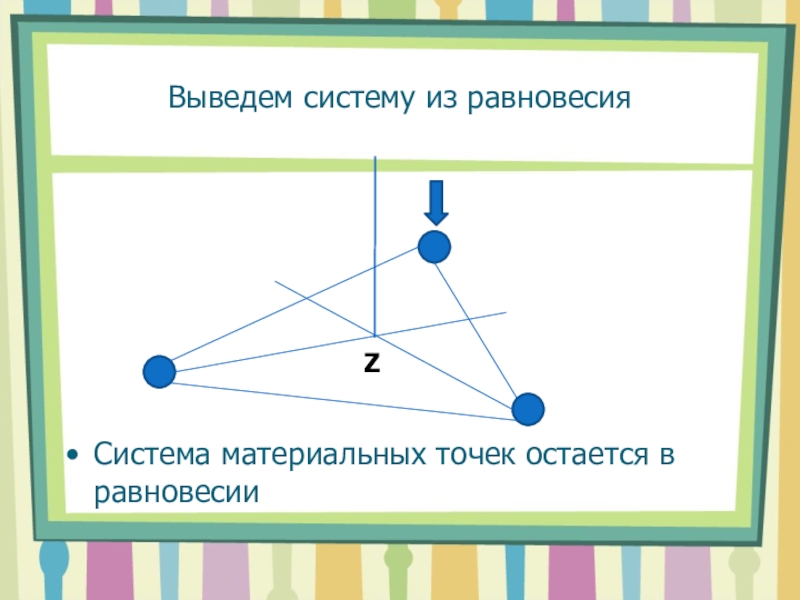
- 4. Выведем систему из равновесияСистема материальных точек остается в равновесииZ
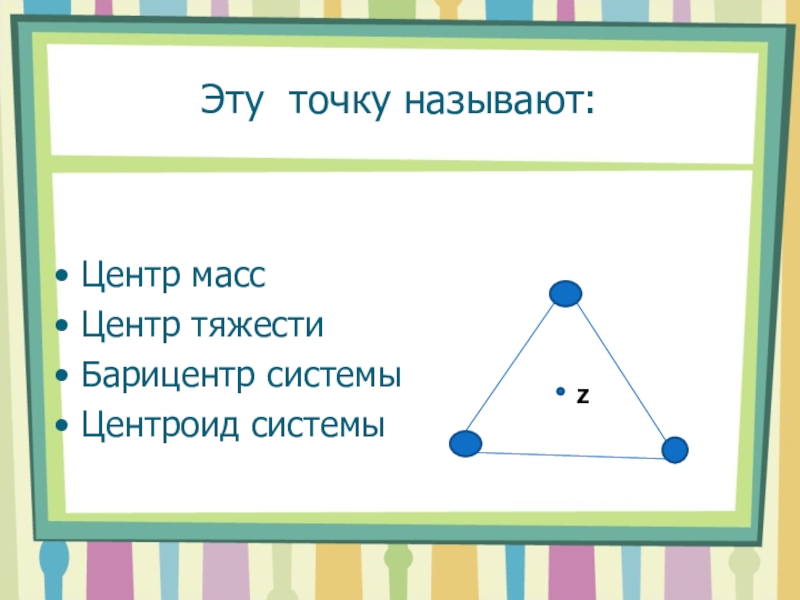
- 5. Эту точку называют:Центр массЦентр тяжестиБарицентр системыЦентроид системыZ
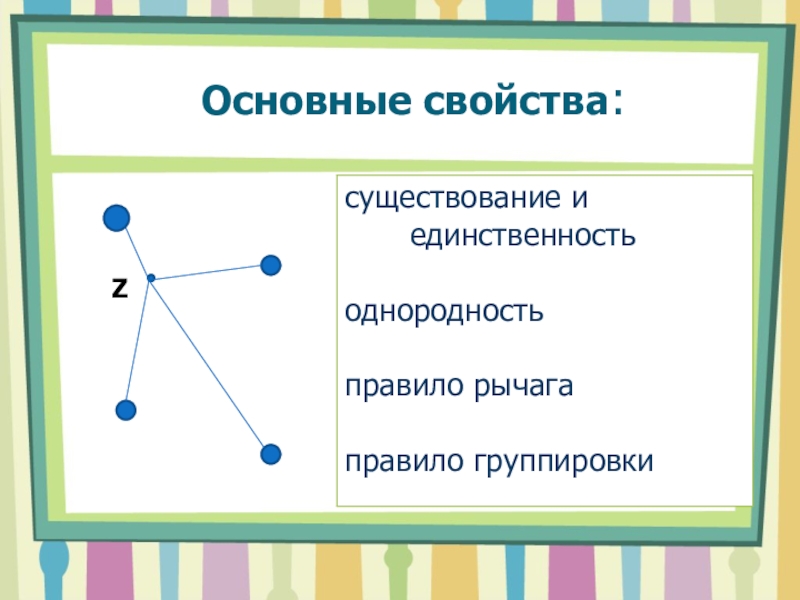
- 6. Основные свойства:Z
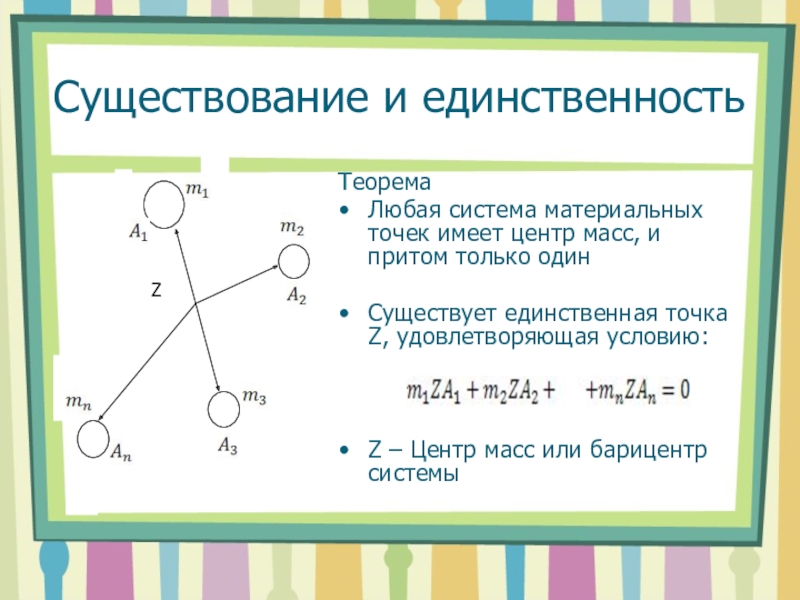
- 7. Существование и единственностьТеоремаЛюбая система материальных точек имеет
- 8. ОднородностьЕсли массу каждой точки системы умножить на
- 9. Правило рычага Если и - массы, расположенные
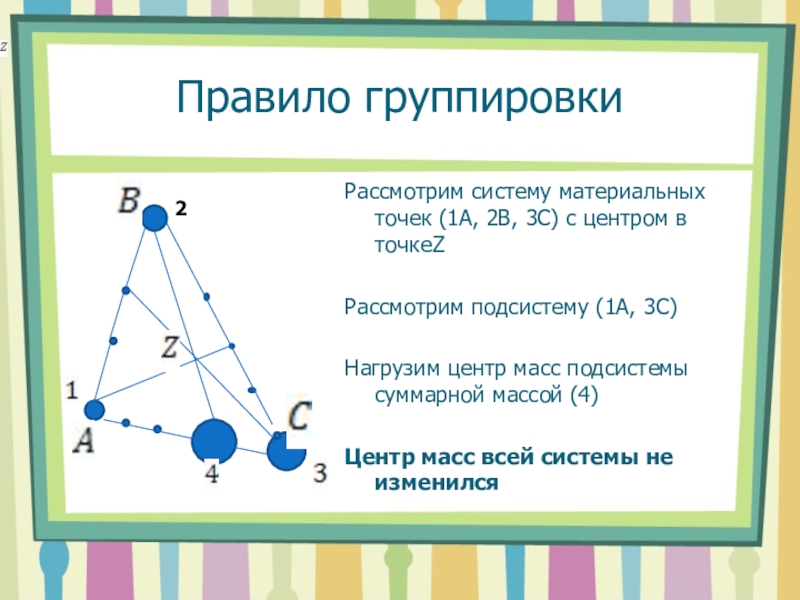
- 10. Правило группировкиРассмотрим систему материальных точек (1A, 2B,
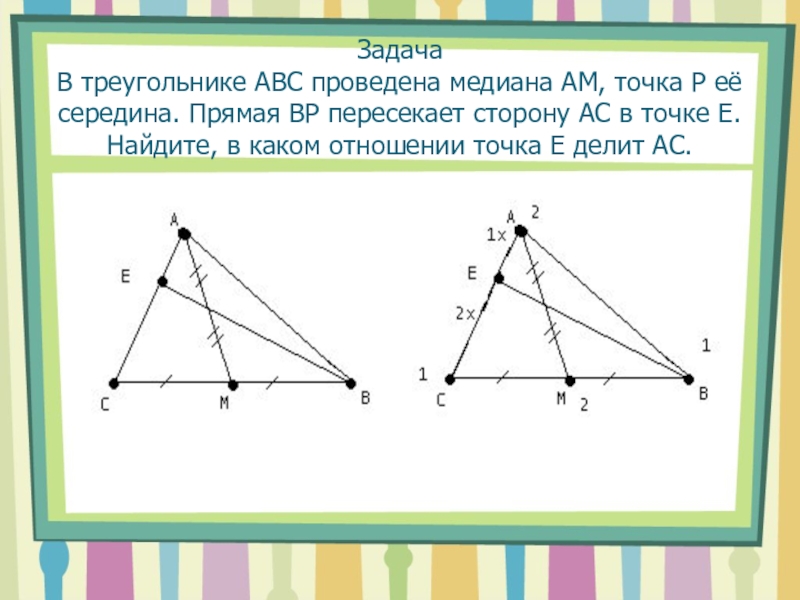
- 11. Задача В треугольнике АВС проведена медиана АМ,
- 12. Задача . На стороне АС треугольника АВС
- 13. Подборка задач из ОГЭ и ЕГЭ, решаемых
- 14. Скачать презентанцию
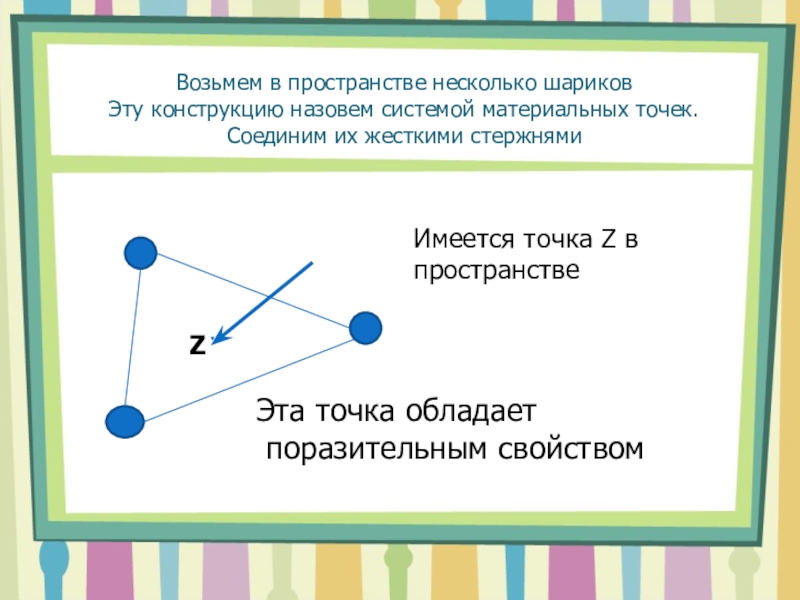
Возьмем в пространстве несколько шариков Эту конструкцию назовем системой материальных точек. Соединим их жесткими стержнямиZИмеется точка Z в пространствеЭта точка обладает поразительным свойством
Слайды и текст этой презентации
Слайд 1Барицентрический метод решения
геометрических задач
Выполнила: Машко Н.И.
учитель математики,
высшая квалификационная
категория
Слайд 2Возьмем в пространстве несколько шариков Эту конструкцию назовем системой материальных точек. Соединим
их жесткими стержнями
Z
Имеется точка Z в пространстве
Эта точка обладает
поразительным
свойствомСлайд 7Существование и единственность
Теорема
Любая система материальных точек имеет центр масс, и
притом только один
Существует единственная точка Z, удовлетворяющая условию:
Z – Центр
масс или барицентр системыСлайд 8Однородность
Если массу каждой точки системы умножить на одно и то
же положительное число , то центр масс не изменится
Слайд 9Правило рычага
Если и - массы, расположенные в точках
и и, то их барицентр Z
находится на отрезкеБарицентр Z делит отрезок обратно пропорционально массам
и
Z
Слайд 10Правило группировки
Рассмотрим систему материальных точек (1A, 2B, 3C) c центром
в точкеZ
Рассмотрим подсистему (1А, 3С)
Нагрузим центр масс подсистемы суммарной
массой (4)Центр масс всей системы не изменился
2
Слайд 11Задача В треугольнике АВС проведена медиана АМ, точка Р её середина.
Прямая ВР пересекает сторону АС в точке Е. Найдите, в
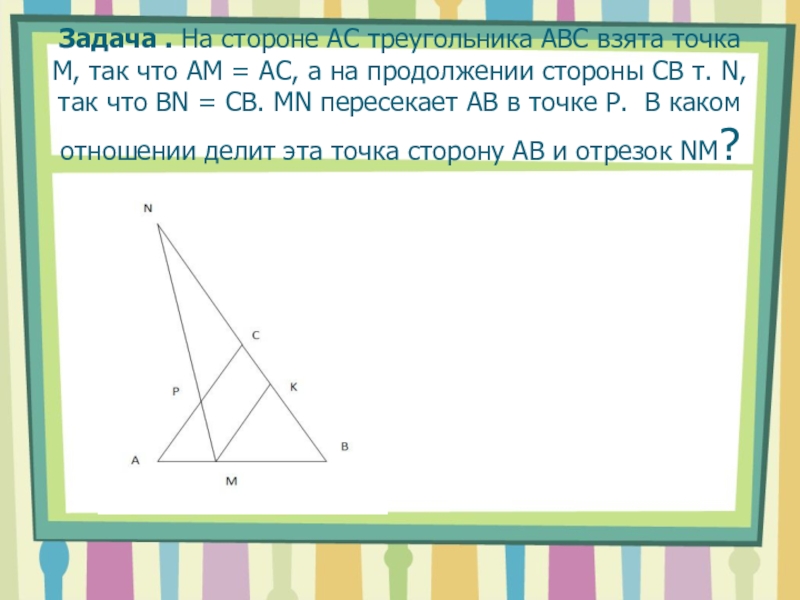
каком отношении точка Е делит АС.Слайд 12Задача . На стороне АС треугольника АВС взята точка М,
так что АМ = АС, а на продолжении стороны СВ
т. N, так что BN = CB. MN пересекает АВ в точке P. В каком отношении делит эта точка сторону АВ и отрезок NM?Слайд 13Подборка задач из ОГЭ и ЕГЭ, решаемых с помощью метода
масс
1.Площадь треугольника ABC равна 120, точка D лежит на отрезке
BC так, что BD:CD = 1: 2, биссектриса BK пересекает прямую AD в точке L. Найдите площадь четырехугольника KLDC, если AK:KC = 3:1.2.