C1 метод мажорант

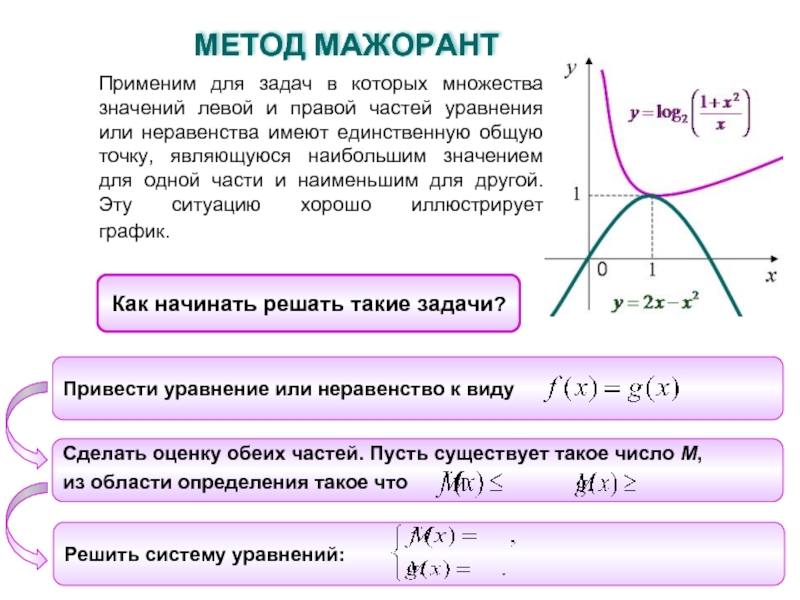
частей уравнения или неравенства имеют единственную общую точку, являющуюся наибольшим

Как начинать решать такие задачи?

МЕТОД МАЖОРАНТ

Привести уравнение или неравенство к виду

Сделать оценку обеих частей. Пусть существует такое число М,
из области определения такое что

х верны неравенства:
Следовательно, данное уравнение равносильно системе:

уравнение равносильно системе:
При х = 0 второе уравнение обращается в

Ответ: х = 0.

Графическая иллюстрация

для суммы двух взаимно
обратных чисел) выполнено
Поэтому уравнение имеет решения,

принимает значение от 0,5 до 2.

Решение. Оценим обе части уравнения.

Графическая иллюстрация

Решение. Оценим обе части уравнения.

одновременно равны 1.
Следовательно, данное уравнение равносильно системе уравнений
.
Решение.

получаем:
Следовательно, левая часть равна правой, лишь при условии:
Значит, данное

Решая систему уравнений, получаем корни:

.

Заметим, что перемножив

Ответ:

Решите уравнение
Решение. Для решения уравнения
оценим его части:

Поэтому равенство возможно только при условии

Сначала решим второе уравнение:

Корни этого уравнения

Итак, данное уравнение имеет единственный корень х = 0.

Ответ: 0.

При х = -1 имеем:

которых уравнение
имеет решения. Найдите эти решения.
При всех значениях

При всех значения х выражения

Поэтому

Следовательно, левая часть уравнения не меньше 4, а правая часть – не больше 4. Получаем систему:

Решение. Перепишем уравнение в виде