Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
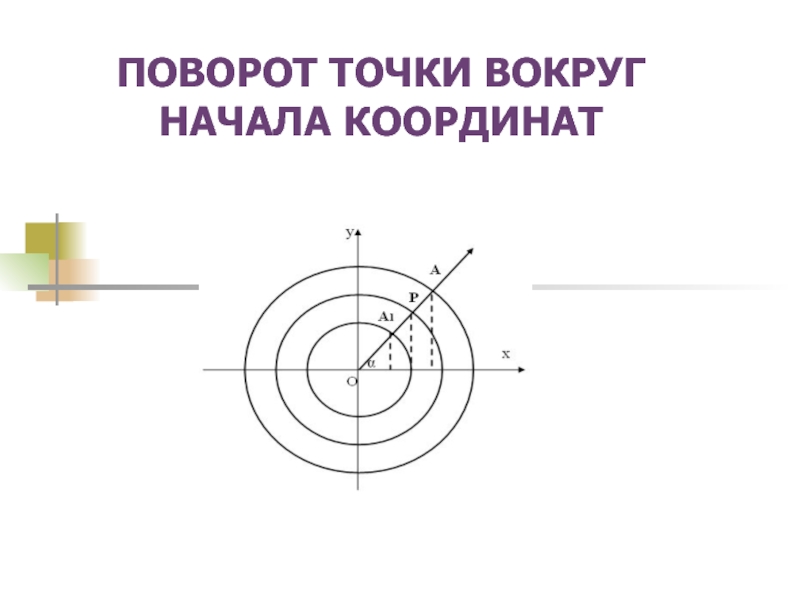
ПОВОРОТ ТОЧКИ ВОКРУГ НАЧАЛА КООРДИНАТ
Содержание
- 1. ПОВОРОТ ТОЧКИ ВОКРУГ НАЧАЛА КООРДИНАТ
- 2. Зачатки тригонометрических познаний зародились в древности
- 3. Николай КОПЕРНИК (1473
- 4. Иоганн КЕПЛЕР(1571 – 1630)Исаак НЬЮТОН(1643 – 1727)Готфрид ЛЕЙБНИЦ
- 5. ЗАДАНИЕ ПОВОРОТОВ Пусть луч, выходящий из точки
- 6. декартова система разбивается координатными осями на четыре
- 7. ПОВОРОТ ПОВОРОТ ТОЧКИ ВОКРУГ НАЧАЛА КООРДИНАТ
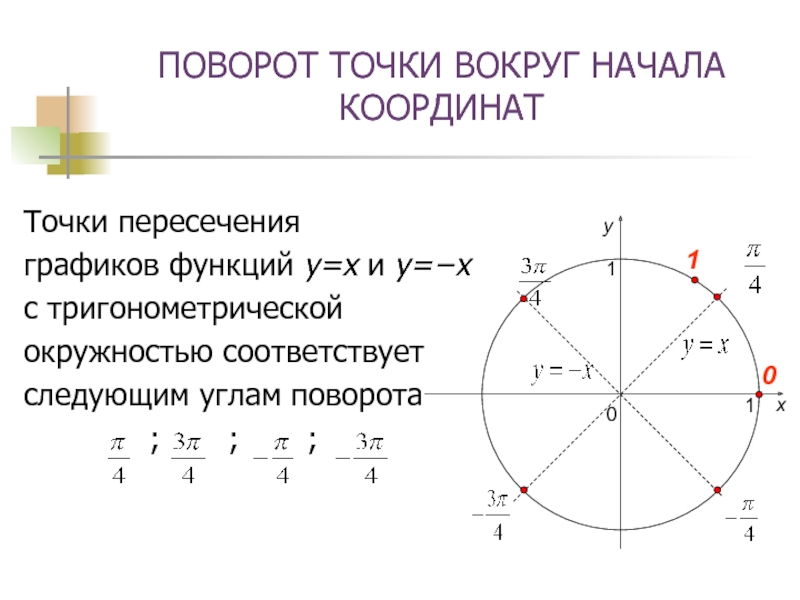
- 8. ПОВОРОТ ТОЧКИ ВОКРУГ НАЧАЛА КООРДИНАТТочки пересеченияграфиков функций
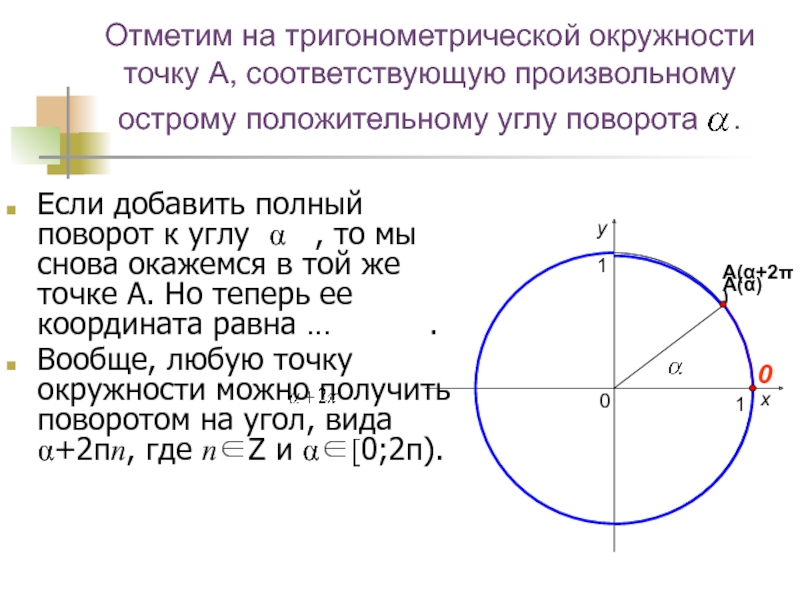
- 9. Отметим на тригонометрической окружности точку А, соответствующую
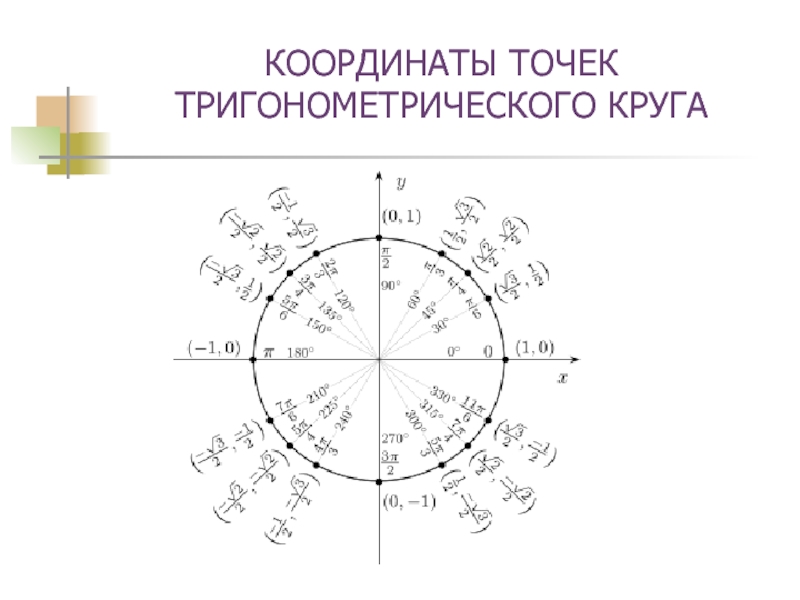
- 10. КООРДИНАТЫ ТОЧЕК ТРИГОНОМЕТРИЧЕСКОГО КРУГА
- 11. КООРДИНАТЫ ТОЧЕК ТРИГОНОМЕТРИЧЕСКОГО КРУГА
- 12. Скачать презентанцию
Зачатки тригонометрических познаний зародились в древности
Слайды и текст этой презентации
Слайд 4Иоганн КЕПЛЕР
(1571 – 1630)
Исаак НЬЮТОН
(1643 – 1727)
Готфрид ЛЕЙБНИЦ
(1646 – 1716)
С
факелом тригонометрии доказывали движение планет, пути комет и приливы океанов
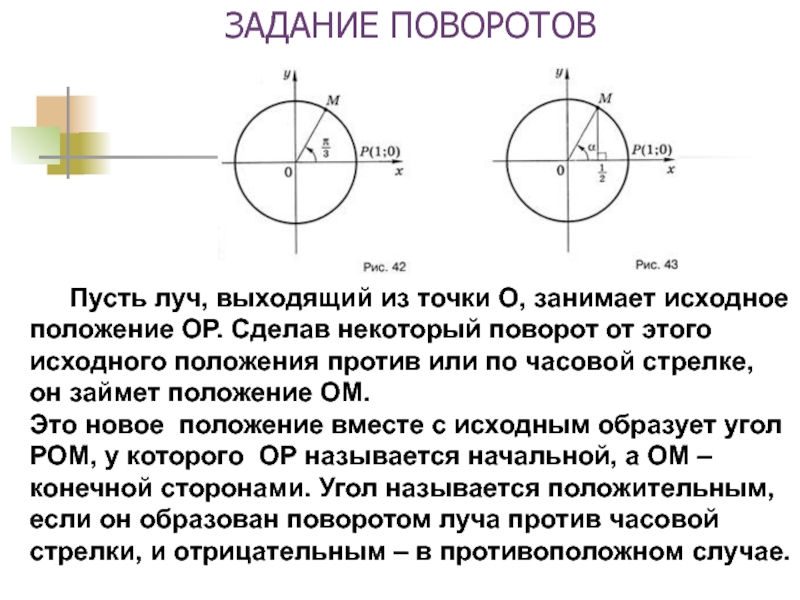
Слайд 5ЗАДАНИЕ ПОВОРОТОВ
Пусть луч, выходящий из точки О, занимает
исходное положение ОР. Сделав некоторый поворот от этого исходного положения
против или по часовой стрелке, он займет положение ОМ.Это новое положение вместе с исходным образует угол РОМ, у которого ОР называется начальной, а ОМ – конечной сторонами. Угол называется положительным, если он образован поворотом луча против часовой стрелки, и отрицательным – в противоположном случае.
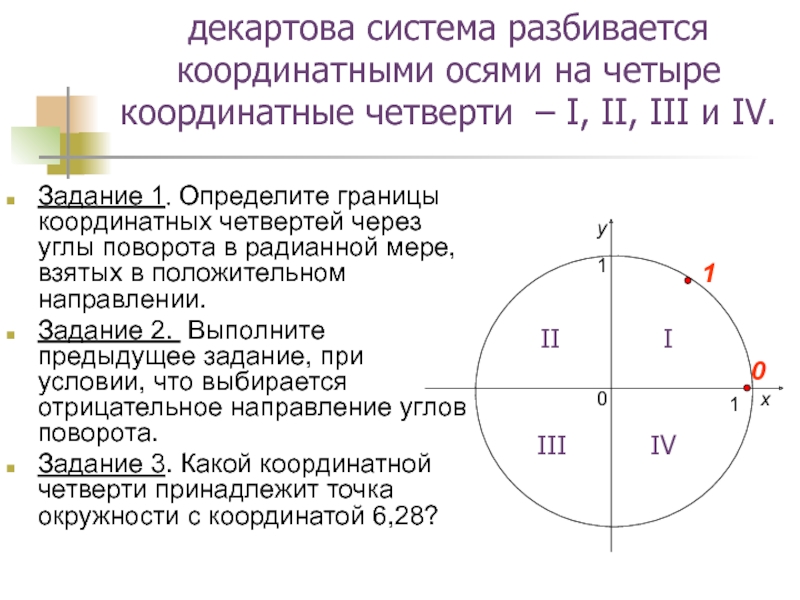
Слайд 6декартова система разбивается координатными осями на четыре координатные четверти –
I, II, III и IV.
Задание 1. Определите границы координатных четвертей
через углы поворота в радианной мере, взятых в положительном направлении. Задание 2. Выполните предыдущее задание, при условии, что выбирается отрицательное направление углов поворота.
Задание 3. Какой координатной четверти принадлежит точка окружности с координатой 6,28?
x
y
0
1
1
0
1
I
II
III
IV
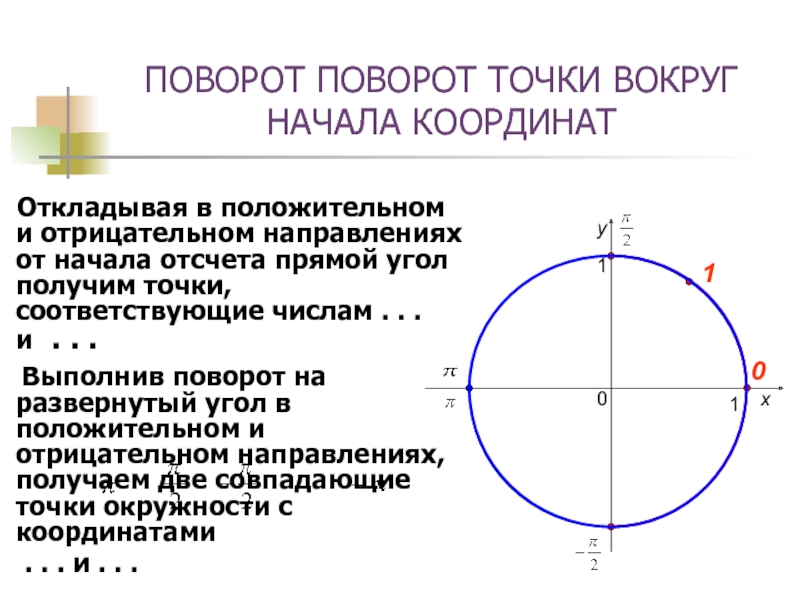
Слайд 7ПОВОРОТ ПОВОРОТ ТОЧКИ ВОКРУГ НАЧАЛА КООРДИНАТ
Откладывая в положительном
и отрицательном направлениях от начала отсчета прямой угол получим точки,
соответствующие числам . . . и . . .Выполнив поворот на развернутый угол в положительном и отрицательном направлениях, получаем две совпадающие точки окружности с координатами
. . . и . . .
.
x
y
0
1
1
0
1
Слайд 8ПОВОРОТ ТОЧКИ ВОКРУГ НАЧАЛА КООРДИНАТ
Точки пересечения
графиков функций y=x и y=x
с тригонометрической
окружностью соответствует
следующим углам поворота
; ; ;
x
y
0
1
1
0
1
Слайд 9Отметим на тригонометрической окружности точку А, соответствующую произвольному острому положительному
углу поворота .
Если добавить полный поворот к углу
α , то мы снова окажемся в той же точке А. Но теперь ее координата равна … .Вообще, любую точку окружности можно получить поворотом на угол, вида α+2n, где n и α[0;2).
x
y
0
1
1
0
A(α)
A(α+2)