Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Числовые неравенства и их свойства
Содержание
- 1. Числовые неравенства и их свойства
- 2. ОглавлениеПонятие числового неравенстваСвойство 1Свойство 2Свойство 3Свойство
- 3. Определение: 1.Действительное число а больше
- 4. > «больше»< «меньше»>=«больше или равно»
- 5. а>0 означает, что а – положительное число;а>=0 означает, что а –неотрицательное число (положительное или 0);а
- 6. Свойства числовых неравенств
- 7. Свойство1.Если a>b и b>c, то a>c.Доказательство.а>b а-b>0 b>c b-с>0 (а-b)+(b-с)>0 а-с>0 а>с Оглавление
- 8. Если к обеим частям неравенства прибавить одно
- 9. Свойство 3 Если а>b и m>0, то am>bm Если a>b и m4bЕсли a-9bЕсли a>b, то -a
- 10. Свойство 4 Если a>b и c>d, то a+c>b+dДоказательство. a>b (свойство 2)c>d(Свойство 2)a+c>b+cc+b>d+ba+c>b+d (Свойство 1) Оглавление
- 11. Свойство 5 Если a,b,c,d – положительные числа
- 12. Свойство 6 Если a и b -
- 13. Свойство 7 Если а и b
- 14. Применение свойств числовых неравенств
- 15. Дано:8 < a < 10
- 16. Дано: 5
- 17. Доказательство :Докажите,что функция y=-5x+4 убывает Если х
- 18. Доказательство : Если х > xДокажите, что
- 19. Найдите область значений функции: 1)
- 20. Скачать презентанцию
ОглавлениеПонятие числового неравенстваСвойство 1Свойство 2Свойство 3Свойство 4Свойство 5Свойство 6Свойство 7Применение свойств:8 класс9 класс10 – 11 классы
Слайды и текст этой презентации
Слайд 2Оглавление
Понятие числового
неравенства
Свойство 1
Свойство 2
Свойство 3
Свойство 4
Свойство 5
Свойство 6
Свойство
7
Слайд 3Определение: 1.Действительное число а больше действительного числа b, если их
разность
а-b – положительное число.
2. Действительное число а меньше
действительного числа b, если их разность а-b – отрицательное число.Пишут a>b или a
Слайд 5а>0 означает, что а – положительное число;
а>=0 означает, что а
–неотрицательное число (положительное или 0);
а
число.
а<=0 означает, что а – неположительное число (отрицательное или 0).
Оглавление
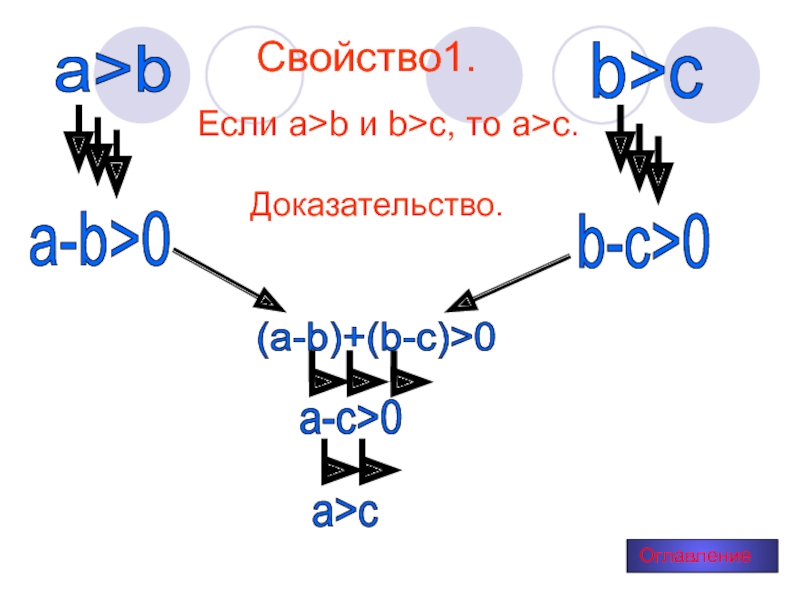
Слайд 7Свойство1.
Если a>b и b>c, то a>c.
Доказательство.
а>b
а-b>0
b>c
b-с>0
(а-b)+(b-с)>0
а-с>0
а>с
Оглавление
Слайд 8Если к обеим частям неравенства прибавить одно и тоже число,
то знак неравенства следует сохранить
Если a>b, то a+c>b+c.
Примеры:
Если a
a+7Если a>b, то a-5>b-5
Свойство 2
Оглавление
Слайд 9Свойство 3
Если а>b и m>0, то am>bm
Если a>b
и m
на одно и то жеположительное число, то знак
неравенства следует сохранить.
Если обе части неравенства
умножить на одно и то же
отрицательное число, то знак
неравенства следует изменить.
Примеры:
Если a>b, то 4a>4b
Если a Если a>b, то -a<-b Оглавление
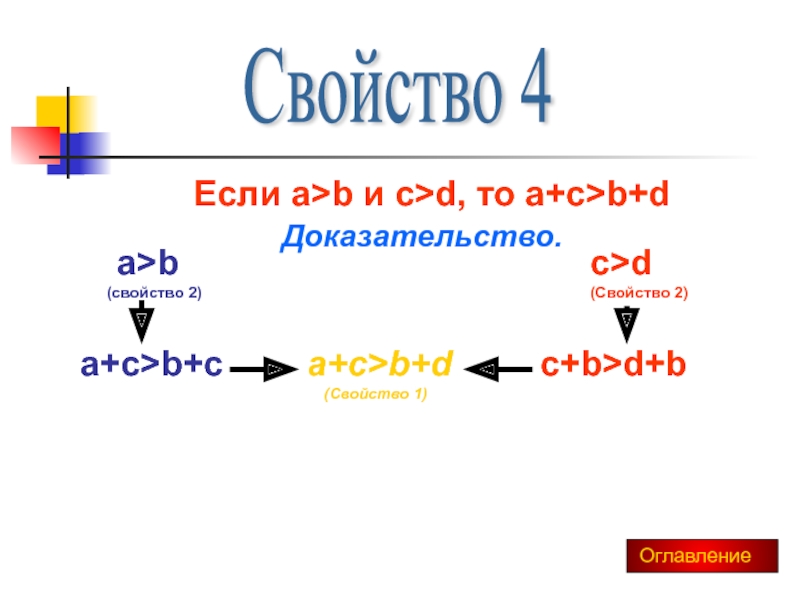
Слайд 10Свойство 4
Если a>b и c>d, то a+c>b+d
Доказательство.
a>b
(свойство
2)
c>d
(Свойство 2)
a+c>b+c
c+b>d+b
a+c>b+d
(Свойство 1)
Оглавление
Слайд 11Свойство 5
Если a,b,c,d – положительные числа и a>b, c>d,
ас >bd
Доказательство
a>b и c>0
(свойство 3)
ac>bc
c>d и b>0
(свойство 3)cb>db
ac>bd
(Свойство 1)
Оглавление
Слайд 12Свойство 6
Если a и b - неотрицательные числа и
a>b,
то a*n>b*n, где n - любое натуральное число.
Дополнение:
Если
n – нечетное число, то для любых чисел a и b из неравенства a>b следует неравенство
того же смысла a*n>b*n.
Оглавление
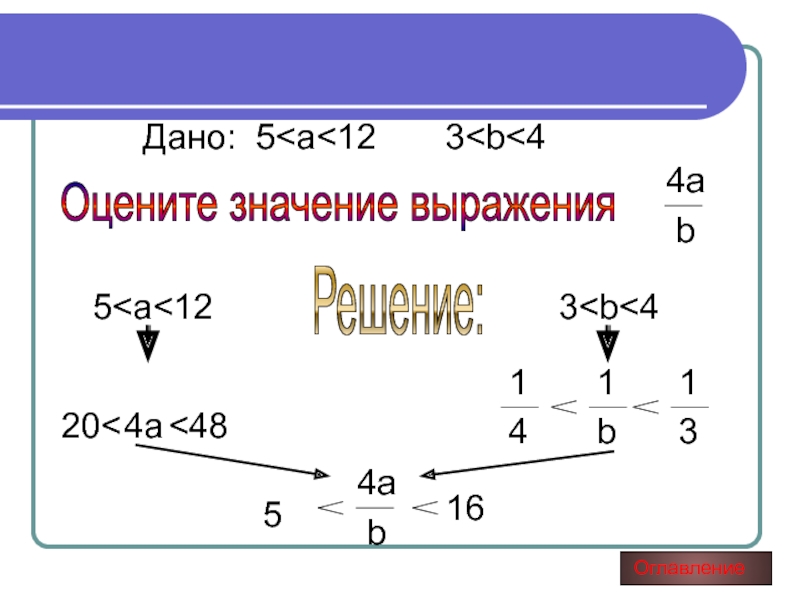
Слайд 15Дано:
8 < a < 10
1 < b
2Оцените значение выражения 2а-3b
Решение:
2а
8<а<10
<20
16<
1 <-3 -3b -6< 10<2а-3b<17 8 класс
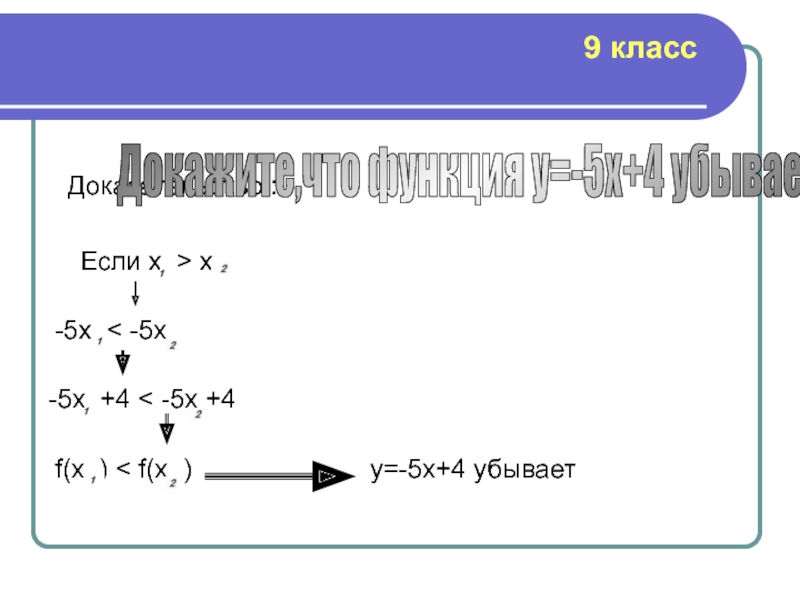
Слайд 17Доказательство :
Докажите,что функция y=-5x+4 убывает
Если х > x
-5x
-5x
-5x +4 < -5x +4
f(x ) < f(x )
y=-5x+4 убывает
9
класс
Слайд 18Доказательство :
Если х > x
Докажите, что функция y=x+3x возрастает
х > x
3х > 3x
Х + 3X >X + 3X
f(x
)>f(x )y= x + 3x возрастает
Оглавление
Слайд 19Найдите область значений функции:
1) y =
2,5cosx – 1,5
7) y = cos²(x + π/4) + sin2x2) y = –(sin5x)/5 8) y = –6/π arctgx + 2
3) у = 3 – 2sinx 9) y = 2/π arcsinx + 3
4) y = 2sin²x – 5 10) y = 4π – 2arccosx
5) y = 2 – cos²x 11) y = 3arcsinx + π/2
6) y = 4cos²3x – 2 12) y = 2arcsinx + 3arccosx
Найдите область определения функции:
1) y = arcsin4x 4) y = arccos(–3x)
2) y = arcsin(5 – 2x) 5) y = arccos(5x–4)
3) y = arcsin(x² – 3) 6) y = arccos(8 – x²)
Имеет ли смысл выражение:
__ __
1) arcsin(4 – √20) 2) arccos(7 – √30)?
Примените свойства числовых неравенств
