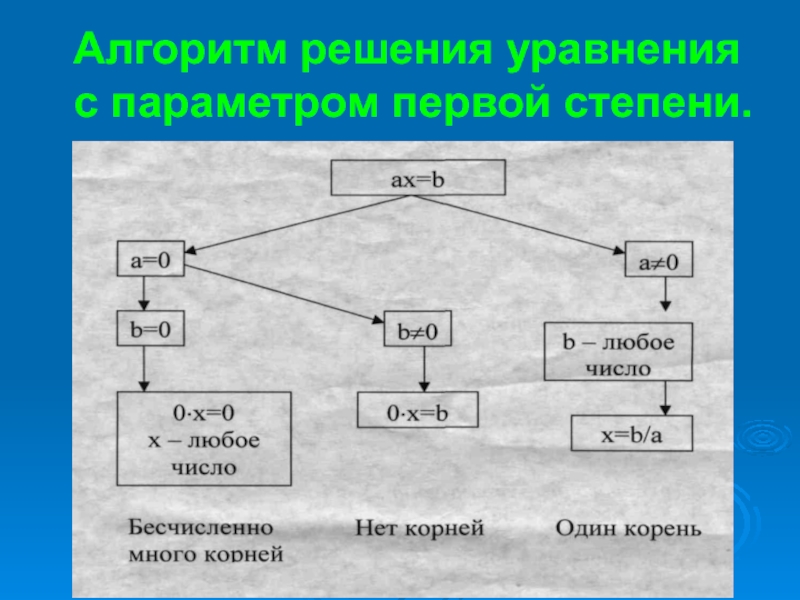
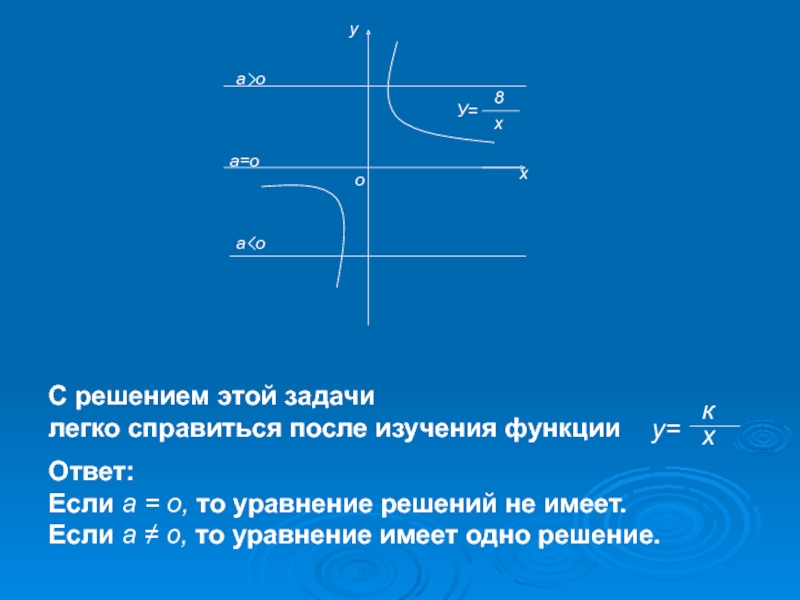
Задачи с параметрами

задачи с параметрами.

Трудность их решения состоит в:
выборе способа решения,

отслеживании возникающих ветвлений,
исследовании всех вариантов решения.

Задачи с параметрами - незаменимое средство для тренировки логического мышления.

Особенность работы – ориентированность её на возможность самостоятельного овладения учащимися содержанием.

параметрами для подготовки к ГИА.
Задачи работы:
Изучить алгоритм решения некоторых

задач с параметрами.
Научиться выбирать способ решения задач с параметрами.
Развивать свои навыки исследовательской и познавательной деятельности.

считается заданным фиксированным или произвольным действительным числом, или числом, принадлежащим

заранее оговоренному множеству.

Если в уравнении некоторые коэффициенты заданы не конкретными числовыми значениями, а обозначены буквами, то они называются параметрами, а уравнение параметрическим.

решения.

Для каждой допустимой системы значений параметров найти соответствующее множество

решений.

решений в зависимости от значения параметра
требуется найти все те

значения параметра, при которых указанные уравнения, неравенства, их системы и совокупности имеют заданное число решений
Уравнения, неравенства, их системы и совокупности, для которых при искомых значениях параметра множество решений удовлетворяет заданным условиям в области определения.

уравнение ах=1.
Решение.
если а = 0 - то нет решения
если

а = 0 - то х = .
Ответ: если а = 0 - то х = ; если а = 0 то нет решения

1

а

а

1

уравнения ах=8.
Рассмотрим уравнение:
х
8
а=
у = а - семейство горизонтальных прямых;

8
х
у=
- графиком

является гипербола.

Если а = о, то уравнение решений не имеет.


Если а ≠ о, то уравнение имеет одно решение.

функции
к
х
у=
Ответ:
Если а = о, то уравнение решений не имеет.
Если

а ≠ о, то уравнение имеет одно решение.

решение неравенства ax +1 >0.
Решение: если а=0,то 0х +1>0, 0x>-1

при любом х. если а>0, то х>- если a<0, то х<-
Ответ: при а=0 , х любое ; при а>0, х>- ; при a<0, то х<-

1

1

1

1

а

а

а

а

х. Для каждого значения р определить координаты точки касания.
Решение: Парабола

у=-2х +рх-50 касается оси х значит квадратный трехчлен
-2х +рх-50 имеет единственный корень. Следовательно дискриминант этого квадратного трехчлена равен 0: D=p -400, p -400=0, p= ±20.

Решение квадратных уравнений по текстам ГИА.

2

2

2

2

2

у=-2(х+5) , х=-5 – абсцисса точки касания

параболы с осью х, (-5;0) – координаты точки касания.
При p= 20, у=-2х +20х-50, у=-2(х-5) , х=5 – абсцисса точки касания параболы с осью х, (5;0) – координаты точки касания.

Ответ: при p= -20, координаты точки касания – (-5;0); при p= 20 - (5;0).

2

2

2

2

пересекает ровно в двух различных точках график функции, заданной условиями:

3х + 5, если х < -2,
у= -х + 2, если -2 < х ≤ 2,
х - 2, если х > 2.

Решение:
Построим график
данной функции.

х

0

2

-2

2

-1

А

у

(-2; -1)
-1 = -2k;

k = 0,5
у = 0; k = 0.
Значит, 0 < k ≤ 0,5.

2). У = х – 2; k = 1.
у = 3х +5; k = 3.
Значит, 1 ≤ k < 3.

Ответ: (0; 0,5] U [1; 3).

у

х

0

2

-2

2

-1

А

у

параметрические уравнения и неравенства,
что значит решить задачу с параметрами,

изучен алгоритм решения наиболее распространенных задач с параметрами,
познакомилась с четырьмя основными типами задач с параметрами,
Научилась решать уравнения и неравенства с параметрами различными методами.

с параметрами. М., Математика в школе №6/99 с.60-68
2. Звавич Л.И.

и др. Алгебра и начала анализа. 3600 задач для школьников и поступающих в вузы.- М.: Дрофа. 1999 г. – 382 с.
3. Кожухов С.К. Об одном классе параметрических задач. – М., Математика в школе, №3/96 с.45-49
4. Кожухов С.К Различные способы решений задач с параметрами. – М., Математика в школе, №6/98 с.9-12
5. Крамар В.С. Примеры с параметрами и их решения. Пособие для поступающих в вузы. – М.:АРКТИ 200 – 48 с.