Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Движения в пространстве Центральная симметрия
Содержание
- 1. Движения в пространстве Центральная симметрия
- 2. Форма урока: Урок – семинар, решение проблемного
- 3. Симметрия является той идеей, посредством которой человек
- 4. Движение пространства - это отображение пространства на себя, сохраняющее расстояние между точками.
- 5. Центральная симметрия
- 6. Центральная симметрия – отображение пространства на себе,
- 7. Слайд 7
- 8. Слайд 8
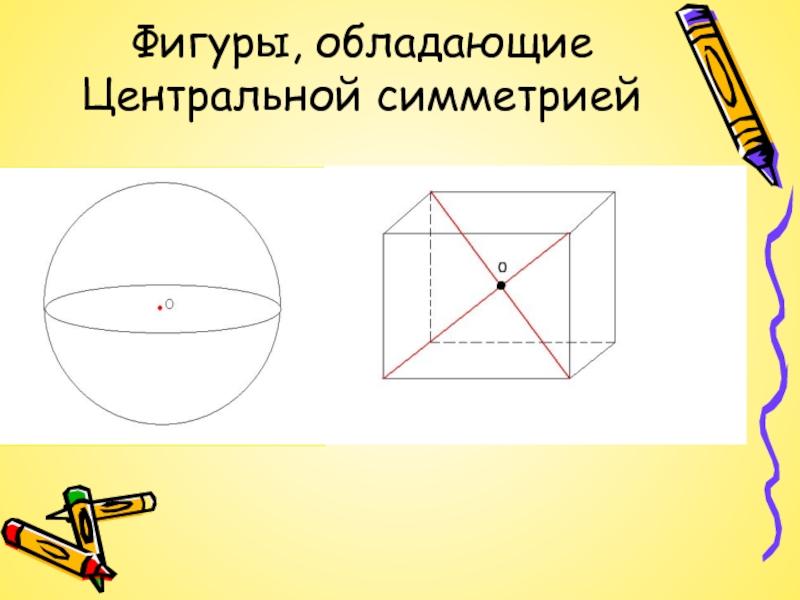
- 9. Фигуры, обладающие Центральной симметрией
- 10. Ст. метро Сокол
- 11. Ст. метро Римская
- 12. Павильон Культура, ВВЦ
- 13. .О
- 14. Осевая симметрия
- 15. Осевой симметрией с осью а называется такое
- 16. Х y Z О M(x;y;z)M1 (x1 ;y1;z1)Докажем,
- 17. ДоказательствоРассмотрим теперь любые две точки A(x1; y1;
- 18. ПрименениеОсевая симметрия встречается очень часто. Ее можно
- 19. Слайд 19
- 20. Применение осевой симметрии в жизниАрхитектурные строения
- 21. Снежинки и тело человека
- 22. Эйфелева Башнясова
- 23. Что может быть больше похоже на мою
- 24. Отображение объемной фигуры, при котором каждой ее
- 25. Теорема 1. Отражение в плоскости сохраняет расстояния
- 26. Докажем, что зеркальная симметрия – это движение
- 27. Если точка М не лежит в плоскости
- 28. Симметрия относительно плоскости (зеркальная симметрия) пространства есть
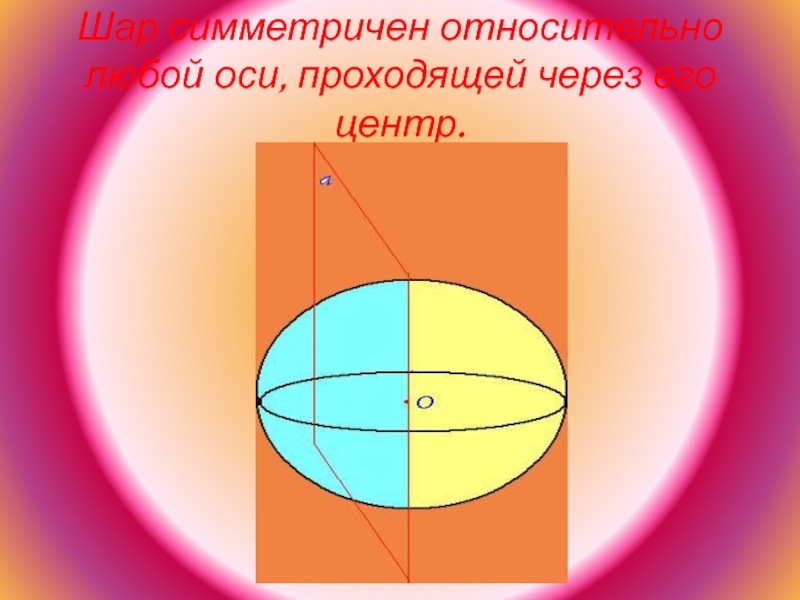
- 29. Шар симметричен относительно любой оси, проходящей через его центр.
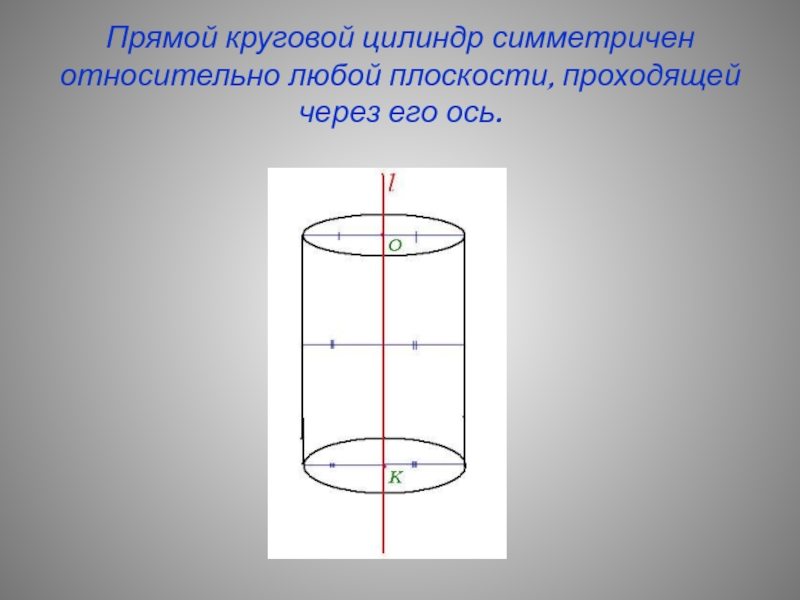
- 30. Прямой круговой цилиндр симметричен относительно любой плоскости, проходящей через его ось.
- 31. Правильная n-угольная пирамида при четном n
- 32. Обычно считают ,что наблюдаемый в зеркале двойник
- 33. Предположим ,что одна половина объекта является зеркальным
- 34. Здание ЕНУ им. Л.Н Гумилева
- 35. Параллельный перенос
- 36. Движение плоскостиДвижение
- 37. Слайд 37
- 38. ПрименениеМы так же можем увидеть «параллельный перенос
- 39. Слайд 39
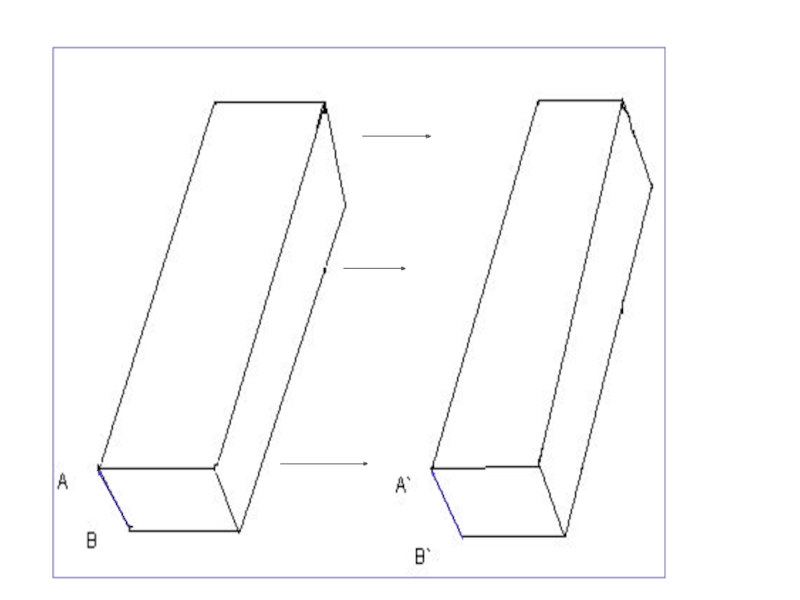
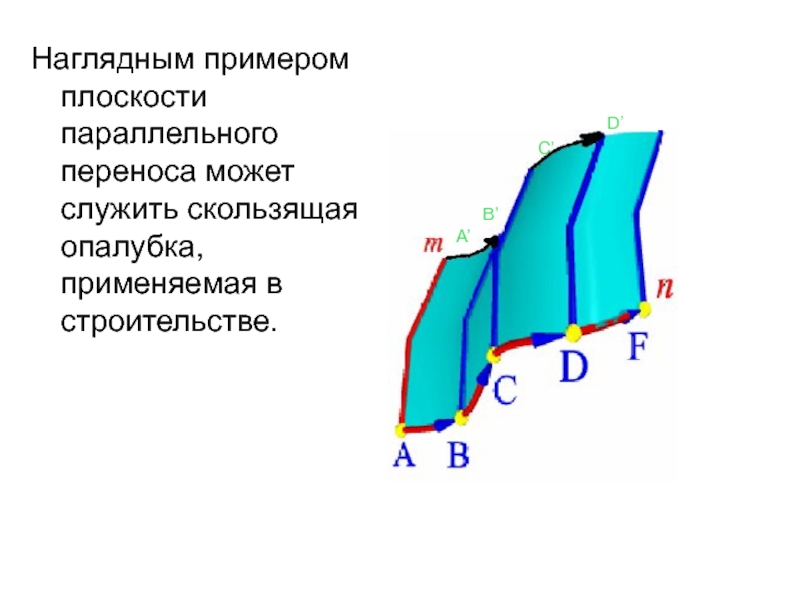
- 40. Наглядным примером плоскости параллельного переноса может служить скользящая опалубка, применяемая в строительстве. A’B’C’D’
- 41. Слайд 41
- 42. Слайд 42
- 43. Слайд 43
- 44. Слайд 44
- 45. Слайд 45
- 46. Спасибо за урок
- 47. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Урок геометрии в
11 классе
учителя Текутовой И.Н.
Движения в пространстве
Центральная симметрия
Слайд 2Форма урока:
Урок – семинар, решение проблемного вопроса
Цели урока:
Актуализировать личностное осмысление
учащимися учебного материала «Движения в пространстве»
Содействовать сознательному пониманию прикладного значения
темы, развитию умения видеть в окружающей действительности изучаемые виды движенийРазвивать познавательный интерес к построению образов объектов при различных видах движений
Способствовать грамотному усвоению темы, отработке практических навыков
Слайд 3Симметрия является той идеей, посредством которой человек на протяжении веков
пытался постичь и создать порядок, красоту и совершенство.
Г. Вейль.
Слайд 4Движение пространства - это отображение пространства на себя, сохраняющее расстояние
между точками.
Слайд 6Центральная симметрия – отображение пространства на себе, при котором любая
точка М переходит в симметричную ей точку М1 относительно данного
центра О.Слайд 15Осевой симметрией с осью а называется такое отображение пространства на
себя, при котором любая точка М переходит в симметричную ей
точку М1 относительно оси а.Осевая симметрия – это движение.
а
Осевая симметрия
M
M1
Слайд 16
Х
y
Z
О
M(x;y;z)
M1 (x1 ;y1;z1)
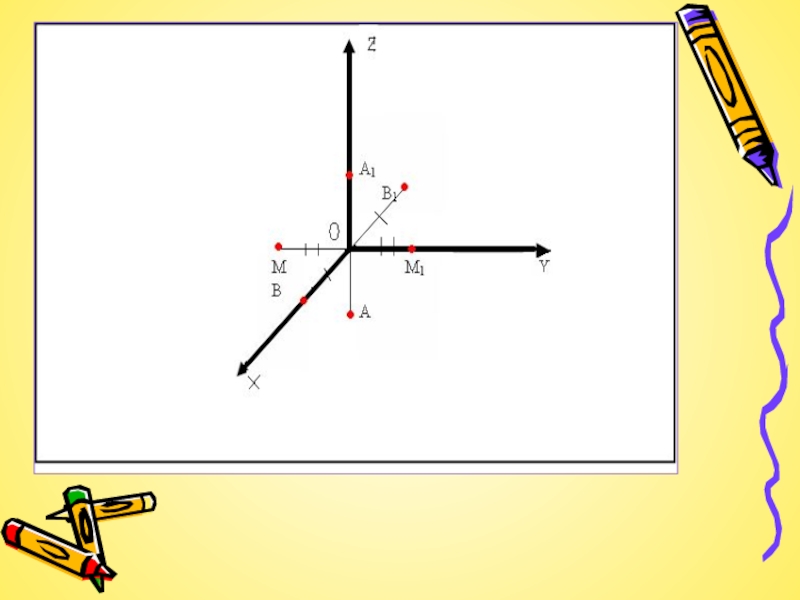
Докажем, что осевая симметрия
является движением. Для этого введем прямоугольную систему координат Oxyz так,
чтобы ось Oz совпала с осью симметрии, и установим связь между координатами двух точек M(x;y;z) и M1(x1;y1 ;z1) симметричных относительно оси Oz. Если точка М не лежит на оси Oz, то ось Oz:1) проходит через середину отрезка MM1 и 2) перпендикулярна к нему. Из первого условия по формулам для координат середины отрезка получаем (x+x1)/2=0 и (y+y1)/2=0, откуда x1=-x и y1=-z. Второе условие означает, что аппликаты точек M и M1 равны: z1=z.
Доказательство
Слайд 17Доказательство
Рассмотрим теперь любые две точки A(x1; y1; z1) и B(x2;y2;z2)
и докажем, что расстояние между симметричными им точками A1 и
B1 равно AB. Точки A1 и B1 имеют координаты A1(-x1;-y1;-z1) и B1(-x1;-y1;-z1) По формуле расстояния между двумя точками находим: AB=\/(x2-x1)²+(y2-y1)²+(z2-z1),A1B1=\/(-x2+x1)²+(-y2+y1)²+(-z2+z1). Из этих соотношений ясно, что AB=A1B1, что и требовалось доказать.
Слайд 18Применение
Осевая симметрия встречается очень часто. Ее можно увидеть как в
природе: листья растений или цветы, тело животных насекомых и даже
человека, так и в творении самого человека: здания, автомобили, техника и многое другое.Слайд 23Что может быть больше похоже на мою руку или мое
ухо , чем их собственное отражение в зеркале ? И
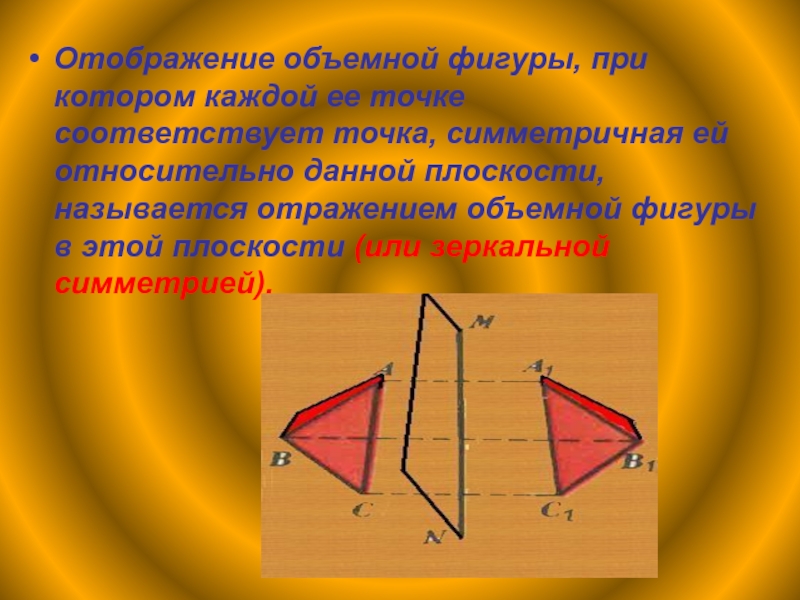
все же руку которую я вижу в зеркале , нельзя поставить на место настоящей руки. Эммануил Кант . Зеркальная симметрияСлайд 24Отображение объемной фигуры, при котором каждой ее точке соответствует точка, симметричная
ей относительно данной плоскости, называется отражением объемной фигуры в этой плоскости
(или зеркальной симметрией).Слайд 25Теорема 1. Отражение в плоскости сохраняет расстояния и, стало быть, является
движением. Теорема 2. Движение, при котором все точки некоторой плоскости неподвижны, является
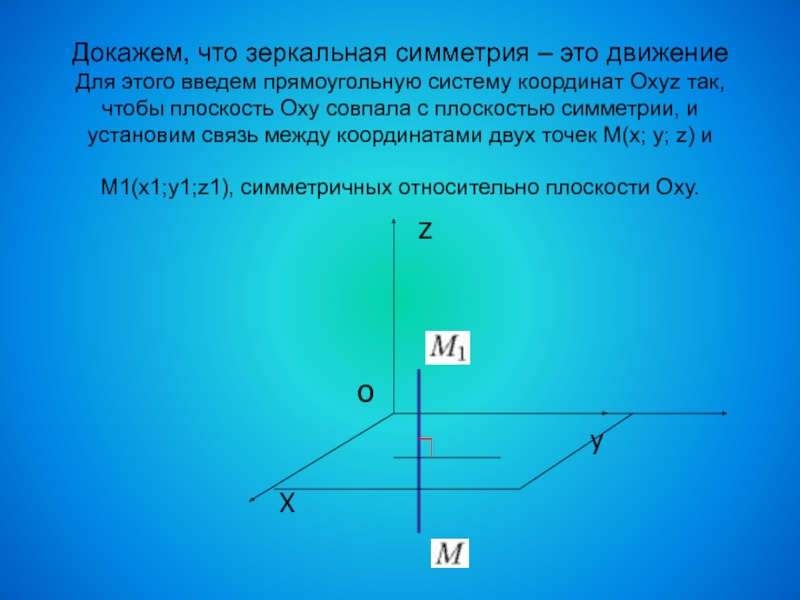
отражением в этой плоскости или тождественным отображением. Зеркальная симметрия задается указанием одной пары соответствующих точек, не лежащих в плоскости симметрии: плоскость симметрии проходит через середину отрезка, соединяющего эти точки, перпендикулярно к нему.Слайд 26Докажем, что зеркальная симметрия – это движение Для этого введем прямоугольную
систему координат Оxyz так, чтобы плоскость Оxy совпала с плоскостью
симметрии, и установим связь между координатами двух точек М(x; y; z) и М1(x1;y1;z1), симметричных относительно плоскости Оxy.y
X
z
о
Слайд 27Если точка М не лежит в плоскости Оxy, то эта
плоскость: 1) проходит через середину отрезка ММ1 и 2) перпендикулярна
к нему. Из первого условия по формуле координат середины отрезка получаем (z+z1)/2=0, откуда z1=-z. Второе условие означает, что отрезок ММ1 параллелен оси Оz, и. следовательно, х1=х, у1=у. М лежит в плоскости Oxy. Рассмотрим теперь две точки А (х1;у1;z1) и В (х2;у2;z2) и докажем, что расстояние между симметричными им точками А1(х1;у1;-z1) и В (х2;у2;-z2). По формуле расстояния между двумя точками находим: АВ= корень квадратный из (х2-х1)2+(у2-у1)2+(z2-z1)2, А1В1=корень квадратный из (х2-х1)2+(у2-у1)2+(-z2-z1)2. Из этих соотношений ясно, что и требовалось доказать.Слайд 28Симметрия относительно плоскости (зеркальная симметрия) пространства есть движение, а значит,
обладает всеми свойствами движений: переводит прямую в прямую, плоскость ---
в плоскость.Кроме того, это преобразование пространства, совпадающее со своим обратным: композиция двух симметрий относительно одной и той же плоскости есть тождественное преобразование.
При симметрии относительно плоскости все точки этой плоскости, и только они, остаются на месте (неподвижные точки преобразования). Прямые, лежащие в плоскости симметрии и перпендикулярные ей, переходят в себя. Плоскости, перпендикулярные плоскости симметрии также переходят в себя.
Симметрия относительно плоскости является движением второго рода (меняет ориентацию тетраэдра).
Слайд 31Правильная n-угольная пирамида при четном n симметрична относительно любой
плоскости, проходящей через ее высоту и наибольшую диагональ основания.
Слайд 32Обычно считают ,что наблюдаемый в зеркале двойник является точной копией
самого объекта. В действительности это не совсем так . Зеркало
не просто копирует объект , а меняет местами (переставляет) передние и задние по отношению к зеркалу части объекта . В сравнении с самим объектом его зеркальный двойник оказывается "вывернутым" вдоль направления перпендикулярного к плоскости зеркала .Этот эффект хорошо виден на одном рисунке и фактически незаметен на другом .Слайд 33Предположим ,что одна половина объекта является зеркальным двойником по отношению
к другой его половине . Такой объект называют зеркально симметричным
.Он преобразуется сам в себя при отражении в соответствующей зеркальной плоскости . Эту плоскость называют плоскостью симметрии .Слайд 36 Движение плоскости
Движение плоскости – это
взаимно однозначное преобразование точек плоскости при котором сохраняются расстояния: если
точка А переходит в А`, В – В`, то А`В`=АВПри движении так же сохраняются углы
Параллельный перенос – это отображение пространства на себя, при котором любая точка М переходит в точку М’, что MM’ = р
p
M
M’
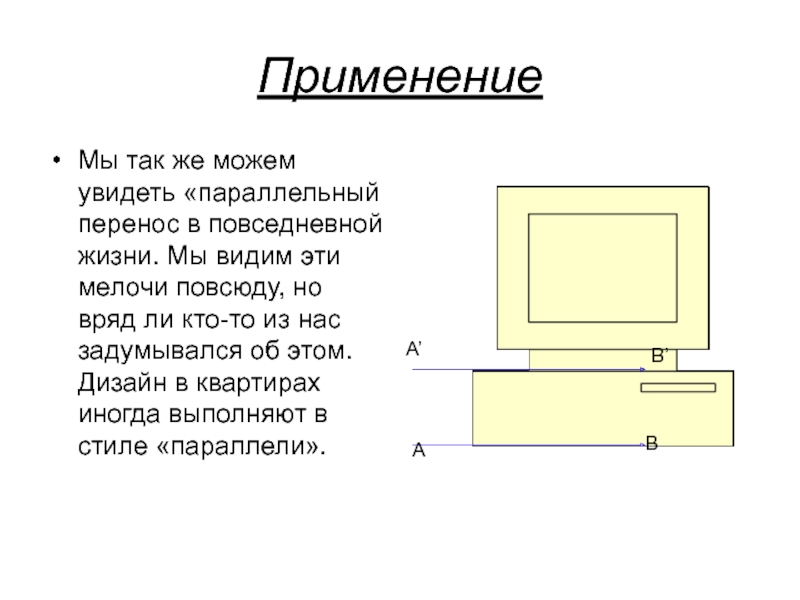
Слайд 38Применение
Мы так же можем увидеть «параллельный перенос в повседневной жизни.
Мы видим эти мелочи повсюду, но вряд ли кто-то из
нас задумывался об этом. Дизайн в квартирах иногда выполняют в стиле «параллели».А
В
А’
В’