Слайд 1ЕГЭ ПО МАТЕМАТИКЕ
2012
Лосева
Екатерина Анатольевна
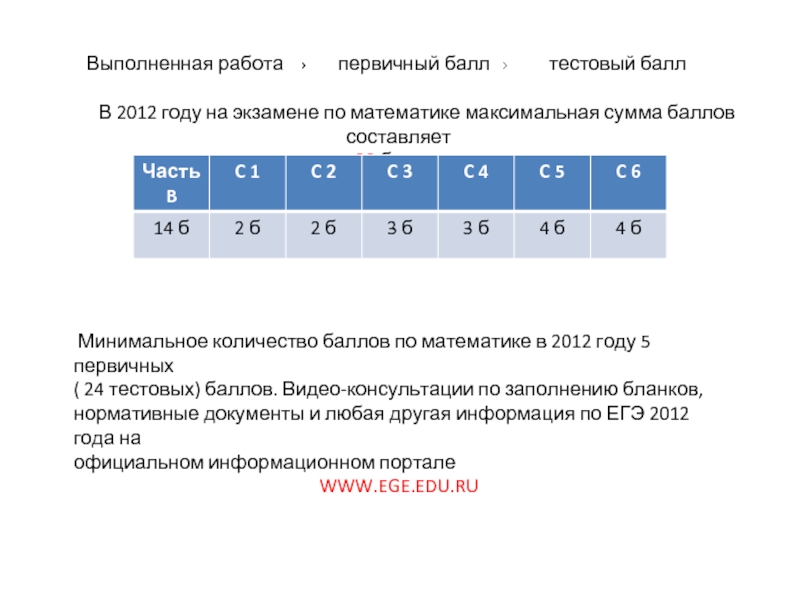
Слайд 2 Выполненная работа
первичный балл
тестовый балл
В 2012 году на экзамене по математике максимальная сумма баллов составляет
32 балла.
Минимальное количество баллов по математике в 2012 году 5 первичных
( 24 тестовых) баллов. Видео-консультации по заполнению бланков,
нормативные документы и любая другая информация по ЕГЭ 2012 года на
официальном информационном портале
WWW.EGE.EDU.RU
Слайд 3Сайты в помощь выпускникам
www.mathege.ru – открытый банк заданий части B.
Содержит десятки тысяч заданий первой части. Также позволяет пройти он-лайн
тестирование.
WWW.reshuege.ru - авторский сайт Гущина Д.Д.Позволяет самостоятельно генерировать варианты, тематические работы «Изюминка» сайта : доступны краткие решения практически всего открытого банка заданий.
www.alexlarin.net – на сайте размещены практически все тренировочные работы последних лет с ответами и комментариями.
Слайд 4B 1. Билет на автобус стоит 15 рублей. Какое максимальное
число билетов можно будет купить на 100 рублей после повышения
цены билета на 20 %?
Решение: После повышения цены билет будет стоить
Разделим 100 на 18 и возьмем в ответ целую часть результата деления:
Значит, можно купить 5 билетов.
Ответ:
В2. Шоколадка стоит 35 рублей. В воскресенье в супермаркете действует специальное предложение: заплатив за две шоколадки , покупатель получает три (одну в подарок). Сколько шоколадок можно получить на 200 рублей в воскресенье?
Решение:
,значит на 200 рублей можно купить две пары шоколадок и еще одну. Поучается в подарок 2 шоколадки. Всего 7 шоколадок.
Ответ:
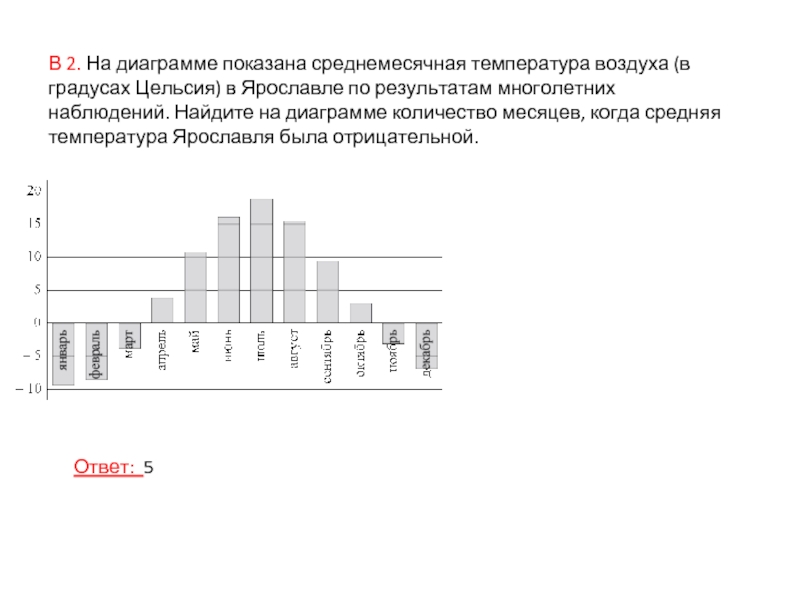
Слайд 5В 2. На диаграмме показана среднемесячная температура воздуха (в градусах
Цельсия) в Ярославле по результатам многолетних наблюдений. Найдите на диаграмме
количество месяцев, когда средняя температура Ярославля была отрицательной.
Ответ: 5
Слайд 6В 3. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с
размером клетки
. Ответ дайте в квадратных сантиметрах.
Решение: Первый способ по формуле для площади трапеции.
(см2)
Второй способ (достроим до прямоугольника):
(см2 )
S1 = (см2 )
S2 = (см2 )
S3 = (см2 )
Ответ: 18
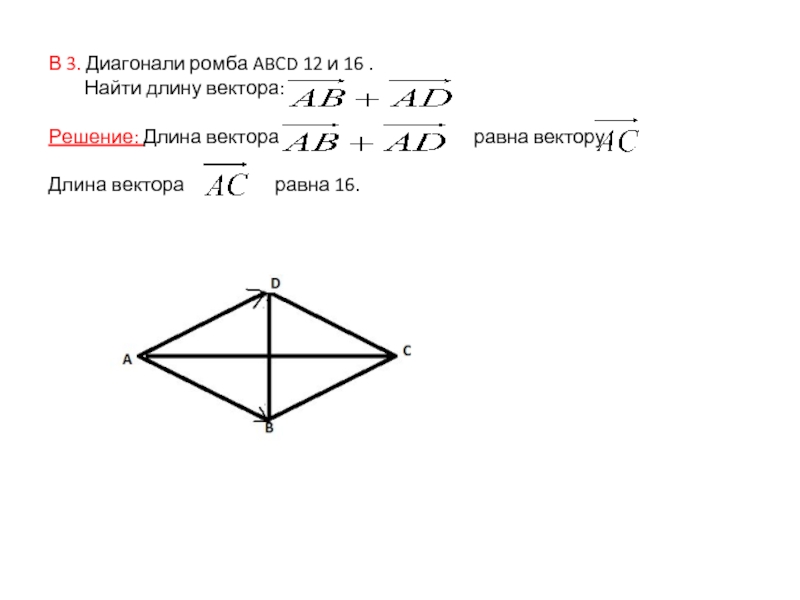
Слайд 7В 3. Диагонали ромба ABCD 12 и 16 .
Найти длину вектора:
Решение: Длина вектора
равна вектору
Длина вектора равна 16.
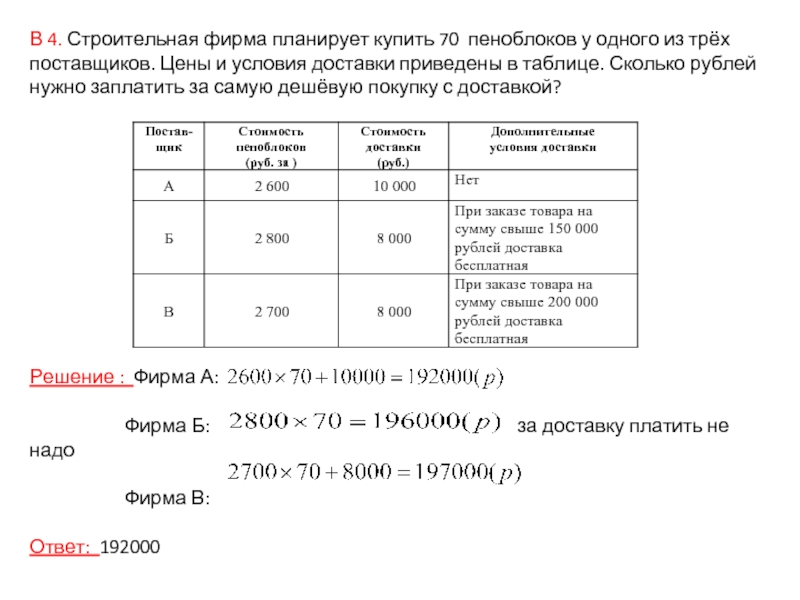
Слайд 8В 4. Строительная фирма планирует купить 70 пеноблоков у одного
из трёх поставщиков. Цены и условия доставки приведены в таблице.
Сколько рублей нужно заплатить за самую дешёвую покупку с доставкой?
Решение : Фирма А:
Фирма Б: за доставку платить не надо
Фирма В:
Ответ: 192000
Слайд 9В 4. В магазине одежды объявлена акция: если покупатель приобретает
товар на сумму свыше 10000 рублей, он получает скидку на
следующую покупку в размере 10% уплаченной суммы. Если покупатель участвует в акции, он теряет право возвратить товар в магазин. Покупатель В. Хочет приобрести куртку ценой 9300 рублей, рубашку ценой 1800 рублей и перчатки ценой 1200 рублей. В каком случае В. Заплатит за покупку меньше всего:
В. купит все три товара сразу.
В. купит сначала куртку и рубашку, а потом перчатки со скидкой.
В. купит сначала куртку и перчатки, а потом рубашку со скидкой.
В ответ запишите, сколько рублей В.заплатит за покупку в этом случае.
Решение:
Все три товара сразу:
Куртка и рубашка:
Перчатки:
Итого:
Куртка и перчатки:
Рубашка :
Итого:
Ответ: 11190
Слайд 10
В 5. Найдите корень уравнения :
Решение:
X-3=23 X-3= 8 X=11
Ответ: 11
В 5. Решите уравнение: В ответе напишите наименьший положительный корень.
Решение:
И далее при возрастании к, x тоже будет расти.
Ответ: 0,5
Слайд 11В 5. Решите уравнение
Если уравнение имеет более одного корня, в ответе запишите меньший из них.
Решение:
Ответ: 6
В 6. Треугольник АВС вписан в окружность с центром О. Найдите угол ВОС, если угол ВАС равен .
Решение: Угол ВАС- вписанный угол, который опирается на дугу СВ. Угол ВОС- центральный угол, который опирается на ту же дугу. По теореме о вписанном угле, он равен половине градусной меры дуги СВ, значит дуга СВ = , значит угол ВОС =
как центральный угол, опирающийся на дугу СВ.
Ответ: 64
Слайд 12В 6. В треугольнике АВС угол С =
АD и BE
– биссектрисы, пересекающиеся в точке О. Найдите угол АОВ, ответ
дайте в градусах.
Решение:
Ответ: 119
, если
Решение: По основному тригонометрическому тождеству
С учетом условия
,выбираем ответ
Ответ: - 0,8
Слайд 14В 7. Найдите значение выражения:
Решение:
Ответ: 7
В 7. Найдите значение
выражения:
Решение:
Ответ: 1
Используем:
Слайд 15В 8. На рисунке изображен график дифференцируемой функции
. На
оси абсцисс отмечены 9 точек: .Среди этих точек найдите все точки, в которых производная функции отрицательна. В ответе укажите количество найденных точек.
Решение: Известно, что промежутки возрастания дифференцируемой функции соответствуют неотрицательной производной, а убывания- неположительной производной. Значит точки, в которых производная функции отрицательна, должны лежать на промежутках убывания функции. Это точки .
Но точки соответствуют нулевой производной. Значит в ответе мы укажем количество точек 3.
Ответ: 3
является касательной к графику функции
.Найдите абсциссу точки касания.
Решение: Значение производной в точке касания равно угловому коэффициенту касательной (из уравнения касательной). Найдем производную функции и составим уравнение для поиска абсциссы точки касания.
Значит с таким угловым коэффициентом к данной функции можно провести две касательные. Одна с точкой касания , а другая с
Проверим, какая из точек удовлетворяет нашим условиям.
Точка касания должна быть общей и для касательной и для функции
Слайд 17Проверим
Значит точка (-1,-7) является общей точкой для этих функций.
Вторую точку можно не проверять, так как через данную точку
можно провести только одну прямую с угловым коэффициентом
Ответ: -1.
Слайд 18В 9. Диагонали АС основания правильной четырехугольной пирамиды SABCD равны
6. Высота пирамиды SO равна 4. Найдите длину бокового ребра
SB.
Решение: Боковое ребро SB является гипотенузой прямоугольного треугольника SOB, в котором известен катет SO=4. Осталось найти катет OB и тогда можно будет применить теорему Пифагора. Так как по условию пирамида правильная , значит в основании ее лежит квадрат, у которого диагонали равны и в точке пересечения делятся пополам. Значит,
OB=
Применяя теорему Пифагора получаем:
Ответ: 5
Слайд 19В 9. Найдите угол ABD, прямоугольного параллелепипеда, для которого AB=5,
AD=4, AA1 =3. Ответ дайте в градусах.
Решение:
является прямоугольным, так как по теореме о 3-х перпендикулярах. Нам известен катет BA= 5. По теореме Пифагора из прямоугольного , можно найти
Значит в рассматриваемом оба катета по 5,
значит треугольник равнобедренный и
прямоугольный . Оба острых угла такого треугольника по
Ответ: 45
Замечание: Можно решить эту задачу через тригонометрические функции для искомого угла. В таком случае, например тангенс угла ABD1 будет равен единице. Отсюда мы бы также нашли сам угол.
Слайд 20В 10. В сборнике билетов по биологии всего 25 билетов,
в двух из них встречается вопрос о грибах. На экзамене
школьнику достается один случайно выбранный билет из этого сборника. Найдите вероятность того, что в этом билете не будет вопроса о грибах.
Решение: Вероятность такого события будем искать по формуле ,
где - общее число исходов испытания, - число интересующих нас исходов.
Проводится испытание- школьник достает 1 билет из 25. Всего возможно 25 исходов. Из них нас интересует 23 исхода, значит
Ответ: 0,92
В 10. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 8 очков. Результат округлите до сотых.
Решение: При бросании двух костей можно получить 36 исходов. Нас интересуют исходы : 4+4, 5+3, 3+5, 2+6, 6+2, то есть всего 5 исходов.
Ответ: 0,14
Слайд 21В 11. Объем первого цилиндра 12 м3. У второго цилиндра
высота в три раза больше, а радиус основания в два
раза меньше, чем у первого. Найдите объем второго цилиндра (в м3 ).
Решение:
Имеем два цилиндра. Пусть R- радиус основания первого цилиндра, h- его высота. Значит
Значит объем второго цилиндра составляет объема первого.
Ответ: 9
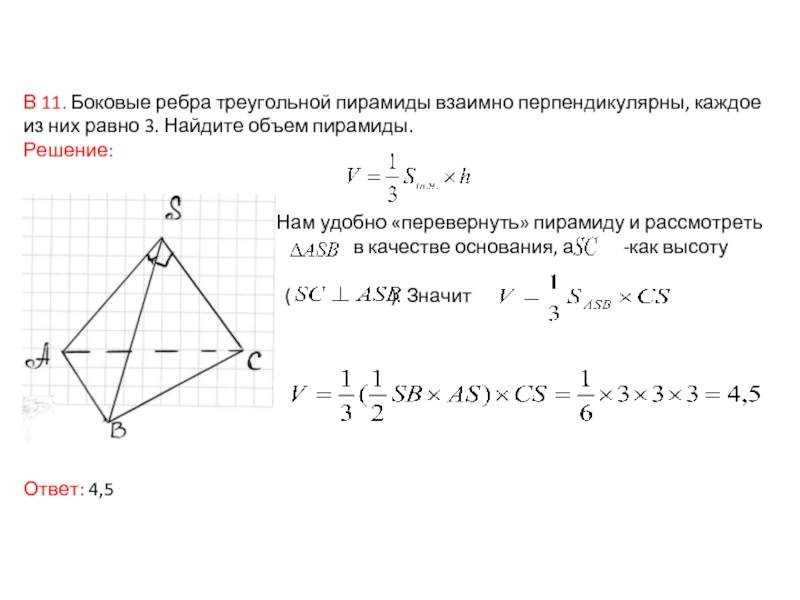
Слайд 22В 11. Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое из
них равно 3. Найдите объем пирамиды.
Решение:
Нам удобно «перевернуть» пирамиду и рассмотреть
в качестве основания, а -как высоту
( ). Значит
Ответ: 4,5
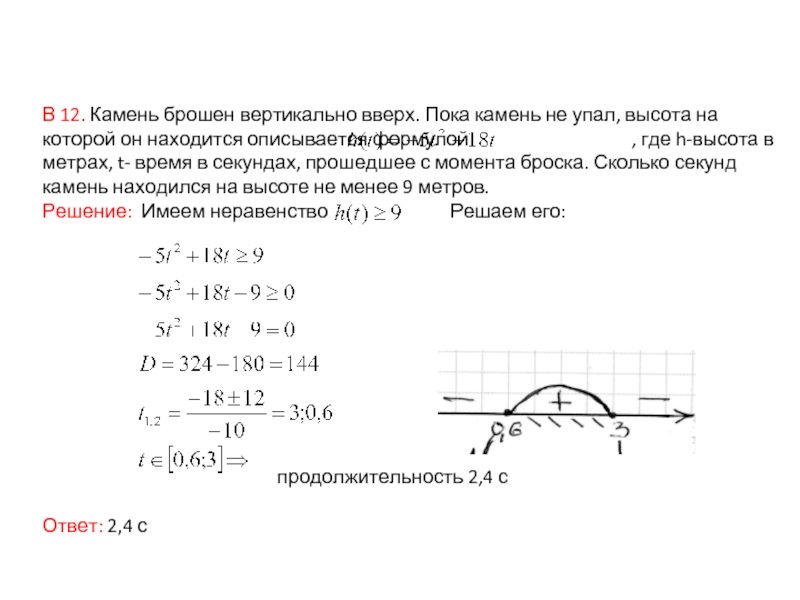
Слайд 23В 12. Камень брошен вертикально вверх. Пока камень не упал,
высота на которой он находится описывается формулой
, где h-высота в метрах, t- время в секундах, прошедшее с момента броска. Сколько секунд камень находился на высоте не менее 9 метров.
Решение: Имеем неравенство Решаем его:
продолжительность 2,4 с
Ответ: 2,4 с
Слайд 24В 12. По закону Ома для полной цепи сила тока,
измеряемая в амперах, равна
, где - ЭДС источника (в вольтах), r= 1 Ом- внутреннее сопротивление, R- сопротивление цепи (в Омах). При каком наименьшем сопротивлении цепи сила тока будет составлять не более 20% от силы тока короткого замыкания ?
Решение: Задача сводится к решению неравенства
Ответ: 4
Слайд 25В 12. Мяч бросили под углом к
плоской горизонтальной поверхности земли. Время полета мяча (в секундах) определяется
по формуле
При каком наименьшем значении угла (в градусах) время полета будет не меньше 3 секунд, если мяч бросают с начальной скоростью ? Считайте, что
Решение: Задача сводится к решению неравенства на интервале
при заданных значениях начальной скорости и ускорения свободного падения.
Ответ: 30
Слайд 26В 13. Весной катер идет против течения реки в
раза медленнее, чем по течению. Летом течение становится на
медленнее. Поэтому летом катер идет против течения в раза медленнее, чем по течению. Найдите скорость течения весной (в ).
Решение: Обозначим V км/ч- собственную скорость катера, X км/ч - скорость течения. Весной отношение скоростей против течения и по течению можно записать в виде равенства , а летом
Имеем систему уравнений:
Выражаем V из первого уравнения: V= 4x, подставляем во второе уравнение и получаем уравнение 4x+5=5x, откуда x=5.
Скорость течения 5 км/ч
Ответ: 5
Слайд 27В 13. Поезд, двигаясь равномерно со скоростью 60 км/ч, проезжает
мимо лесополосы, длина которой равна 400 метров, за 1 минуту.
Найти длину поезда в метрах.
Решение: Сначала выразим скорость поезда в м/с
60 км/ч = За 60 секунд точка ,расположенная в самом
начале состава пройдет расстояние равное сумме длины поезда и длины лесоповала.
Точка двигается со скоростью , значит
Ответ: 600
Слайд 28В 13. Виноград содержит 90% влаги, а изюм 5%. Сколько
килограммов винограда требуется для получения 20 килограммов изюма?
Решение: Виноград
Изюм
90%влага 10% остальное 5% влага 95% остальное
При высушивании масса «остального»остается неизменным. В 20 кг изюма эта масса равна: , а в винограде эта масса составляет 10%, значит общая масса винограда
Решение: 190
Слайд 29В 14. Найдите наибольшее значение функции
на отрезке
Решение:
Ответ: 1
Слайд 30В 14. Найдите точку минимума функции
Решение:
3)
x=4- точка минимума
Ответ: 4