Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ЕГЭ по математике - подготовка
Содержание
- 1. ЕГЭ по математике - подготовка
- 2. При решении задач с кратким ответом Единого
- 3. Слайд 3
- 4. Задание №1.Характеристика задания Задача на вычисление, моделирующая
- 5. Сырок стоит 7 руб. 40 коп. Какое
- 6. Задание №2.Характеристика задания Задача на вычисление, моделирующая
- 7. Слайд 7
- 8. Задание №3.Характеристика задания Задача на чтение графика
- 9. Слайд 9
- 10. Задание №4.Характеристика задания Текстовая задача (возможно, с
- 11. Слайд 11
- 12. Задание №5.Характеристика задания Планиметрическая задача на нахождение
- 13. Найдите площадь квадрата, изображенного на клетчатой бумаге
- 14. Задание №6.Характеристика задания Задача по теории вероятности.Для
- 15. Слайд 15
- 16. Задание №7.Характеристика задания Несложное рациональное, показательное, тригонометрическое
- 17. Найдите корень уравнения: ПроверкаПример заданияОтвет:
- 18. Задание №8.Характеристика задания Планиметрическая задача, связанная с
- 19. Слайд 19
- 20. Задание №9.Характеристика задания Задание на выполнение действий с функциямии производными функций, исследование функций.
- 21. Слайд 21
- 22. Задание №10.Характеристика задания Задание по стереометрии на
- 23. Слайд 23
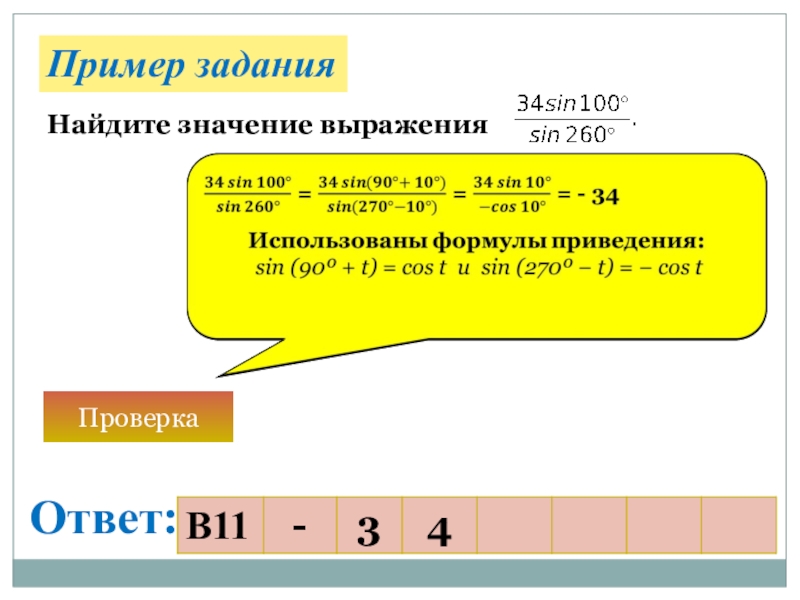
- 24. Задание №11.Характеристика задания Задача на вычисление значения
- 25. Найдите значение выраженияПроверкаПример заданияОтвет:
- 26. Задание №12.Характеристика задания Текстовое задание на анализ
- 27. Слайд 27
- 28. Задание №13.Характеристика задания Стереометрическая задача на нахождение
- 29. Слайд 29
- 30. Задание №14.Характеристика задания Текстовая задача (на движение, работу, проценты, прогрессию), сводящаяся к составлению и решению уравнения.
- 31. Пример задания
- 32. Задание №15.Характеристика задания Задание на вычисление с
- 33. ПроверкаПример заданияОтвет:
- 34. Еще есть время подготовиться!Скоро ЕГЭ!
- 35. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2При решении задач с кратким ответом Единого государственного экзамена и
проверке важно помнить:
Проверка ответов осуществляется компьютером ПОСЛЕ СКАНИРОВАНИЯ БЛАНКА ОТВЕТОВ
И СОПОСТАВЛЕНИЯ РЕЗУЛЬТАТОВ СКАНИРОВАНИЯ С ПРАВИЛЬНЫМИ ОТВЕТАМИОТВЕТОМ К ЗАДАЧЕ МОЖЕТ БЫТЬ ТОЛЬКО ЦЕЛОЕ ЧИСЛО ИЛИ КОНЕЧНАЯ ДЕСЯТИЧНАЯ ДРОБЬ. ОТВЕТ, ЗАФИКСИРОВАННЫЙ В ИНОЙ ФОРМЕ, БУДЕТ РАСПОЗНАН КАК НЕПРАВИЛЬНЫЙ.
ЕДИНИЦЫ ИЗМЕРЕНИЯ (В КАКИХ ИМЕННО ЕДИНИЦАХ ДОЛЖЕН БЫТЬ ДАН ОТВЕТ, УКАЗЫВАЕТСЯ В УСЛОВИИ ЗАДАЧИ) В БЛАНКЕ ОТВЕТОВ ПИСАТЬ НЕ НУЖНО, В ПРОТИВНОМ СЛУЧАЕ СКАНЕР,ВЕРОЯТНО, РАСПОЗНАЕТ ОТВЕТ КАК НЕПРАВИЛЬНЫЙ.
Задания уровня В – задания с кратким ответом
Слайд 4Задание №1.
Характеристика
задания
Задача на вычисление, моделирующая реальную или близкую
к реальной ситуацию.
Для решения задачи достаточно уметь выполнять арифметические действия
с целыми числами и дробями, делать оценку и прикидку при практических расчетахСлайд 5Сырок стоит 7 руб. 40 коп. Какое наибольшее число сырков
можно купить на 70 рублей?
Проверка
7 руб 40 коп=7,4 руб
70:7,4≈
9,45…Пример задания
Ответ:
Слайд 6Задание №2.
Характеристика
задания
Задача на вычисление, моделирующая реальную или близкую
к реальной ситуацию.
Для решения задачи достаточно уметь выполнять арифметические действия
с дробями, знать, что такое доли и отношения, понимать, что процент – это одна сотая часть числа, уметь делать прикидку и оценку при практических расчетахСлайд 7
Цена
на электрический чайник была повышена на 24% и составила 1860 рублей. Сколько рублей стоил товар до повышения цены? Проверка
100%+24%=124%
1860руб -124%
Хруб – 100%
Пример задания
Слайд 8Задание №3.
Характеристика
задания
Задача на чтение графика функции (диаграммы), моделирующая
реальную или близкую к реальной ситуацию.
Простейшее задание на считывание информации,
представленной в виде диаграммы или графика, возможно, требующее незначительных вычислении.Слайд 9
На рисунке жирными точками показана среднесуточная температура воздуха в Бресте каждый день с 6 по 19 июля 1981 года. По горизонтали указываются числа месяца, по вертикали — температура в градусах Цельсия. Для наглядности жирные точки соединены линией. Определите по рисунку разность между наибольшей и наименьшей среднесуточными температурами за указанный период. Ответ дайте в градусах Цельсия.?
Проверка
Наибольшая температура за указанный период 26 градусов Цельсия, наименьшая 16. Обратите внимание, что цена одного деления (по вертикали) равна 1 градусу. Разность температур составляет 26-16=10.
Пример задания
Ответ:
Слайд 10Задание №4.
Характеристика
задания
Текстовая задача (возможно, с табличными данными) на
оптимальное
решение, связанная с анализом практической деятельности И моделирующая реальную или
близкую к реальной ситуацию. Требуется аккуратность при записи ответа.Слайд 11
Проверка
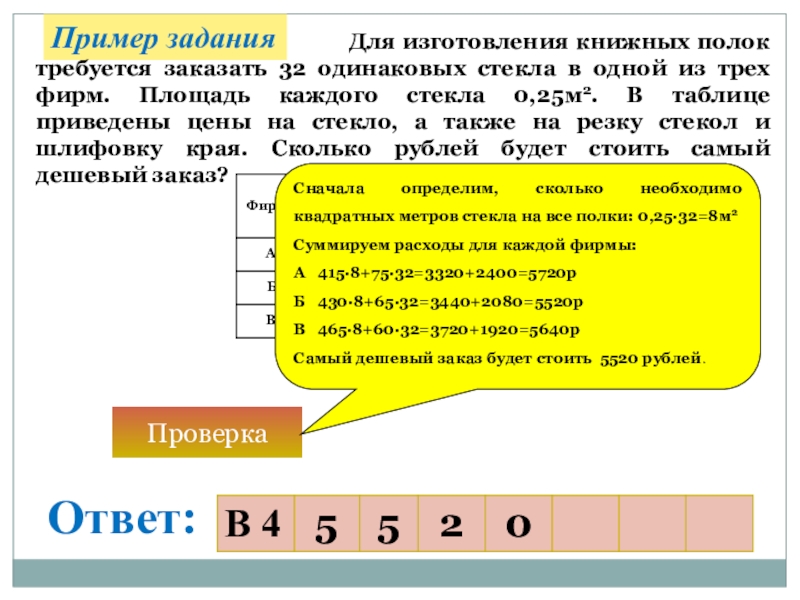
Сначала определим, сколько необходимо квадратных метров стекла на все полки: 0,25∙32=8м2
Суммируем расходы для каждой фирмы:
А 415∙8+75∙32=3320+2400=5720р
Б 430∙8+65∙32=3440+2080=5520р
В 465∙8+60∙32=3720+1920=5640р
Самый дешевый заказ будет стоить 5520 рублей.
Пример задания
Ответ:
Для изготовления книжных полок требуется заказать 32 одинаковых стекла в одной из трех фирм. Площадь каждого стекла 0,25м2. В таблице приведены цены на стекло, а также на резку стекол и шлифовку края. Сколько рублей будет стоить самый дешевый заказ?
Слайд 12Задание №5.
Характеристика
задания
Планиметрическая задача на нахождение геометрических величин (длин,
углов,).
Задание на вычисление площади треугольника, четырехугольника, круга и его частей,
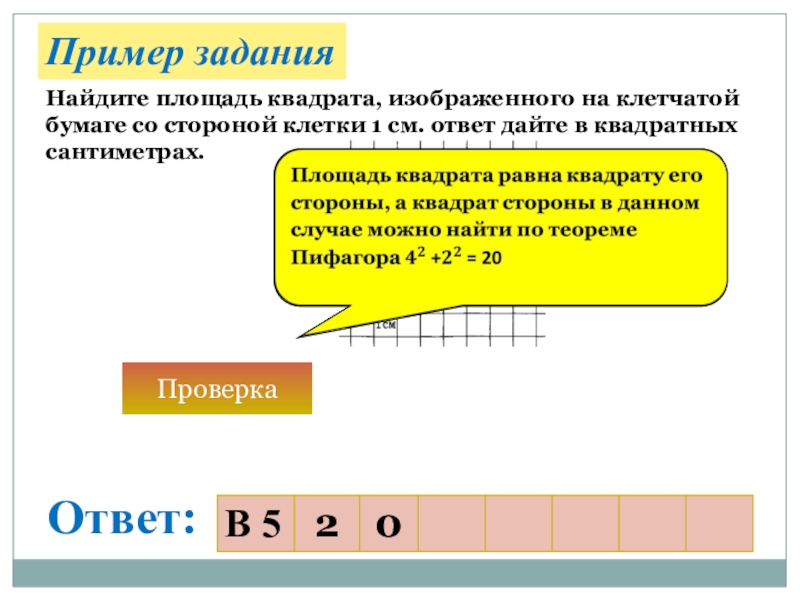
в том числе по данным рисунка, представляющего собой изображение фигуры на координатной плоскости или клетчатой бумаге (сетке)Слайд 13Найдите площадь квадрата, изображенного на клетчатой бумаге со стороной клетки
1 см. ответ дайте в квадратных сантиметрах.
Проверка
Пример задания
Ответ:
Слайд 14Задание №6.
Характеристика
задания
Задача по теории вероятности.
Для решения достаточно уметь
находить отношение числа благоприятных для данного события исходов к числу
всех равновозможных исходов.Слайд 15
В группе туристов 30 человек. Их вертолётом в несколько приёмов забрасывают в труднодоступный район по 6 человек за рейс. Порядок, в котором вертолёт перевозит туристов, случаен. Найдите вероятность того, что турист П. полетит первым рейсом вертолёта.
Проверка
Всего рейсов 30 : 6 = 5
Попасть на первый рейс (равно как и на второй и на любой имеющийся) – один шанс из пяти .
Вероятность Р = 1 : 5 = 0,2.
Пример задания
Ответ:
Слайд 16Задание №7.
Характеристика
задания
Несложное рациональное, показательное, тригонометрическое или
иррациональное. Уравнение сводится
в одно действие к линейному или квадратному ( в последнем
случае в зависимости от условия в ответе указать только один из корней – меньший или больший).Слайд 18Задание №8.
Характеристика
задания
Планиметрическая задача, связанная с нахождением
геометрических величин. Для
решения задачи достаточно знать основные формулы и теоремы планиметрии.
Слайд 19
Площадь треугольника ABC равна 4. DE — средняя линия. Найдите площадь треугольника CDE.
Проверка
Треугольник CDE подобен треугольнику CAB. Коэффициент подобия равен отношению подобных сторон. Отрезок DE — средняя линия, ее длина равна половине основания. Поэтому коэффициент подобия равен 0,5. Площади подобных фигур относятся как квадрат
коэффициента подобия. Тогда S = ¼ •4 =1
Пример задания
Ответ:
Слайд 20Задание №9.
Характеристика
задания
Задание на выполнение действий с функциями
и производными
функций, исследование функций.
Слайд 21
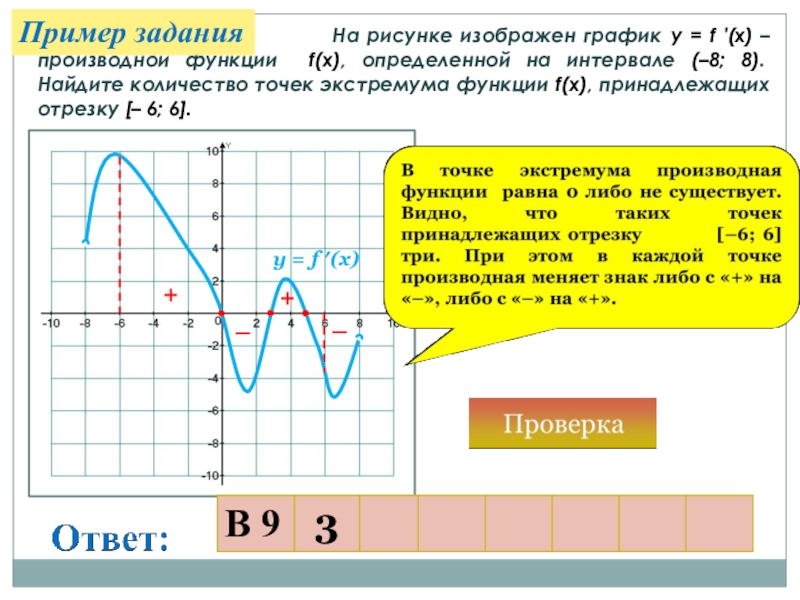
На рисунке изображен график у = f ′(x) – производной функции f(x), определенной на интервале (–8; 8). Найдите количество точек экстремума функции f(x), принадлежащих отрезку [– 6; 6].
+
–
–
+
у = f ′(x)
Пример задания
Слайд 22Задание №10.
Характеристика
задания
Задание по стереометрии на применение основных формул,
связанных с
вычислением площадей поверхностей или объемов многогранников или тел вращения,
в том числе вписанных или описанных около других многогранников или тел вращения.Слайд 23
Из
единичного куба вырезана правильная четырехугольная призма со стороной основания 0,6 и боковым ребром 1. Найдите площадь поверхности оставшейся части куба.Проверка
Площадь поверхности получившегося многогранника равна сумме площадей боковых граней куба со стороной 1 и
призмы со сторонами 1; 0,6; 0,6 и
2 площади основания куба с вырезанными основаниями призмы:
S = 4•1•1+ 4•0,6•1 + 2(1•1 – 0,6•0,6) = 7,68
Пример задания
Ответ:
Слайд 24Задание №11.
Характеристика
задания
Задача на вычисление значения числового или
буквенного выражения.
Для решения достаточно уметь выполнять действия с числами, знать определение
и простейшие свойства степеней, корней, логарифмов, синуса, косинуса, тангенса.Слайд 26Задание №12.
Характеристика
задания
Текстовое задание на анализ практической
ситуации, моделирующее
реальную или близкую к реальной ситуацию (экономические, физические, химические процессы.
По условию задачи требуется составить уравнение или неравенство, сводимое к линейному или квадратному.Слайд 27
После
дождя уровень воды в колодце может повыситься. Мальчик измеряет время t падения небольших камешков в колодец и рассчитывает расстояние до воды по формуле , где h — расстояние в метрах, t — время падения в секундах. До дождя время падения камешков составляло 0,6 с. Насколько должен подняться уровень воды после дождя, чтобы измеряемое время изменилось на 0,2 с? Ответ выразите в метрах.Проверка
Пример задания
Ответ:
Слайд 28Задание №13.
Характеристика
задания
Стереометрическая задача на нахождение
геометрических величин. Для
решения достаточно знать свойства правильных пирамид и призм, формулы площадей
поверхности и объемов многогранников и тел вращения.Слайд 29
Через основание треугольной призмы проведена плоскость, параллельно боковому ребру. Объем отсеченной треугольной призмы равен 5. Найдите объем исходной призмы.
Проверка
Пример задания
Ответ:
Слайд 30Задание №14.
Характеристика
задания
Текстовая задача (на движение, работу,
проценты, прогрессию),
сводящаяся к составлению и решению уравнения.
Слайд 31Пример задания
Первый сплав содержит 10% меди, второй – 40% меди. Масса второго сплава больше массы первого на 3 килограмма. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третьего сплава. Ответ дайте в кг.
Проверка
Проследим за количеством меди в каждом сплаве.
Пусть х(кг) масса первого сплава, (х + 3)кг масса второго сплава.
Меди в первом сплаве 10%, значит масса меди в первом сплаве 0,1х.
Меди во втором сплаве 40%, значит масса меди во втором сплаве 0,4(х + 3).
Масса третьего сплава (х + х + 3).
Меди в третьем сплаве 30%, значит масса меди в третьем сплаве 0,3 (2х +3).
Составим уравнение, исходя из количества меди в каждом сплаве
0,1х + 0,4 (х + 3) = 0,3 ( 2х + 3)
-0,1х = -0,3
х = 3
3(кг) масса первого сплава, масса третьего сплава 9 кг.
Ответ: