Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Многоликая симметрия
Содержание
- 1. Многоликая симметрия
- 2. ЦЕЛЬ РАБОТЫ: Изучить тему «Симметрия»Исследовать вопрос
- 3. ГИПОТЕЗА: Зачем человеку нужно знать о симметрии? Почему симметрия буквально пронизывает весь окружающий нас мир?
- 4. ЗАДАЧИ ИССЛЕДОВАНИЯ:1. Раскрыть смысл основных понятий симметрии.2.Показать, что природа – это мир симметрии.
- 5. МЕТОДЫ ИССЛЕДОВАНИЯ: изучение литературы; сопоставление существенных признаков; анализ, сравнение, обобщение.
- 6. СОДЕРЖАНИЕ. 1.Введение 2.Понятие симметрии. 3.Виды симметрии.4.Симметрия в
- 7. О симметрия! Гимн тебе пою! Тебя повсюду
- 8. ВВЕДЕНИЕ Тема моей научно – исследовательской работы
- 9. Что же такое симметрия? Какой глубокий смысл
- 10. ЧТО ТАКОЕ СИММЕТРИЯ? Симметрия (от греческого
- 11. Симметрия – это уравновешенность, упорядоченность, красота, совершенство.
- 12. ВИДЫ СИММЕТРИИа) симметрия относительно точки (центральная симметрия);
- 13. СИММЕТРИЧНОСТЬ ТОЧЕК ОТНОСИТЕЛЬНО ЦЕНТРА
- 14. СИММЕТРИЧНОСТЬ ФИГУРЫ ОТНОСИТЕЛЬНО ЦЕНТРАABCDO
- 15. Симметричность точек относительно прямой A1AaOA A1
- 16. Симметричность фигуры относительно прямойАDBCabcОпределениеФигура называется симметричной относительно
- 17. СИММЕТРИЯ ОТНОСИТЕЛЬНО ПЛОСКОСТИ (ЗЕРКАЛЬНАЯ СИММЕТРИЯ)-это такое
- 18. ПОВОРОТ. Преобразование, при
- 19. ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС. Преобразование, при котором
- 20. СКОЛЬЗЯЩАЯ СИММЕТРИЯ. Скользящей симметрией называется такое
- 21. ДЛЯ ПРЕОБРАЗОВАНИЙ СИММЕТРИИ ИМЕЮТ МЕСТО СЛЕДУЮЩИЕ СВОЙСТВА:
- 22. Итак, на плоскости мы имеем
- 23. СИММЕТРИЯ В ОКРУЖАЮЩЕМ НАС МИРЕ. РАДИА́ЛЬНАЯ
- 24. ОСЕВАЯ (БИЛАТЕРАЛЬНАЯ) СИММЕТРИЯ: ЖУКИ
- 25. ОСЕВАЯ (БИЛАТЕРАЛЬНАЯ) СИММЕТРИЯ: БАБОЧКИ
- 26. ПТИЦЫ
- 27. РЫБЫ
- 28. ГРИБЫ
- 29. ДЕРЕВЬЯ
- 30. МОРСКАЯ ЗВЕЗДА
- 31. МОРСКОЙ ЕЖ
- 32. ЦВЕТЫ
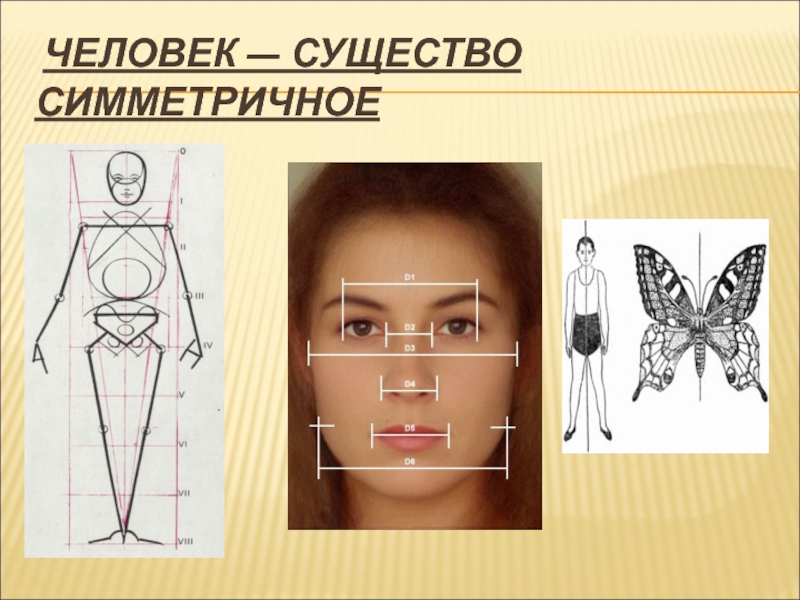
- 33. ЧЕЛОВЕК — СУЩЕСТВО СИММЕТРИЧНОЕ
- 34. СИММЕТРИЯ ЕСТЬ И В ТАКОМ ТВОРЕНИИ ПРИРОДЫ
- 35. «ГОЛУБЫЕ ОЗЕРА»
- 36. Слайд 36
- 37. Слайд 37
- 38. Слайд 38
- 39. СИММЕТРИЯ В АРХИТЕКТУРЕ
- 40. СИММЕТРИЯ В АРХИТЕКТУРЕ
- 41. Слайд 41
- 42. ПАРКЕТ
- 43. КОВАНЫЕ РЕШЕТКИ
- 44. ВЫШИВКАРазличные виды симметрий используются в декоративно-прикладном искусстве.
- 45. КОВРЫ
- 46. Слайд 46
- 47. Слайд 47
- 48. Слайд 48
- 49. Слайд 49
- 50. Слайд 50
- 51. Слайд 51
- 52. Слайд 52
- 53. ФИГУРЫ, СИММЕТРИЧНЫЕ ОТНОСИТЕЛЬНО ЦЕНТРА
- 54. ФИГУРЫ, СИММЕТРИЧНЫЕ ОТНОСИТЕЛЬНО ПРЯМОЙ
- 55. ЗАКЛЮЧЕНИЕСимметрия многолика. Она связана с упорядоченностью, пропорциональностью
- 56. ЛИТЕРАТУРА 1.Этот удивительно симметричный мир» –
- 57. Спасибо за внимание!
- 58. Скачать презентанцию
ЦЕЛЬ РАБОТЫ: Изучить тему «Симметрия»Исследовать вопрос «Симметрия в окружающем нас мире»Рассмотреть различные виды симметрии в природных объектах
Слайды и текст этой презентации
Слайд 2ЦЕЛЬ РАБОТЫ:
Изучить тему «Симметрия»
Исследовать вопрос «Симметрия в окружающем нас
мире»
Рассмотреть различные виды симметрии в природных объектах
Слайд 3ГИПОТЕЗА:
Зачем человеку нужно знать о симметрии?
Почему симметрия буквально
пронизывает весь окружающий нас мир?
Слайд 4ЗАДАЧИ ИССЛЕДОВАНИЯ:
1. Раскрыть смысл основных понятий симметрии.
2.Показать, что природа – это
мир симметрии.
Слайд 5МЕТОДЫ ИССЛЕДОВАНИЯ:
изучение литературы;
сопоставление существенных признаков;
анализ, сравнение, обобщение.
Слайд 6СОДЕРЖАНИЕ.
1.Введение
2.Понятие симметрии.
3.Виды симметрии.
4.Симметрия в математике.
5. Симметрия в окружающем
нас мире.
6. Заключение
7. Литература
Слайд 7
О симметрия!
Гимн тебе пою!
Тебя повсюду в мире узнаю.
Ты в Эйфелевой башне, в малой мошке,
Ты в елочке,
что у лесной дорожки. С тобою в дружбе и тюльпан, и роза,
И снежный рой – творение мороза!
Слайд 8ВВЕДЕНИЕ
Тема моей научно – исследовательской работы «Многоликая симметрия».
Эту
тему я выбрала потому, что с симметрией мы встречаемся везде
– в природе, архитектуре, искусстве, науке. Мне хочется глубже познакомиться с симметрией в математике и биологии, технике и архитектуре так как понятие симметрии широко используют все направления современной науки.Слайд 9Что же такое симметрия?
Какой глубокий смысл заложен в этом
понятии?
Почему симметрия буквально пронизывает весь окружающий нас мир?
Слайд 10ЧТО ТАКОЕ СИММЕТРИЯ?
Симметрия (от греческого symmetria - "соразмерность") -
понятие, означающее сохраняемость, повторяемость, "инвариантность" каких-либо особенностей структуры изучаемого объекта
при проведении с ним определенных преобразований.Слайд 12ВИДЫ СИММЕТРИИ
а) симметрия относительно точки (центральная симметрия);
б) симметрия
относительно прямой (осевая симметрия);
в) симметрия относительно плоскости (зеркальная симметрия);
г) Симметрия вращения (поворот)
д)Скользящая симметрия
Слайд 13СИММЕТРИЧНОСТЬ ТОЧЕК ОТНОСИТЕЛЬНО ЦЕНТРА
ОА1 =
ОА
A
O
A1
Определение
Точки A и A1 называются симметричными относительно точки О, если
О – середина отрезка AA1.Слайд 14СИММЕТРИЧНОСТЬ ФИГУРЫ ОТНОСИТЕЛЬНО ЦЕНТРА
A
B
C
D
O
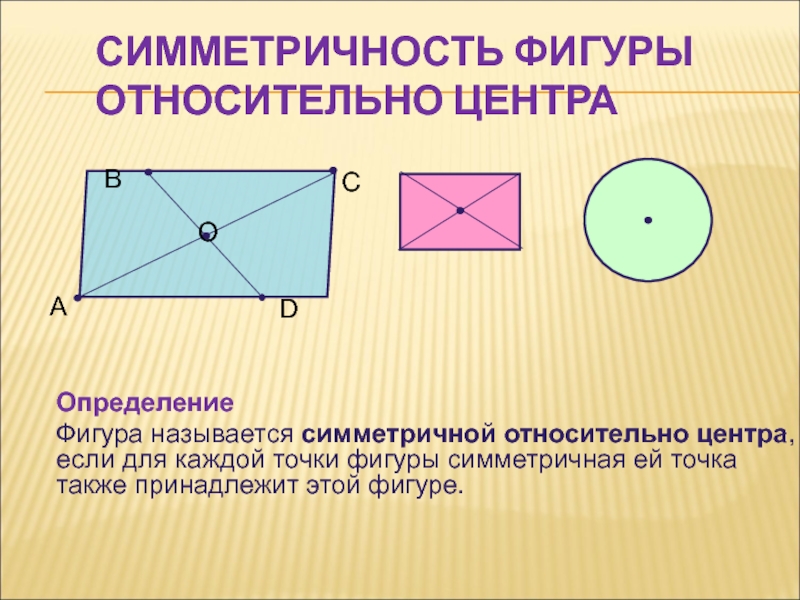
Определение
Фигура называется симметричной относительно центра, если для каждой точки фигуры
симметричная ей точка также принадлежит этой фигуре.Слайд 15Симметричность точек относительно прямой
A1
A
a
O
A A1
a
Т
AO =
OA1
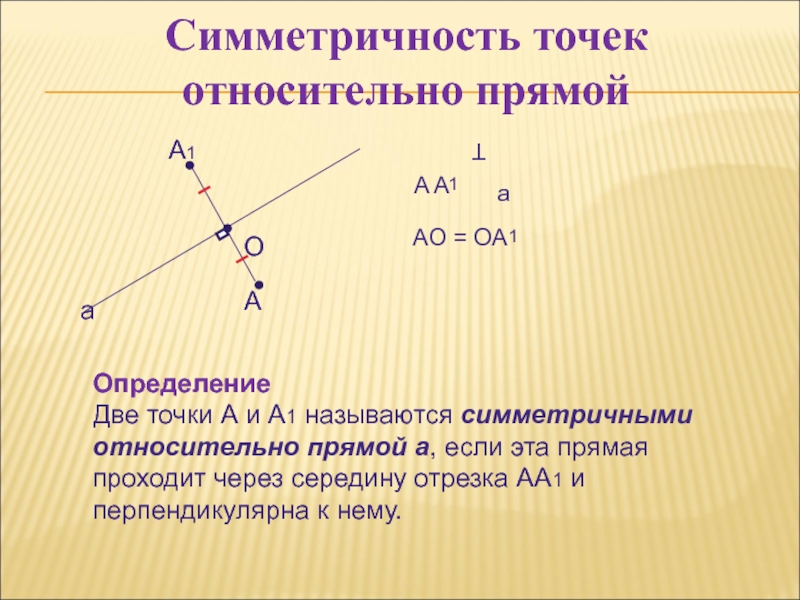
Определение
Две точки А и А1 называются симметричными относительно прямой
а, если эта прямая проходит через середину отрезка АА1 и перпендикулярна к нему.Слайд 16Симметричность фигуры относительно прямой
А
D
B
C
a
b
c
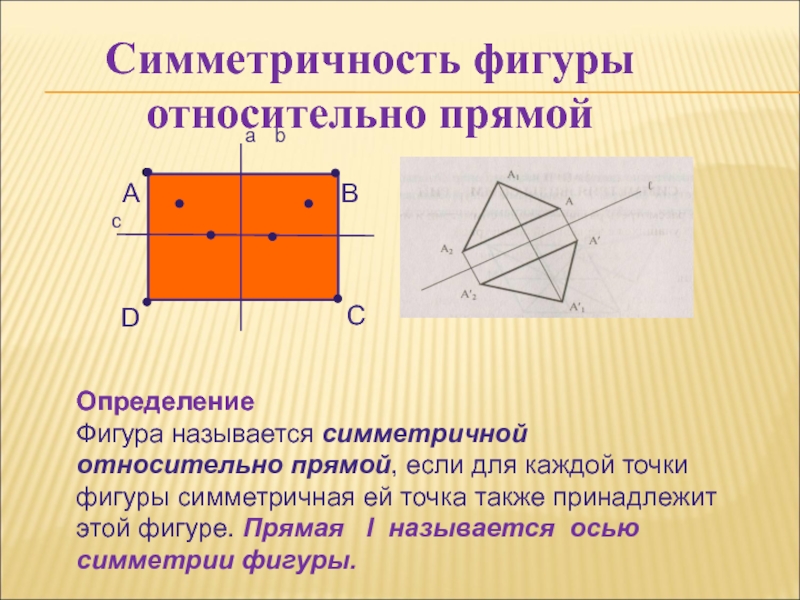
Определение
Фигура называется симметричной относительно прямой, если для
каждой точки фигуры симметричная ей точка также принадлежит этой фигуре.
Прямая l называется осью симметрии фигуры.Слайд 17 СИММЕТРИЯ ОТНОСИТЕЛЬНО ПЛОСКОСТИ (ЗЕРКАЛЬНАЯ СИММЕТРИЯ)-
это такое свойство геометрической фигуры,
когда любой точке, расположенной по одну сторону плоскости, всегда будет
соответствовать точка, расположенная по другую сторону плоскости, а отрезки, соединяющие эти точки, будут перпендикулярны плоскости симметрии и делятся ею пополам.Слайд 18 ПОВОРОТ.
Преобразование, при котором каждая точка А
фигуры (тела) поворачивается на один и тот же угол α
вокруг заданного центра О, называется вращением или поворотом плоскости. Точка О называется центром вращения, а угол α - углом вращения. Точка О является неподвижной точкой этого преобразования.Центральная симметрия есть поворот фигуры на 180°.
Слайд 19ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС.
Преобразование, при котором каждая точка фигуры перемещается
в одном и том же направлении на одно и то
же расстояние, называется параллельным переносом.Слайд 20СКОЛЬЗЯЩАЯ СИММЕТРИЯ.
Скользящей симметрией называется такое преобразование, при котором последовательно
выполняются осевая симметрия и параллельный перенос.
Слайд 21ДЛЯ ПРЕОБРАЗОВАНИЙ СИММЕТРИИ ИМЕЮТ МЕСТО СЛЕДУЮЩИЕ СВОЙСТВА:
отрезок переходит в равный
ему отрезок;
угол переходит в равный ему угол;
окружность переходит в равную
ей окружность;любой многоугольник переходит в равный ему многоугольник и т. д.
параллельные прямые переходят в параллельные, перпендикулярные в перпендикулярные.
Слайд 22 Итак, на плоскости мы имеем четыре вида движений,
переводящих фигуру F в равную фигуру F1:
параллельный перенос;
осевая симметрия (отражение
от прямой);поворот вокруг точки (частичный случай – центральная симметрия);
«скользящее» отражение.
Слайд 23СИММЕТРИЯ В ОКРУЖАЮЩЕМ НАС МИРЕ.
РАДИА́ЛЬНАЯ СИММЕ́ТРИЯ
(лучевая симметрия)- симметрия
по отношению к любым плоскостям, проходящим через продольную ось
тела животного.Билатера́льная симме́трия (двусторонняя симметрия) — симметрия зеркального отражения, при которой объект имеет одну плоскость симметрии, относительно которой две его половины зеркально симметричны.
Слайд 34СИММЕТРИЯ ЕСТЬ И В ТАКОМ ТВОРЕНИИ ПРИРОДЫ КАК ОТРАЖЕНИЕ В
ВОДЕ – ЕДИНСТВЕННЫЙ ПРИМЕР ГОРИЗОНТАЛЬНОЙ СИММЕТРИИ.
Слайд 55ЗАКЛЮЧЕНИЕ
Симметрия многолика.
Она связана с упорядоченностью, пропорциональностью и соразмерностью частей,
красотой и гармонией, с целесообразностью и полезностью.
Работая над проектом, я прикоснулась к загадочной математической красоте. Математика — это язык, язык природы. Не зная языка, вы не можете понять красоту окружающего мира.Но несомненно одно: Мир симметричен!
Слайд 56 ЛИТЕРАТУРА
1.Этот удивительно симметричный мир» – Л. Тарасов
2. «Толковый словарь»
- В.Даля
«Геометрия 7-9 класс» - Л. Атанасян
Малахов В.В. //
Журн. общ. биологии. 1977. Т.38. И.Г.Зенкевич “Эстетика урока математики”.
http://900igr.net/fotografii/geometrija/Simmetrija/O-simmetrii.html