Автор работы:
Окунев Дмитрий Олегович,
ученик 10 «А» класса
МОУ «Гимназия имени А.М. Горького»
Москаленского муниципального района
Омской области
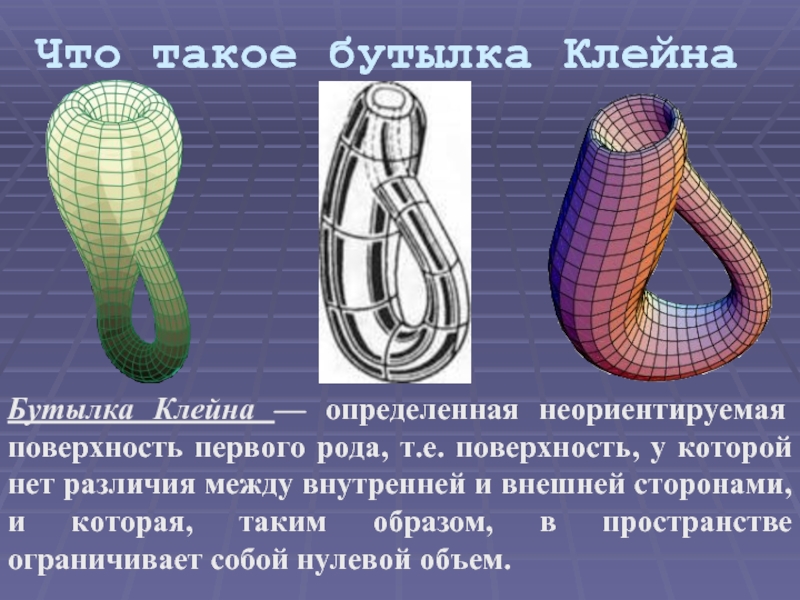
«Эта загадочная
Бутылка Клейна»
(исследовательская работа по математике)
Руководитель работы: Фабер Галина Николаевна,
учитель математики МОУ «Гимназия имени А.М. Горького»
Москаленского муниципального района
Омской области
Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация на тему Эта загадочная Бутылка Клейна
Презентация на тему Презентация на тему Эта загадочная Бутылка Клейна из раздела Математика. Доклад-презентацию можно скачать по ссылке внизу страницы. Эта презентация для класса содержит 8 слайдов. Для просмотра воспользуйтесь удобным проигрывателем, если материал оказался полезным для Вас - поделитесь им с друзьями с помощью социальных кнопок и добавьте наш сайт презентаций TheSlide.ru в закладки!
Слайды и текст этой презентации
Что такое бутылка Клейна
Бутылка Клейна — определенная неориентируемая поверхность первого рода, т.е. поверхность, у которой нет различия между внутренней и внешней сторонами, и которая, таким образом, в пространстве ограничивает собой нулевой объем.
История изобретения бутылки Клейна
Феликс Христиан Клейн – немецкий математик. Пытаясь доказать непротиворечивость геометрии Лобачевского, изобрёл открытие поразительной красоты - свою бутылку в 1882 г. Это блестящий и очень наглядный пример односторонней поверхности. В ней со всей полнотой проявился и талант математика, и дар выдающегося преподавателя.
Сравнительная характеристика бутылки Клейна и листа Мёбиуса
Таким образом, подтверждается выдвинутая гипотеза. Бутылка Клейна, подобно листу Мёбиуса является топологическим объектом. Значит, бутылка Клейна обладает топологическими свойствами.
Топологические свойства бутылки Клейна
1.«Хроматический номер»
2. Непрерывность
3. Ориентированность
Конструирование бутылки Клейна
Способ № 1. Получение бутылки Клейна из бумаги.
Способ № 2. Получение бутылки Клейна из стандартной пластмассовой бутылки.
Способ № 3. Получение бутылки Клейна из одного цилиндра.
Способ № 4. Получение бутылки Клейна из ткани.
Способ № 5. Получение бутылки Клейна склеиванием двух листов Мёбиуса.
Способ № 6. Получение бутылки Клейна из пластилина.
Применение бутылки Клейна
Бутылка Клейна и изготовление стёкол
Бутылку Клейна могут изготовить только высококвалифицированные стеклодувы. Но и они не смогут её изготовить в подлинном виде, так как место самопересечения будет запаяно. Но, не смотря на это, они отливают бутылки в качестве сувениров и даже соревнуются, у кого лучше и больше получилась бутылка.
Выступление в классе
Работа учащихся с моделями бутылки Клейна
Демонстрация свойств бутылки Клейна
Теги
