Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Графическое решение квадратных уравнений 8 класс
Содержание
- 1. Графическое решение квадратных уравнений 8 класс
- 2. -12-11ух321-23-3-2-3
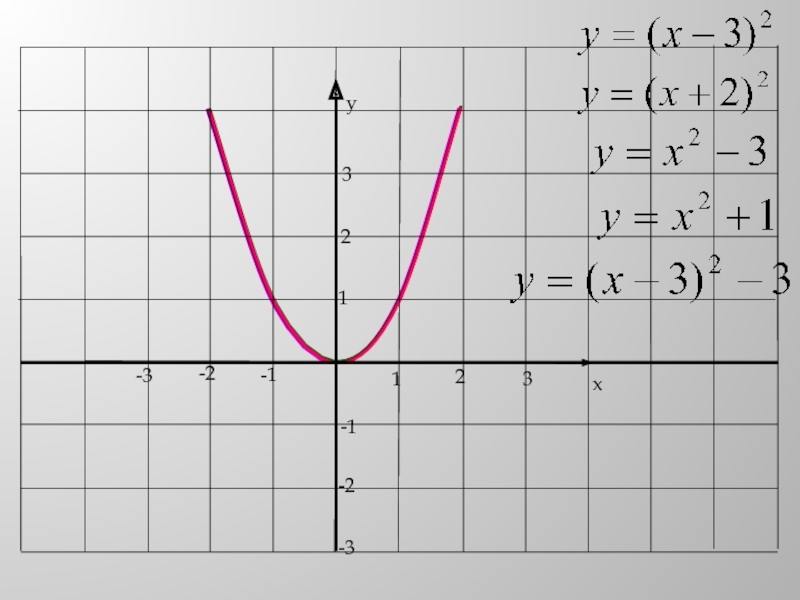
- 3. а) Укажите направление ветвей параболы
- 4. Слайд 4
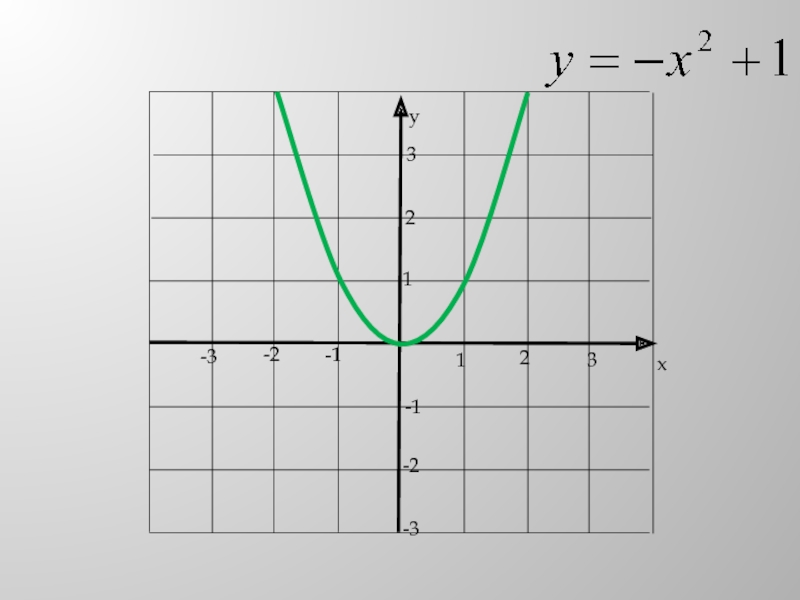
- 5. Слайд 5
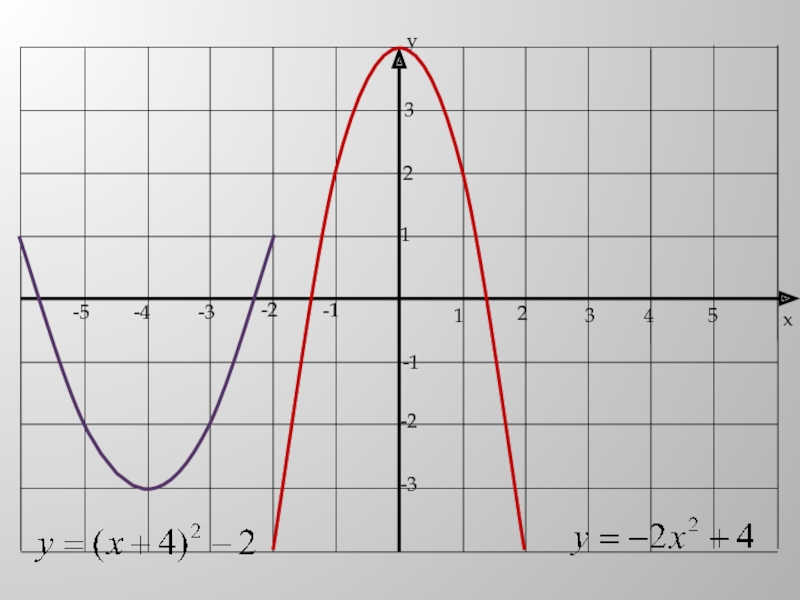
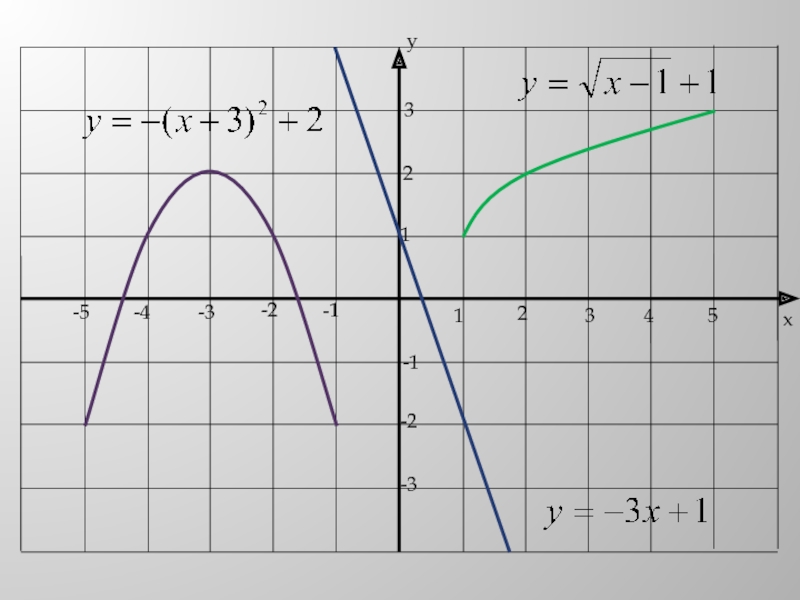
- 6. Слайд 6
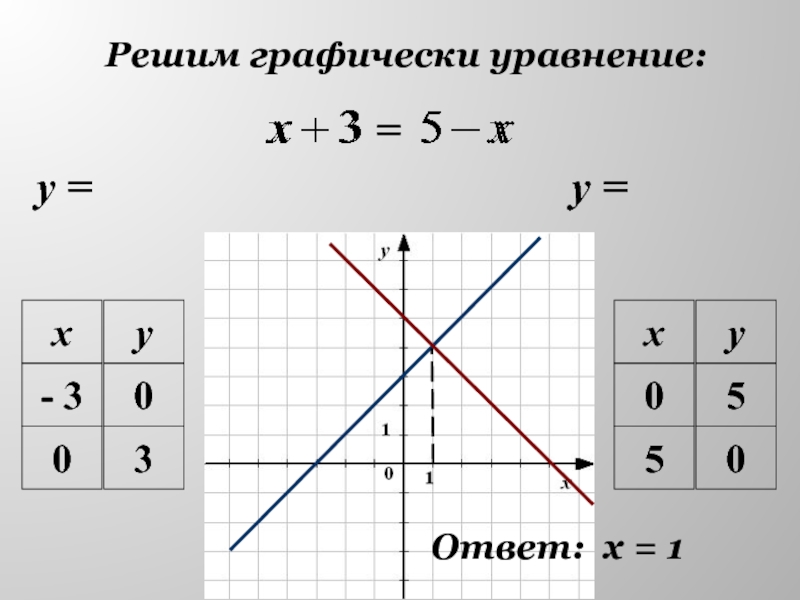
- 7. Решим графически уравнение:у =у =Ответ: х = 1
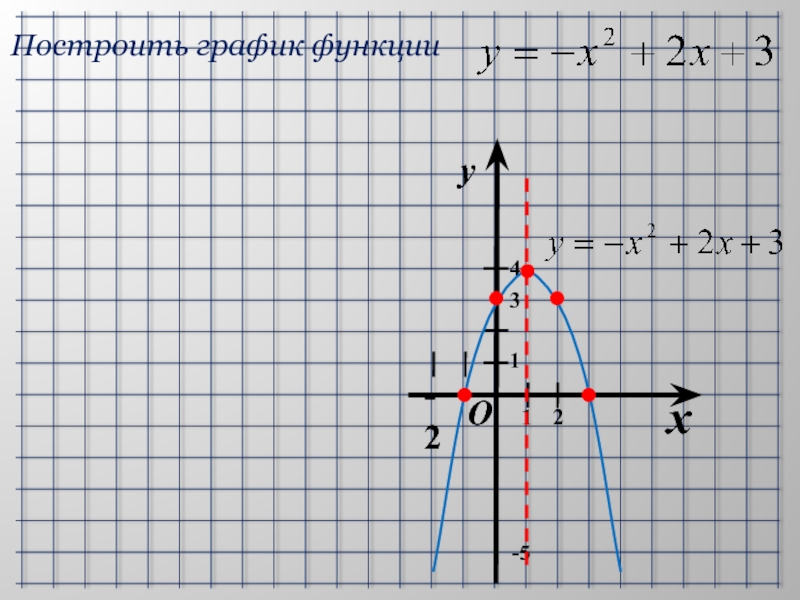
- 8. Построить график функцииНайдём координаты вершины параболы- ось симметрии параболы- вершина параболыДополнительные точки:
- 9. xy11-2-524O3Построить график функции
- 10. ОпределениеКвадратным уравнением называется уравнение вида ах2 +
- 11. Решить уравнение 1 способ
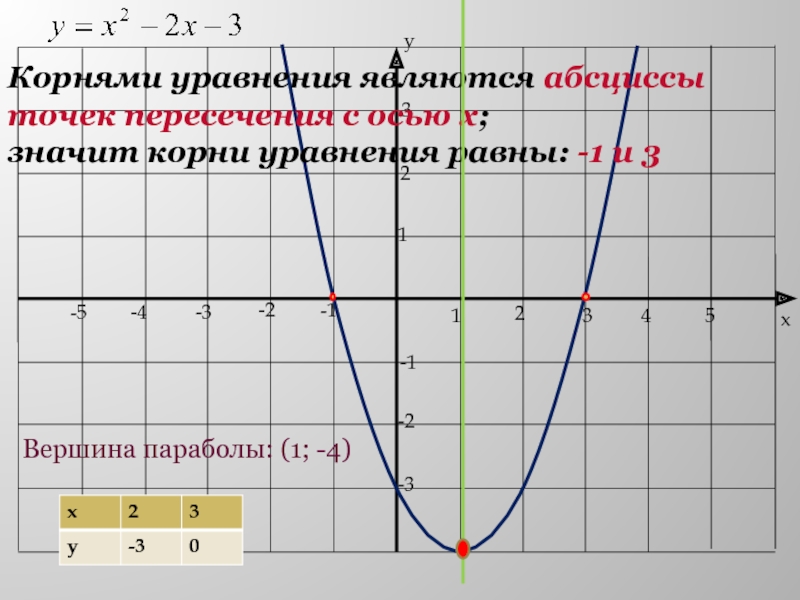
- 12. Вершина параболы: (1; -4)Корнями уравнения являются абсциссы
- 13. 2 способПреобразуем
- 14. 2ух45-2-211-376-1330Корнями уравнения являются абсциссы точек пересечения: -1 и 3
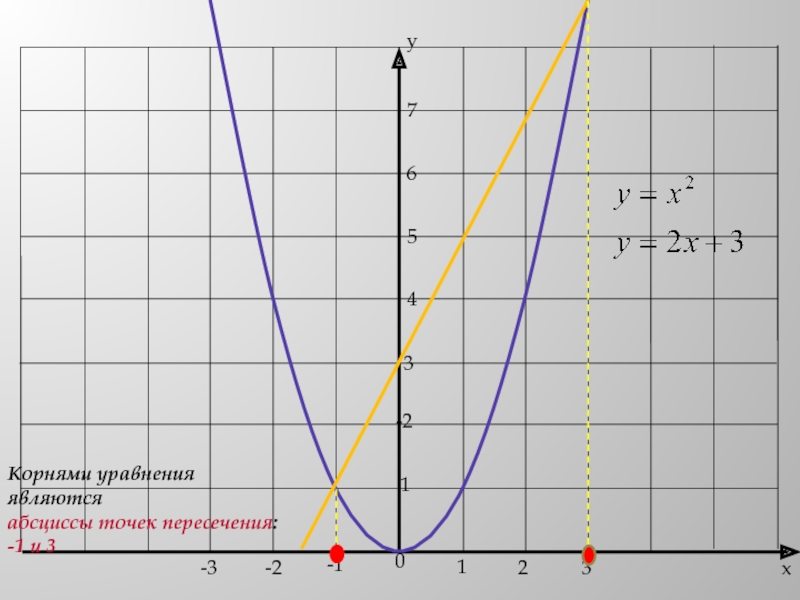
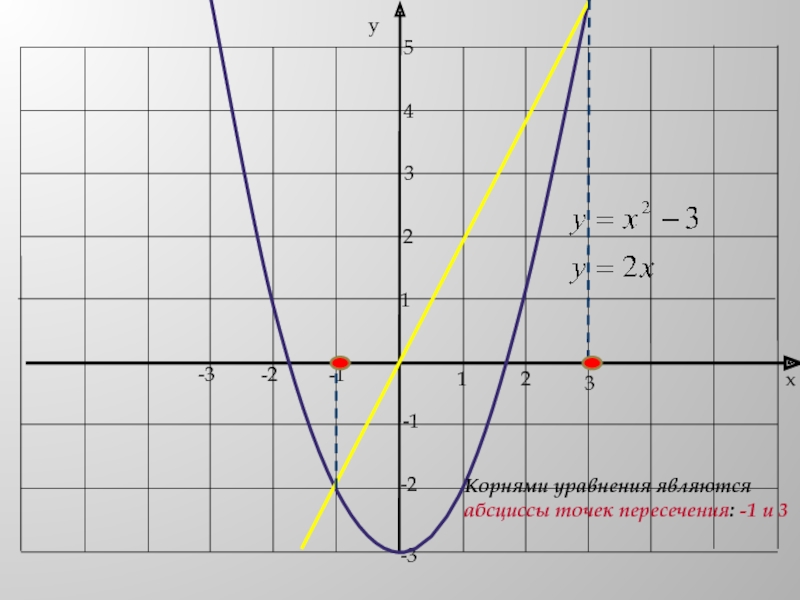
- 15. 3 способПреобразуем уравнение к видуПостроим в одной системе координат графики функций -парабола-прямая
- 16. -12-11ух321-23-3-2-354Корнями уравнения являются абсциссы точек пересечения: -1 и 3
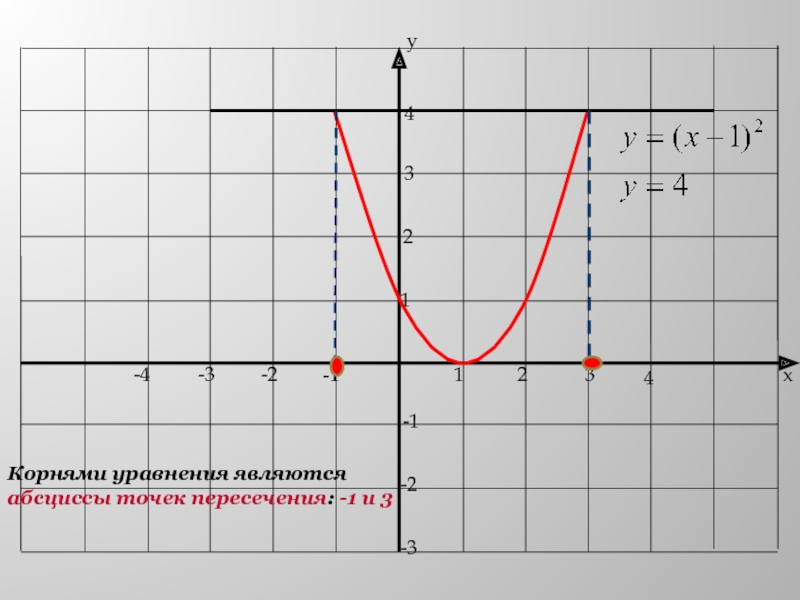
- 17. 4 способ Преобразуем уравнение к виду Построим в одной системе координат графики функций :, -парабола,-прямая.
- 18. -12-11ух321-23-3-2-344-4Корнями уравнения являются абсциссы точек пересечения: -1 и 3
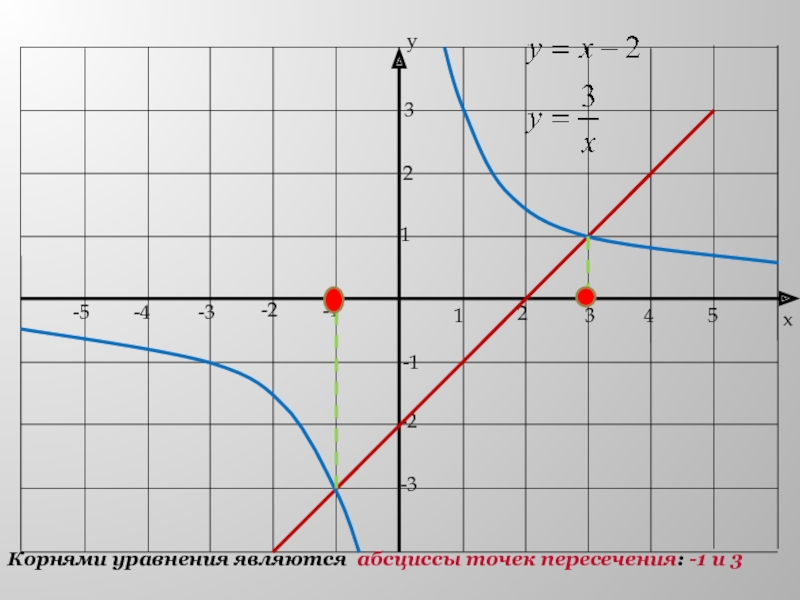
- 19. 5 способ Разделив почленно обе части уравнения на х, получим:Построим в одной системе координат :-гипербола,-прямая
- 20. Корнями уравнения являются абсциссы точек пересечения: -1 и 3
- 21. Первые четыре способа применимы к любым уравнениям
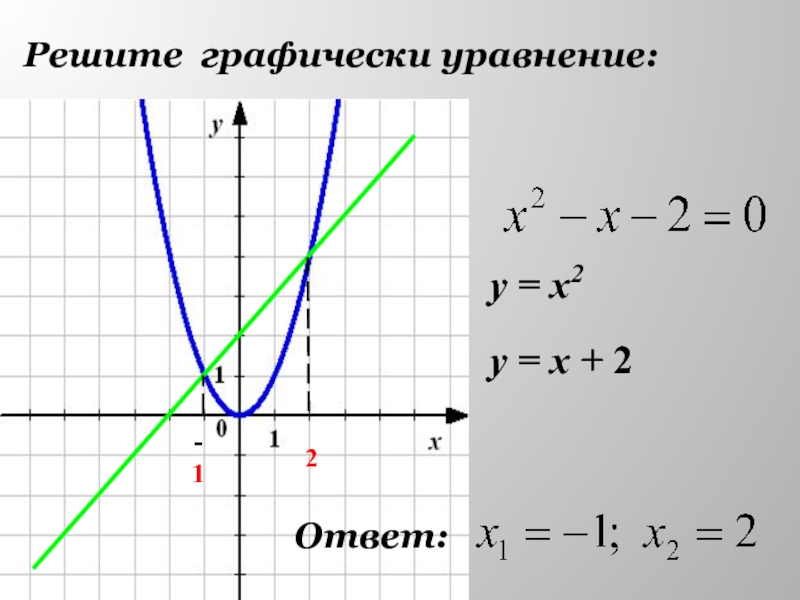
- 22. Решите графически уравнение:у = х2у = х + 2-12
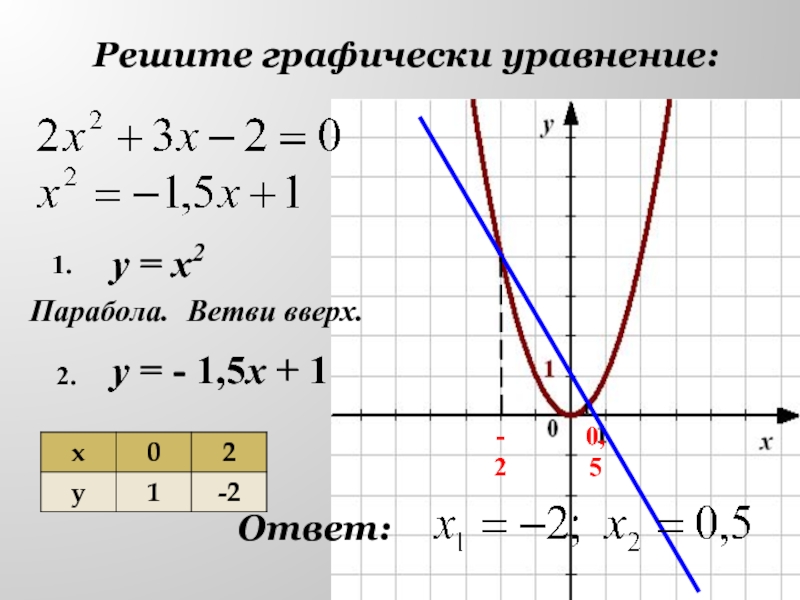
- 23. Решите графически уравнение:у = х2у = - 1,5х + 1Парабола.1.2.Ветви вверх.-20,5
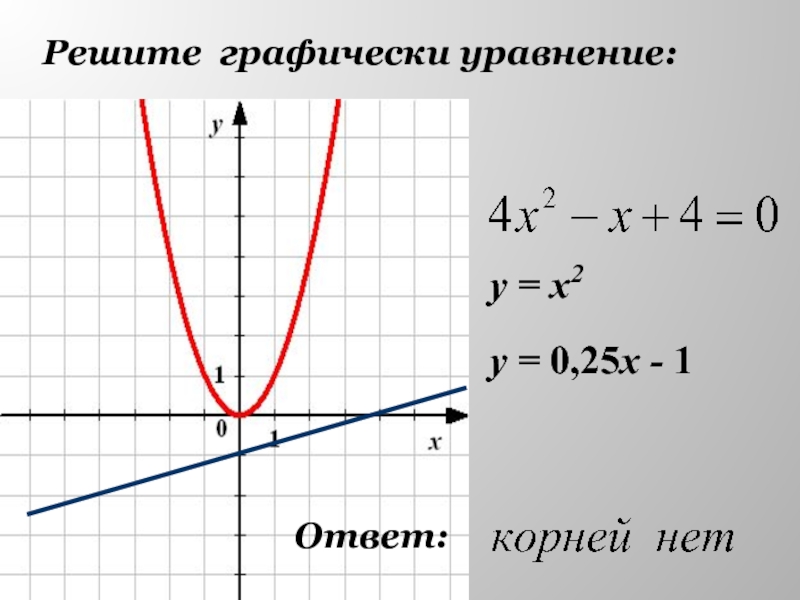
- 24. Решите графически уравнение:у = х2у = 0,25х - 1
- 25. Выберите способ и решите уравнение.Корней нетВывод: Графические
- 26. Решить в классе: №23.1(б),23.4(в),23.8(а).
- 27. Домашнее задание. п.23 читать,№23.4(а, б),23.1(а)
- 28. Скачать презентанцию
-12-11ух321-23-3-2-3
Слайды и текст этой презентации
Слайд 8Построить график функции
Найдём координаты вершины параболы
- ось симметрии параболы
- вершина
параболы
Слайд 10Определение
Квадратным уравнением называется уравнение вида
ах2 + bx + c=0
где х – переменная; а, b и с –
некоторые числа, причем а≠0 a, b и с – коэффициенты квадратного уравнения.
а - первый или старший коэффициент,
b – второй коэффициент или коэффициент,
с – свободный член.
Слайд 12Вершина параболы: (1; -4)
Корнями уравнения являются абсциссы точек пересечения с
осью х;
значит корни уравнения равны: -1 и 3
Слайд 13 2 способ
Преобразуем уравнение
к виду
Построим в одной системе координат графики функций :
- парабола
-прямая
Слайд 15 3 способ
Преобразуем уравнение
к виду
Построим в одной системе координат
графики функций
-парабола
-прямая
Слайд 174 способ
Преобразуем уравнение
к виду
Построим в одной системе координат
графики функций :
,
-парабола,
-прямая.
Слайд 195 способ
Разделив почленно обе части уравнения на х, получим:
Построим в
одной системе координат :
-гипербола,
-прямая
Слайд 21Первые четыре способа применимы к любым уравнениям вида
,а пятый –
только к тем, у которых с =0
Слайд 25Выберите способ и решите уравнение.
Корней нет
Вывод: Графические способы не дают
гарантии решения
любого квадратного уравнения .
Замечание страница 130.
