Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Графики функций у=ах2 +n, у=а(х-m)2
Содержание
- 1. Графики функций у=ах2 +n, у=а(х-m)2
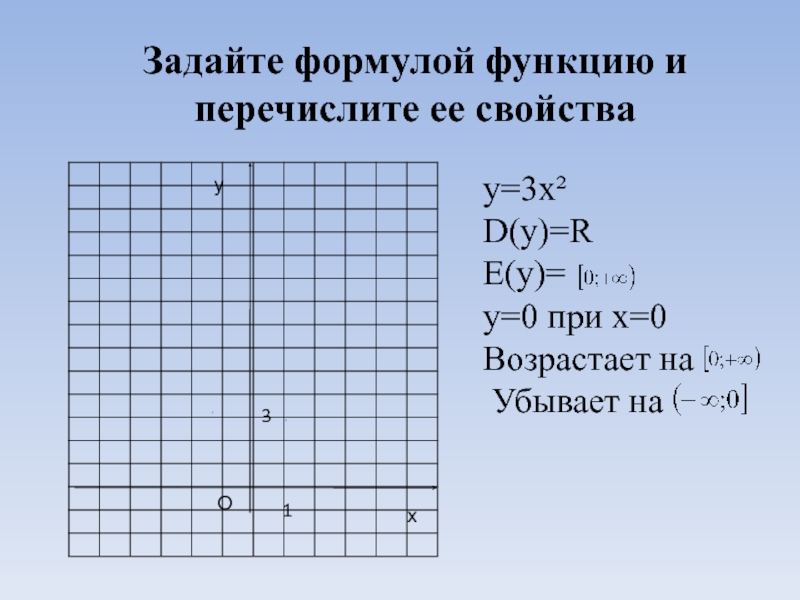
- 2. Задайте формулой функцию и перечислите ее свойствахуО31у=3х²D(y)=RE(y)=у=0 при х=0Возрастает на Убывает на
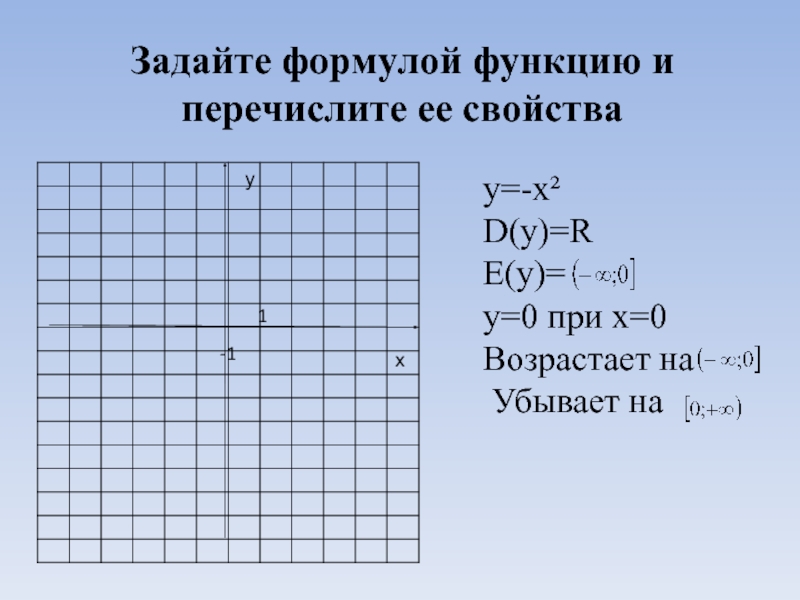
- 3. Задайте формулой функцию и перечислите ее свойстваух1-1у=-х²D(y)=RE(y)= у=0 при х=0Возрастает на Убывает на
- 4. Итоги прошлого урока:График функции у=-f(x) получается из
- 5. Сравним значения функций у=2х² и у=2х²+18202893139
- 6. Вершина параболы (0;1)Ось симметрии х=0ухО1
- 7. График функции у=f(x)+n можно получить из графика
- 8. Из графика функции у=х² получит графики функции:
- 9. Сравним значения функций у=2х² и у=2(х-1)²82028
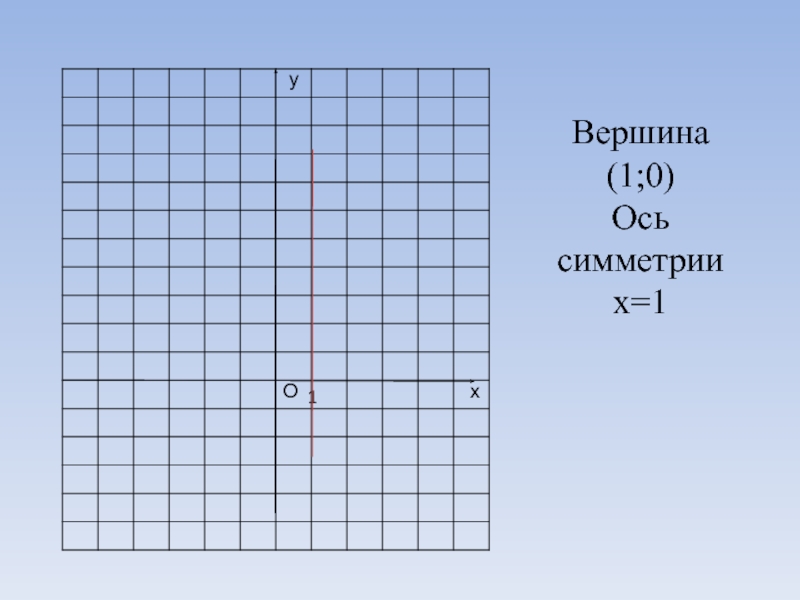
- 10. ухО1Вершина (1;0)Ось симметрии х=1
- 11. График функции у=f(x-m) получается из графика функции
- 12. Из графика функции у=х² построить графики функций:
- 13. График функции у=f(x-m)+n можно
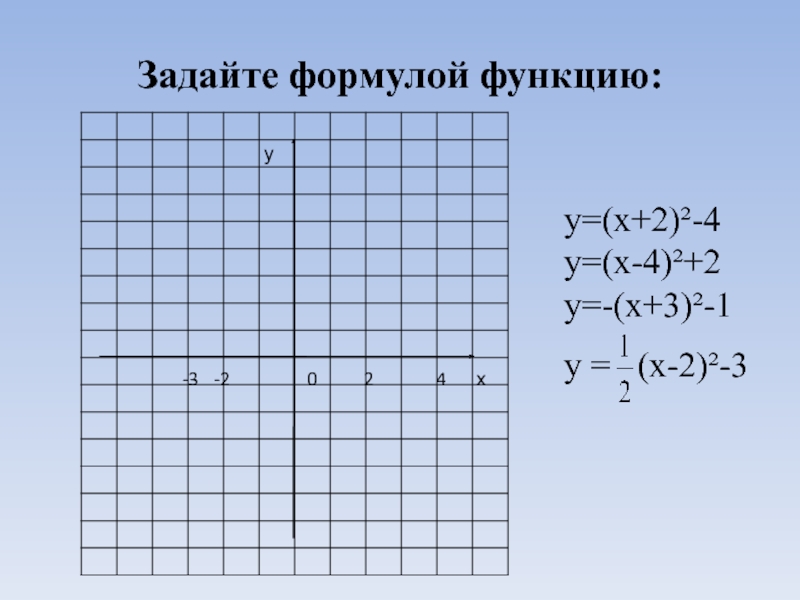
- 14. Задайте формулой функцию:у=(х+2)²-4у=(х-4)²+2у=-(х+3)²-1у = (х-2)²-3ух024-2-3
- 15. Скачать презентанцию
Задайте формулой функцию и перечислите ее свойствахуО31у=3х²D(y)=RE(y)=у=0 при х=0Возрастает на Убывает на
Слайды и текст этой презентации
Слайд 2Задайте формулой функцию и перечислите ее свойства
х
у
О
3
1
у=3х²
D(y)=R
E(y)=
у=0 при х=0
Возрастает на
Слайд 3Задайте формулой функцию и перечислите ее свойства
у
х
1
-1
у=-х²
D(y)=R
E(y)=
у=0 при х=0
Возрастает
на
Убывает на
Слайд 4Итоги прошлого урока:
График функции у=-f(x) получается из графика функции у=f(x)
с помощью симметрии относительно оси абсцисс.
2. График функции у=аf(x) получается
из графика функции у=f(x) растяжением вдоль оси ординат в а раз при а>1 и сжатием в раз при 0<а<1.
Слайд 7График функции у=f(x)+n можно получить из графика функции у=f(x) с
помощью параллельного переноса вдоль оси ординат на |n| единиц: вверх
при n>0 и вниз при n<0.
Слайд 8Из графика функции у=х² получит графики функции: а) у=х²+2
Б) у=х²-4 в) у=-х²+3 г) у=-х²-4
у
х
0
-4
2
3
Слайд 11График функции у=f(x-m) получается из графика функции у=f(x) с помощью
параллельного переноса вдоль оси абсцисс на |m| единиц: вправо, если
m>0 и влево, если m<0.
Слайд 12Из графика функции у=х² построить графики функций: а) у=(х-3)²
б) у=(х+2)² в) у=-(х-1)² г) у=-(х+1)²
у
х
0
-2
-1
3
1
Слайд 13 График функции у=f(x-m)+n можно получить из графика
функции у=f(x) с помощью двух параллельных переносов: сдвига вдоль оси
абсцисс на |m| единиц: вправо при m>0 и влево при m<0 и сдвига вдоль оси ординат на |n| единиц: вверх при n>0 и вниз при n<0.
