Интеграл и его практическое применение

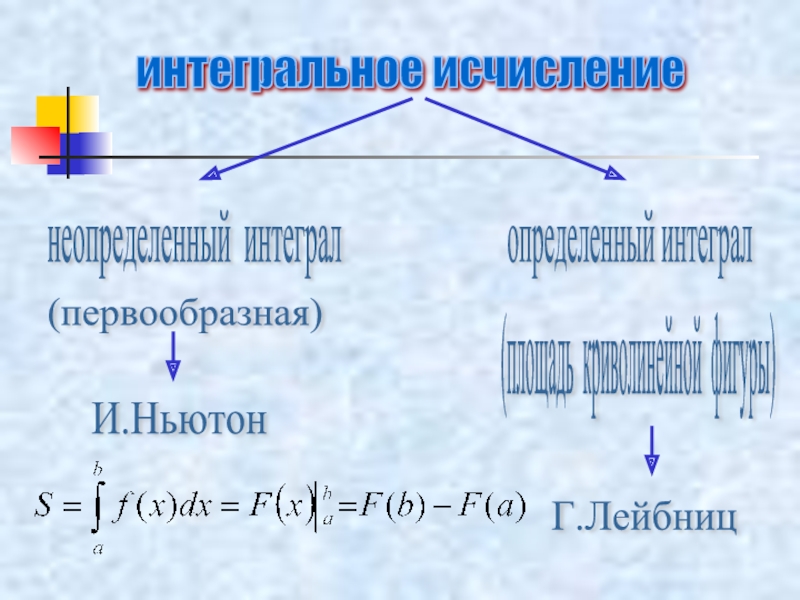
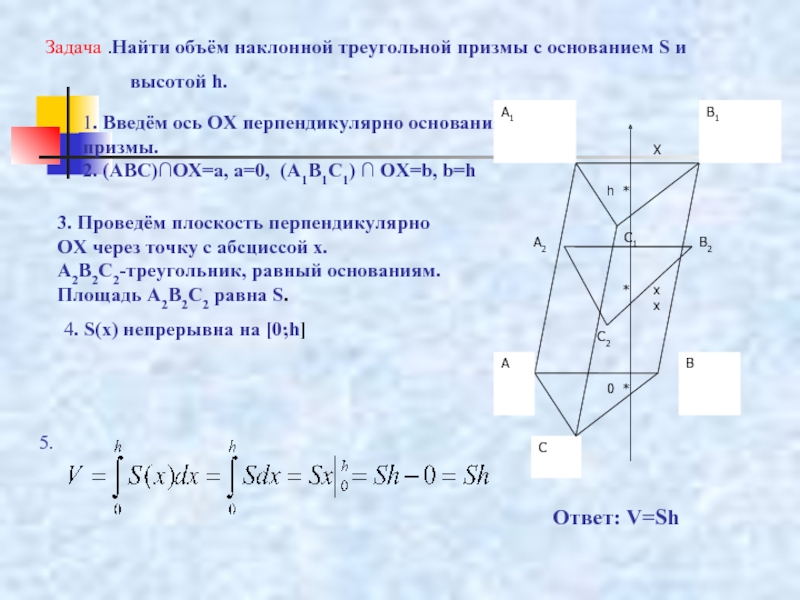
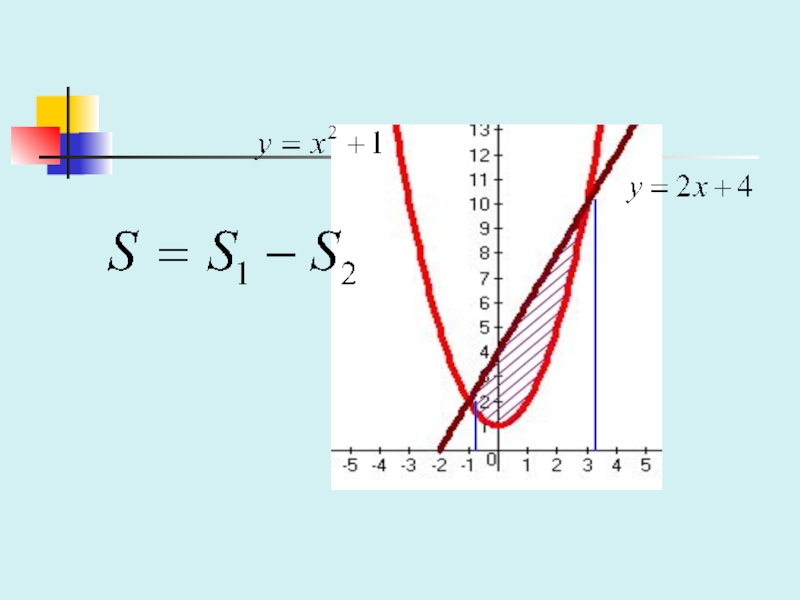
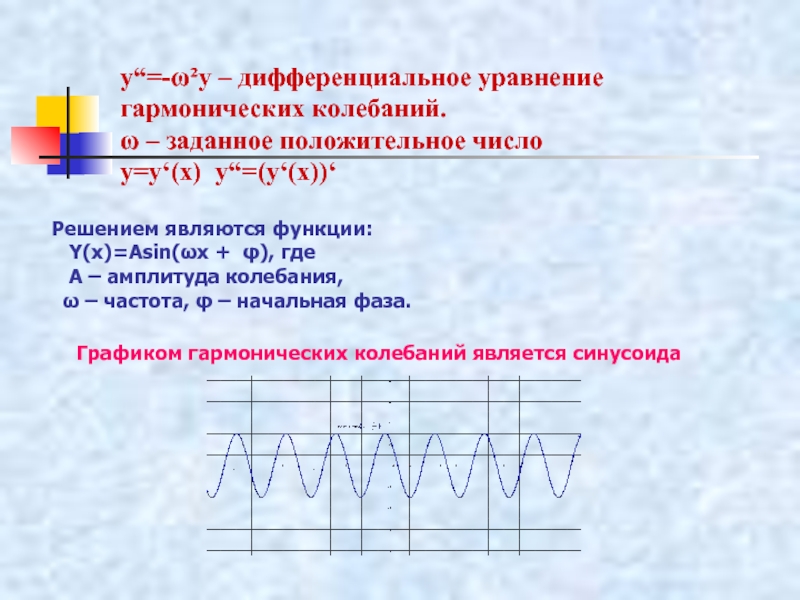
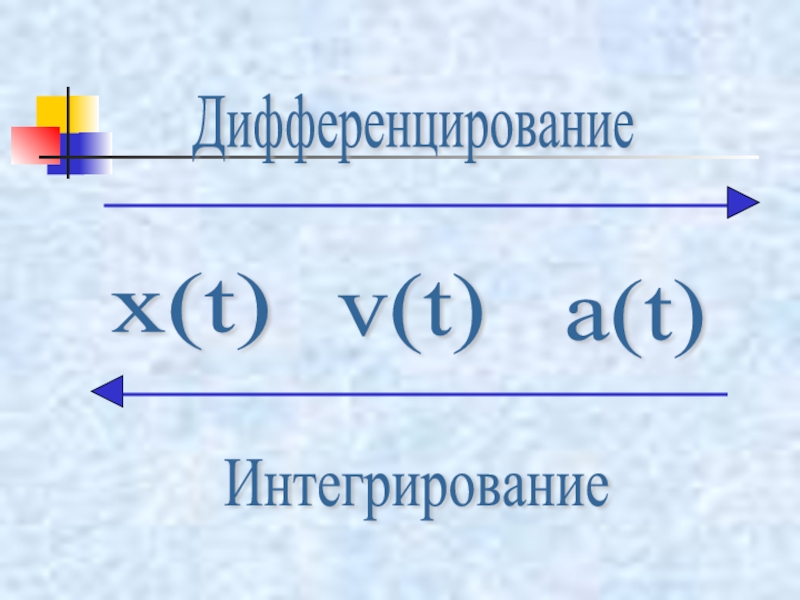практическое применение»
Сближение теории с практикой дает самые благоприятные результаты, и

не одна только практика от этого выигрывает, сами науки развиваются под влиянием ее.
П. Л. Чебышев

Большой Атлым
2012-2013 уч. год

Вывести общие формулы, позволяющие решать задачи интегрирования.
Показать, что интеграл

широко применяется в различных сферах жизнедеятельности.

рассмотреть, как интеграл используется при решении различных жизненных ситуаций;
-

использование интеграла в различных сферах жизнедеятельности.

Объект исследования:
область математики – интегрирование.

Ж Лагранж
5 век до н.э. др.гр. ученый Демокрит
3-4 век до

н.э. Архимед ввел метод исчерпывания

н.э.
Строгое изложение теории интегралов появилось только в 19 веке. Но

задачами на вычисление площадей занимались математики Древней Греции.

Математики Древней Греции

Лукреций

пособие, так как оно разгружает воображение… Следует заботиться о том,

чтобы обозначения были удобны для открытий. Обозначения коротко выражают и отображают сущность вещей. Тогда поразительным образом сокращается работа мысли.»
Лейбниц

И.Ньютон
Г.Лейбниц

Масса
Перемещение
Дифференциальное уравнение
Давление
Количество теплоты

высотой h.

1. Введём ось ОХ перпендикулярно основаниям призмы.
2. (АВС)∩OX=a, a=0, (A1B1C1) ∩ OX=b, b=h

3. Проведём плоскость перпендикулярно ОХ через точку с абсциссой х.
А2В2С2-треугольник, равный основаниям.
Площадь А2В2С2 равна S.

Ответ: V=Sh

4. S(x) непрерывна на [0;h]

количеству. За какое время количество бактерий увеличится в m раз

по сравнению с начальным?
Решение:
Пусть x(t) – количество бактерий в момент времени t. x(0) = x0. Изменение количества бактерий со временем описывается уравнением
x´(t) = kx(t), k>0, ,

ln|x| = kt+ln|C|,

x=ekteln|C| , x=Cekt - общее решение уравнения.

ЗАДАЧА

y“=(y‘(x))‘
Решением являются функции:
Y(x)=Asin(ωx + φ), где
A

– амплитуда колебания,
ω – частота, φ – начальная фаза.

Графиком гармонических колебаний является синусоида

в математике его времени не было понятия интеграла
Но лишь интегральное

исчисление дает общий метод решения задач из различных областей наук.
Недаром даже поэты воспевали интеграл.

Смысл- там, где змеи интеграла Меж цифр и букв , меж d и f. Там – власть, там творческие горны! Пред волей чисел все – рабы. И солнца путь вершат, покорны Немым речам и ворожбы. В.Брюсов. 

отработке техники интегрирования и изучении приложений способствует осознанному качественному усвоению

материала, развитию правильного представления об изучаемом понятии, его огромной значимости в различных науках, формированию мировоззрения, таких специальных качеств, как умение строить математические модели реальных процессов и явлений, исследовать и изучать их, а, следовательно, способствует развитию мышления, памяти, внимания и речи.