Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Степень с натуральным показателем
Содержание
- 1. Степень с натуральным показателем
- 2. Исторические сведенияДиофант Александрийский описывает первые натуральные степени
- 3. Нидерландский математик Симон Стевин (1548—1620). обозначал
- 4. Определение степени с натуральным показателемСтепенью числа а
- 5. Действия со степенямиУмножение степенейx2 ∙ x4 =
- 6. Деление степенейb6 : b2=(b ∙ b ∙
- 7. Возведение степени в степень(Y4)2=y4y4==y4+4 =y8(Y4)2=y4∙2=y8При возведении степени
- 8. Возведение в степень произведения(2xy)4=(2xy)∙(2xy)∙(2xy)∙(2xy)=24x4y4Степень произведения нескольких множителей
- 9. Возведение в степень дроби(3/х)5=(3/х)(3/х)(3/х)(3/х)(3/х)=35/х5При возведении дроби в
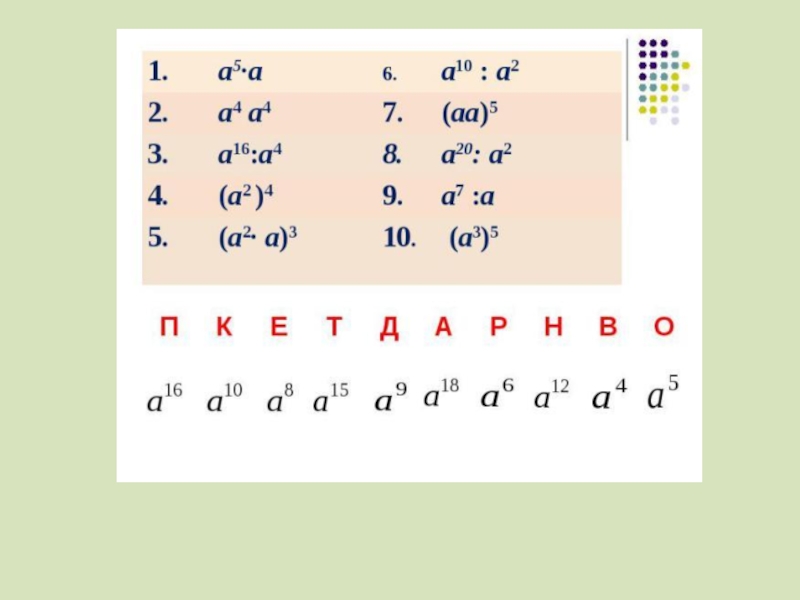
- 10. Проверь себяВместо звездочек * вставить такой показатель,
- 11. Слайд 11
- 12. Слайд 12
- 13. Рене Декарт (1596-1650)
- 14. Спасибо за внимание!
- 15. Скачать презентанцию
Исторические сведенияДиофант Александрийский описывает первые натуральные степени чисел так:«Все числа… состоят из некоторого количества единиц; ясно, что они продолжаются, увеличиваясь до бесконечности. …среди них находятся: квадраты, получающиеся от умножения некоторого числа
Слайды и текст этой презентации
Слайд 1Орехова Татьяна Константиновна
Учитель математики
ГБОУ ООШ №132 Калининский район
Степень с
натуральным показателем
Алгебра 7 класс
Слайд 2Исторические сведения
Диофант Александрийский описывает первые натуральные степени чисел так:
«Все числа…
состоят из некоторого количества единиц; ясно, что они продолжаются, увеличиваясь
до бесконечности. …среди них находятся: квадраты, получающиеся от умножения некоторого числа самого на себя; это же число называется стороной квадрата, затем кубы, получающиеся от умножения квадратов на их сторону, далее квадрато-квадраты — от умножения квадратов самих на себя, далее квадрато-кубы, получающиеся от умножения квадрата на куб его стороны, далее кубо-кубы — от умножения кубов самих на себя».
Слайд 3 Нидерландский математик Симон Стевин (1548—1620). обозначал неизвестную величину кружком
О, внутри которого указывал показатели степени. Стевин предложил называть степени
по их показателям - четвёртой, пятой и т.д. и отверг Диофантовы составные выражения «квадрато-квадрат», «квадрато-куб». Французский математик Рене Декарт в 1637 ввел современное обозначение степеней а?, а?,... Декарт считал, что а∙а не занимает больше места, чем а2 и не пользовался этим обозначением при записи произведения двух одинаковых множителей.
Слайд 4Определение степени с натуральным показателем
Степенью числа а с натуральным показателем
n называется произведение n множителей, каждый из которых равен а
аnа-основание степени
n- показатель степени
а∙а∙а∙а … а∙а∙а
n раз повторяющийся множитель
y ∙ y ∙ y ∙ y ∙ y=y5
(x-2)∙(x-2)∙(x-2)=(x-2)3
4/9 ∙ 4/9= (4/9)2
Слайд 5Действия со степенями
Умножение степеней
x2 ∙ x4 = x ∙ x
∙ x ∙ x ∙ x ∙ x=x6
x2 ∙ x4
= x2+4 = x6Произведение степеней с одинаковыми основаниями равно степени с этим же основанием и показателем, равным суммой показателей.
Свойства степеней с натуральным показателем
аn ∙аm = a n+m
Слайд 6Деление степеней
b6 : b2=
(b ∙ b ∙ b ∙ b
∙ b ∙ b):(b ∙ b)=
b ∙ b ∙ b
∙ b=b4b≠0
b6: b2=b6-
-2=b4
Частное степеней с одинаковыми основаниями равно степени с тем же основанием и показателем, равным разности показателей.
Чтобы разделить степень на степень с одинаковыми основаниями, надо основание оставить прежним и от показателя делимого вычесть показатель делителя.
Действия со степенями
am:an=am-n a≠0 m> n
Слайд 7Возведение степени в степень
(Y4)2=
y4y4==y4+
4 =y8
(Y4)2=y
4∙2
=y8
При возведении степени в степень основание
надо оставить прежним, а показатели перемножить.
Действия со степенями
(an)m=anm
Слайд 8Возведение в степень произведения
(2xy)4=(2xy)∙(2xy)∙(2xy)∙(2xy)=24x4y4
Степень произведения нескольких множителей равна произведению степеней
каждого множителя.
Чтобы возвести в степень несколько множителей, надо каждый множитель
возвести в заданную степень.Действия со степенями
(ab)n=an∙bn
Слайд 9Возведение в степень дроби
(3/х)5=(3/х)(3/х)(3/х)(3/х)(3/х)=
35/х5
При возведении дроби в степень числитель и
знаменатель возводится в заданную степень и записывается соответственно в числитель
и знаменатель дроби.Действия со степенями
(a/b)n =an/bn b≠0
Слайд 10Проверь себя
Вместо звездочек * вставить такой показатель, чтобы получилось верное
равенство
1. х3∙х* =х15
2. С*:С7=С3
3. (У7)*=У21
4. (6bc)*=64b4c4
5. (7/d)*=79/d9
12
10
3
4
9
