Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
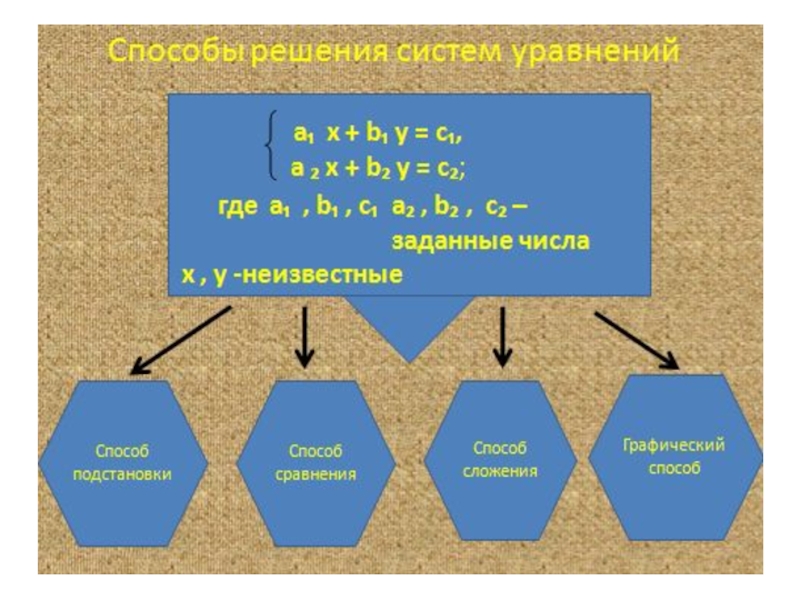
Графическое решение систем уравнений
Содержание
- 1. Графическое решение систем уравнений
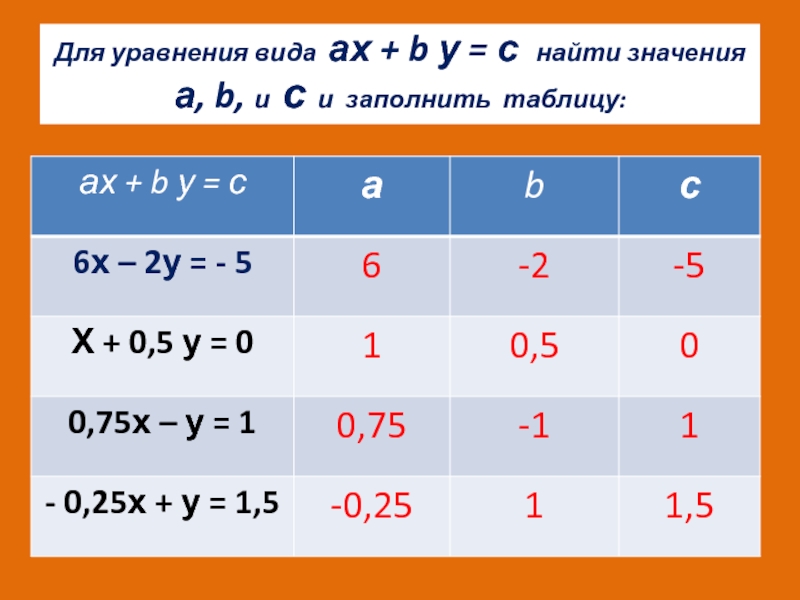
- 2. Для уравнения вида ах + b у
- 3. Для уравнения вида ах + b у
- 4. Графический способ
- 5. Из историиБлагодаря методу координат, созданному в 17
- 6. Графический способ (алгоритм)Выразить у через х в
- 7. Решение системы графическим способомy=10 - xy=x+2Выразим учерез хПостроим графикпервого уравненияу=х+2Построим графиквторого уравненияу=10 - хОтвет: (4; 6)
- 8. Три возможных случая взаимного расположения двух прямых
- 9. Задание1. Закончите предложение, чтобы получилось верное утверждениеВариант
- 10. Задание2. В каждом задании из трех предложенных
- 11. Задание 3. Показать, что система уравнений
- 12. Домашнее задание 1. Учебник «Алгебра 7»,
- 13. Спасибо всем за работу
- 14. Скачать презентанцию
Слайды и текст этой презентации
Слайд 4
Графический способ
Цель:
научить графическому способу
решения систем линейных уравнений с двумя неизвестными.
Слайд 5Из истории
Благодаря методу координат, созданному в 17 веке Ферма и
Декартом, стало возможным геометрическое решение уравнений систем. Так называемый графический
метод решения состоит в построении абсциссы х и ординаты у точки пересечения двух соответствующих прямых.Из истории
а₁ х + b ₁ y= c₁
a₂ х + b₂ y = c₂
у
х
Слайд 6Графический способ (алгоритм)
Выразить у через х в каждом уравнении
Построить в
одной системе координат график каждого уравнения
Определить координаты точки пересечения
Записать ответ:
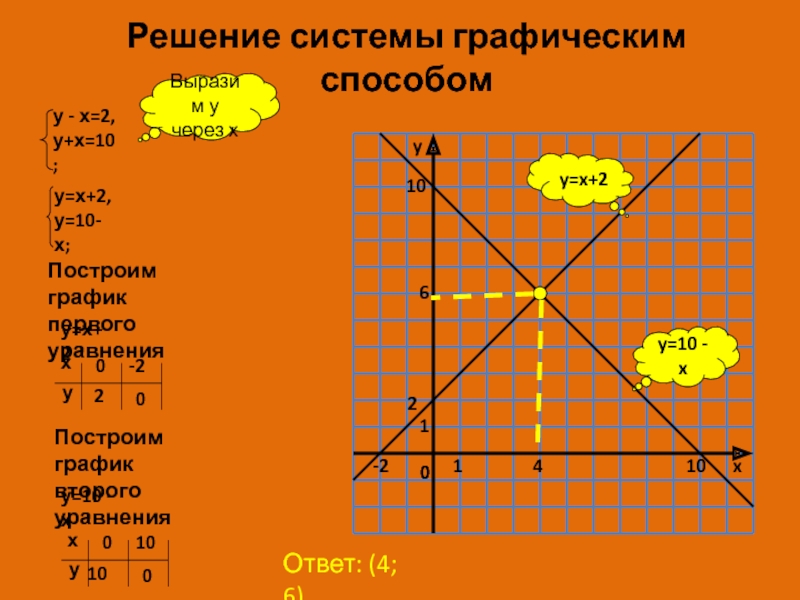
х ≈…; у ≈… , или (х; у) Слайд 7Решение системы графическим способом
y=10 - x
y=x+2
Выразим у
через х
Построим график
первого уравнения
у=х+2
Построим
график
второго уравнения
у=10 - х
Ответ: (4; 6)
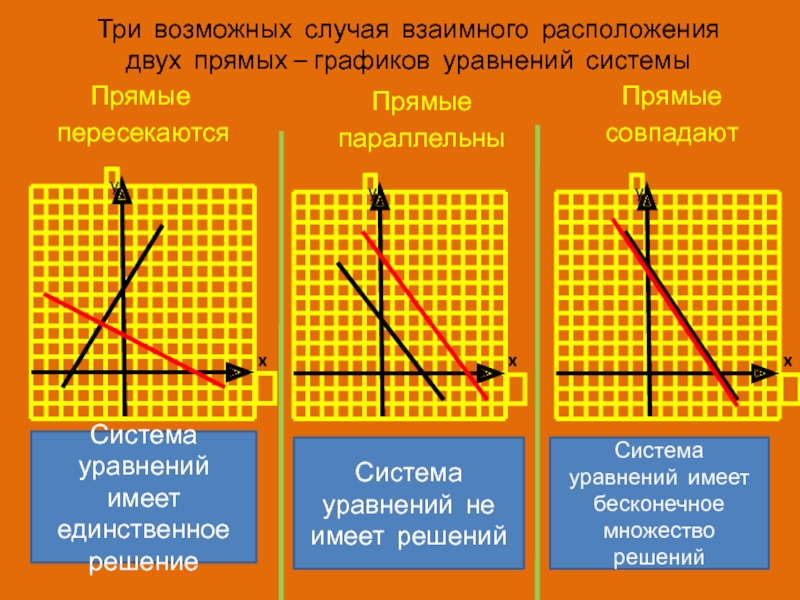
Слайд 8Три возможных случая взаимного расположения двух прямых – графиков уравнений
системы
Прямые
параллельны
Прямые
пересекаются
Прямые
совпадают
Система уравнений имеет единственное решение
Система уравнений не
имеет решенийСистема уравнений имеет бесконечное множество решений
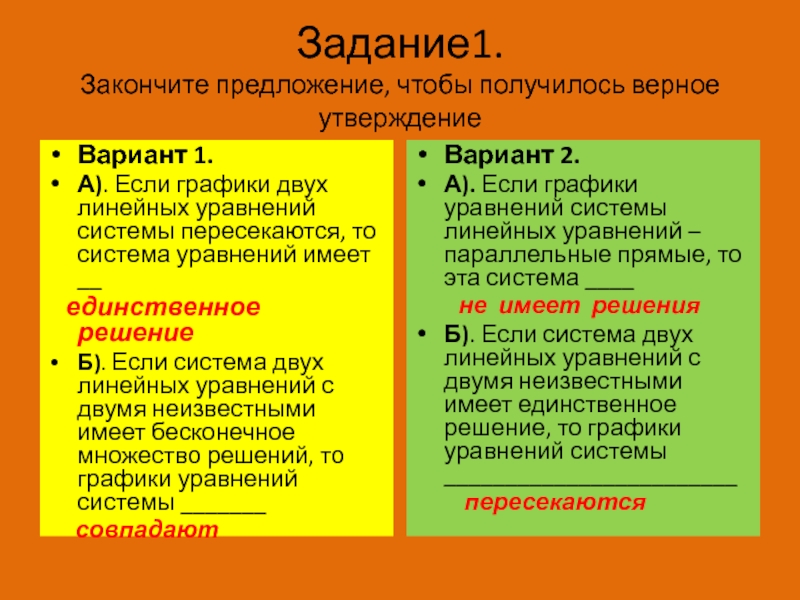
Слайд 9Задание1.
Закончите предложение, чтобы получилось верное утверждение
Вариант 1.
А). Если графики двух
линейных уравнений системы пересекаются, то система уравнений имеет __
единственное решениеБ). Если система двух линейных уравнений с двумя неизвестными имеет бесконечное множество решений, то графики уравнений системы _______
совпадают
Вариант 2.
А). Если графики уравнений системы линейных уравнений – параллельные прямые, то эта система ____
не имеет решения
Б). Если система двух линейных уравнений с двумя неизвестными имеет единственное решение, то графики уравнений системы ________________________
пересекаются
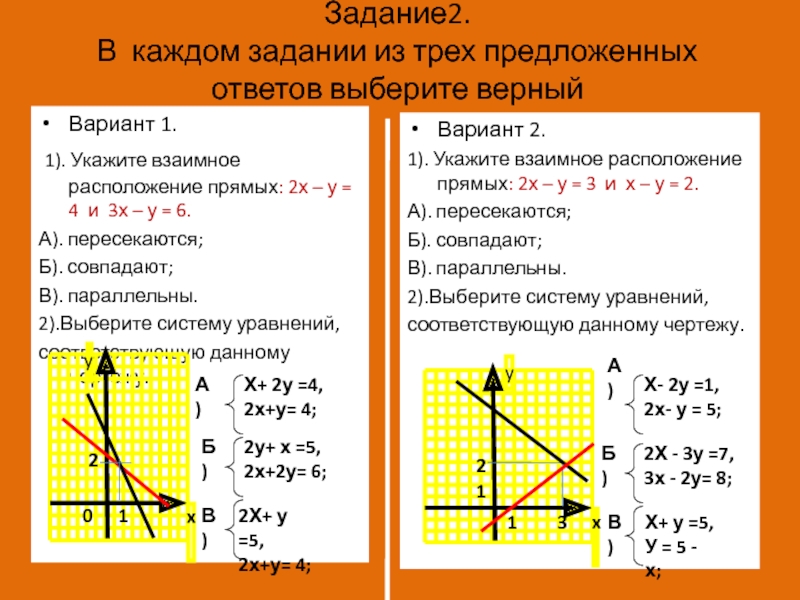
Слайд 10Задание2.
В каждом задании из трех предложенных ответов выберите верный
Вариант 1.
1). Укажите взаимное расположение прямых: 2х – у = 4
и 3х – у = 6.А). пересекаются;
Б). совпадают;
В). параллельны.
2).Выберите систему уравнений,
соответствующую данному чертежу.
Вариант 2.
1). Укажите взаимное расположение прямых: 2х – у = 3 и х – у = 2.
А). пересекаются;
Б). совпадают;
В). параллельны.
2).Выберите систему уравнений,
соответствующую данному чертежу.
0
1
2
Б)
В)
А)
Б)
А)
В)
1
3
1
2
Слайд 11 Задание 3. Показать, что система уравнений бесконечно много решений. Что это означает
геометрически ?
Решение.
1. Разделив обе части первого уравнения на
2 иобе части второго уравнения на 3, получим
систему …………………
· 2. Уравнения системы оказались ………… это
означает, что система ……. Геометрически это
означает, что графиками этих уравнений
являются………….
Слайд 12Домашнее задание
1. Учебник «Алгебра 7»,
авторы Ш.А.Алимов и др. § 36
№ 644(2), 645(4), 648(2).2. Рабочая тетрадь по алгебре, 7,
авторы Ю.М.Колягин и др.
§ 36, № (9).
3. Дополнительно: Дидактические материалы
«Алгебра 7», авторы М.В.Ткачева и др.
§ 36 ( стр. 94) № 5(2).