Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Исходные понятия теории множеств 11 класс
Содержание
- 1. Исходные понятия теории множеств 11 класс
- 2. Содержание Понятие множества.Конечные, бесконечные множества.Способы задания множеств.Операции над множествами.Диаграммы Эйлера-Венна.Примеры для закрепления.
- 3. Дискретная математика — часть математики, изучающая дискретные — часть
- 4. Понятие множества является одним из наиболее общих
- 5. Множества обычно обозначаются заглавными латинскими буквами. Если
- 6. Пустое множествоСреди множеств выделяют особое множество -
- 7. Пустое множество является частью любого множества. Это
- 8. Определенные, конечные, бесконечные множестваМножество считается определенным, если
- 9. Пример Множество натуральных чисел является бесконечным. Упорядоченное
- 10. Способы задания множествПример: Множество учеников данного класса
- 11. Множества А и В равны, если они
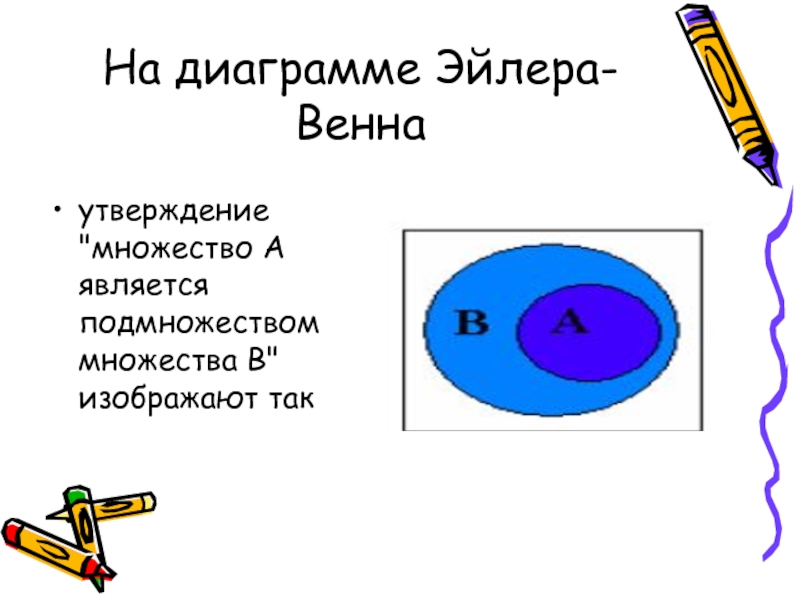
- 12. На диаграмме Эйлера-Веннаутверждение "множество А является подмножеством множества В" изображают так
- 13. Основные теоретико-множественные операции 1. Объединение2. Пересечение3. Разность4. Дополнение.
- 14. Объединение Объединением двух множеств называется новое
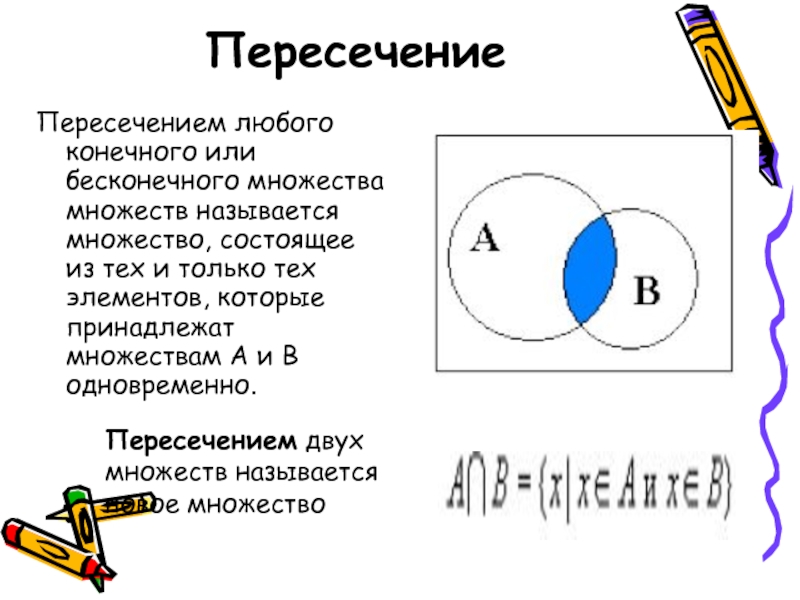
- 15. ПересечениеПересечением любого конечного или бесконечного множества множеств
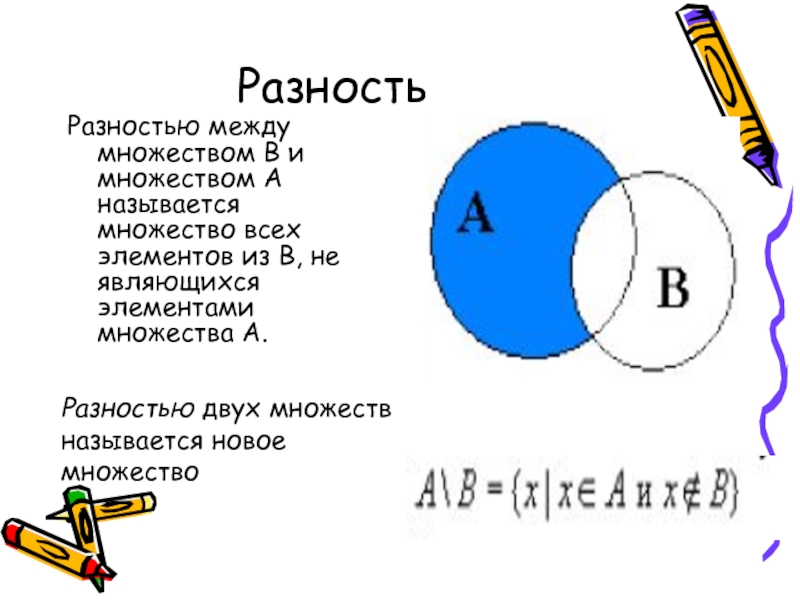
- 16. РазностьРазностью между множеством В и множеством А
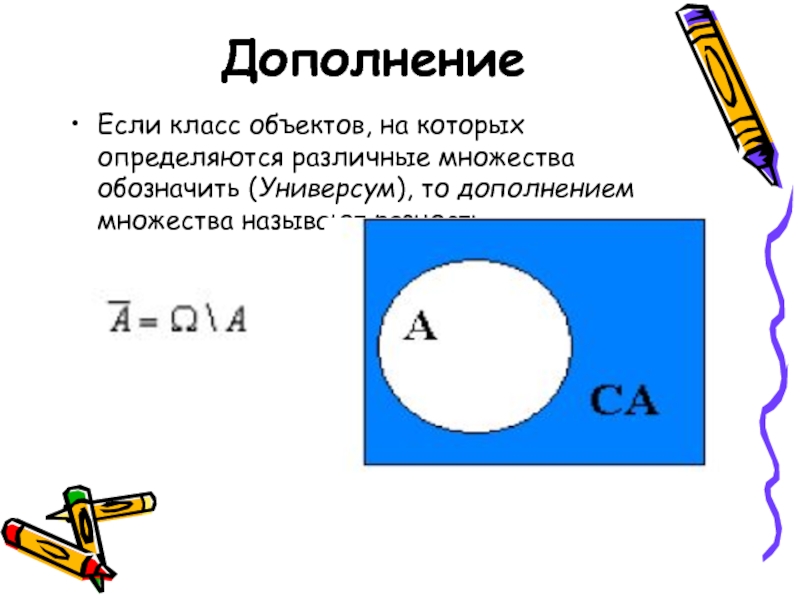
- 17. ДополнениеЕсли класс объектов, на которых определяются различные множества обозначить (Универсум), то дополнением множества называют разность
- 18. Примеры для закрепления
- 19. Слайд 19
- 20. Слайд 20
- 21. Слайд 21
- 22. Слайд 22
- 23. Слайд 23
- 24. Слайд 24
- 25. ЛитератураГладков, Л.А. Дискретная математика / Л.А. Гладков,
- 26. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1
Исходные понятия теории множеств
ГБПОУ Уфимский многопрофильный профессиональный колледж
Преподаватель математики
Сагадатова Гульназ
Фармутовна
Слайд 2Содержание
Понятие множества.
Конечные, бесконечные множества.
Способы задания множеств.
Операции над множествами.
Диаграммы Эйлера-Венна.
Примеры
для закрепления.
Слайд 3Дискретная математика — часть математики, изучающая дискретные — часть математики, изучающая дискретные
математические структуры — часть математики, изучающая дискретные математические структуры, такие, как
графы — часть математики, изучающая дискретные математические структуры, такие, как графы и утверждения в логике.В контексте математики в целом дискретная математика часто отождествляется с конечной математикой — направлением, изучающим конечные структуры — конечные графы — направлением, изучающим конечные структуры — конечные графы, конечные группы — направлением, изучающим конечные структуры — конечные графы, конечные группы, конечные автоматы
Слайд 4Понятие множества является одним из наиболее общих и наиболее важных
математических понятий. Оно было введено в математику немецким ученым Георгом
Кантором (1845-1918). Следуя Кантору, понятие «множество» можно определить так:Множество - совокупность объектов, обладающих определенным свойством, объединенных в единое целое. Объекты, составляющие множество, называются элементами множества.
Слайд 5Множества обычно обозначаются заглавными латинскими буквами.
Если элемент x принадлежит
множеству A, то это обозначается:
х∈А
Если каждый элемент множества B является также и элементом множества A, то говорят, что множество B является подмножеством множества A или включается в него: B⊂A.
Например, множество всех четных чисел является подмножеством множества всех целых чисел, а множество {0,1,2} – подмножеством множества {0,1,2,3}.
Слайд 6Пустое множество
Среди множеств выделяют особое множество - пустое множество. Пустое
множество- множество, не содержащее ни одного элемента.
Необходимость рассмотрения пустого множества
видна из того, что когда мы определяем тем или иным способом множество, то мы можем и не знать заранее, содержит ли оно хотя бы один элемент.Например, вероятно, множество страусов, находящихся в данный момент за Полярным кругом, пусто; однако мы не можем этого утверждать с уверенностью, т.к. может быть какой-нибудь капитан и завез какого-нибудь страуса за Полярный круг.
Слайд 7Пустое множество является частью любого множества.
Это множество настолько важное,
что для него даже придумали особый символ: ∅
Символ для
пустого множества только один, потому что пустое множество единственно. В самом деле, предположим, что существуют два разных пустых множества. Но что значит, что множества разные? Это значит, что в одном из них найдется элемент, который не принадлежит другому. Но в пустых множествах вообще элементов нет!
Слайд 8Определенные, конечные, бесконечные множества
Множество считается определенным, если указаны все его
элементы.
Конечное множество - множество, состоящее из конечного числа элементов.
Основной
характеристикой конечного множества является число его элементов. Теория конечных множеств изучает правила: как, зная количество элементов некоторых множеств, вычислить количество элементов других множеств, которые составлены из первых с помощью некоторых операций.Бесконечное множество - непустое множество, не являющееся конечным.
Слайд 9Пример
Множество натуральных чисел является бесконечным.
Упорядоченное множество - множество,
каждому элементу которого поставлено в соответствие некоторое число (номер этого
элемента) от 1 до n, где n - число элементов множества, так что различным элементам соответствуют различные числа.Каждое конечное множество можно сделать упорядоченным, если, например, переписать все элементы в некоторый список (a, b, c, d,...), а затем поставить в соответствие каждому элементу номер места, на котором он стоит в списке.
Слайд 10Способы задания множеств
Пример: Множество учеников данного класса определяется их списком
в классном журнале.
Пример: Хотя множество всех рыб в океане конечно,
вряд ли его можно задать списком.В тех случаях, когда множество нельзя задать при помощи списка, его задают путем указания некоторого характеристического свойства. Свойство является характеристическим для некоторого множества, если этому множеству принадлежат в точности те элементы, которые обладают данным свойством.
Пример: Свойство "быть квадратом целого числа" задает (бесконечное) множество всех квадратов целых чисел.
Слайд 11Множества А и В равны, если они состоят из одних
и тех же элементов.
Равенство множеств А и В записывают в
виде А=В. Отношение "=" называется отношением равенства.Множество А называют подмножеством множества В, если каждый элемент множества А является в то же время элементом множества В.
То, что множество А является подмножеством множества В обозначают так А⊂В
Данное отношение называется отношением включения.
Таким образом, подмножеством данного множества В является и само множество В.
Пустое множество, по определению, считают подмножеством всякого множества.
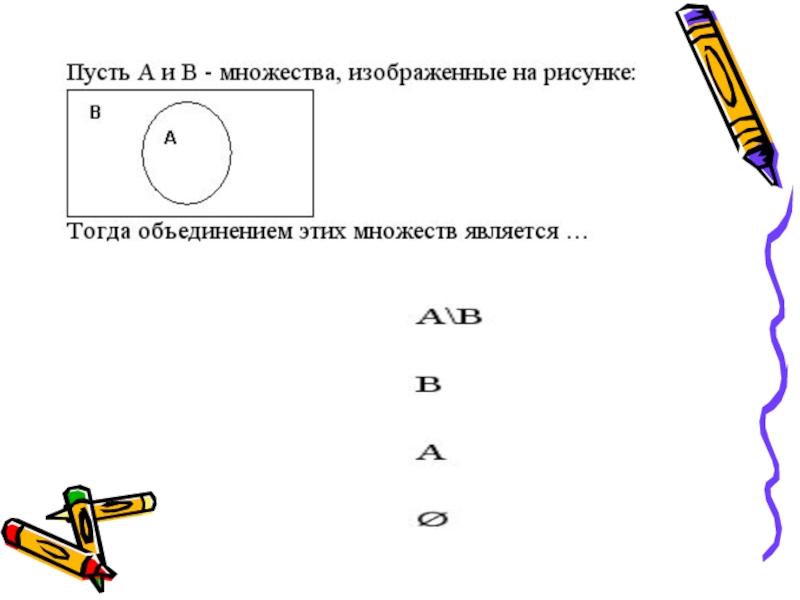
Слайд 12На диаграмме Эйлера-Венна
утверждение "множество А является подмножеством множества В" изображают
так
Слайд 13Основные теоретико-множественные операции
1. Объединение
2. Пересечение
3. Разность
4. Дополнение.
Слайд 14
Объединение
Объединением двух множеств называется новое множество
Суммой, или объединением произвольного конечного
или бесконечного множества
множеств называется множество, состоящее из тех и только
тех элементов, которые принадлежат хотя бы одному из множеств А, В.Слайд 15Пересечение
Пересечением любого конечного или бесконечного множества множеств называется множество, состоящее
из тех и только тех элементов, которые принадлежат множествам А
и В одновременно.Пересечением двух множеств называется новое множество