Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Вероятность. Правила сложения и умножения вероятностей
Содержание
- 1. Вероятность. Правила сложения и умножения вероятностей
- 2. Задачи по теории вероятностей и комбинаторике про шары
- 3. Ожидаемые результаты урокаСОТ 10.2. понимать и применять
- 4. № 1. В корзине содержится 6 черных и
- 5. № 1. В корзине содержится 6 черных и
- 6. № 2. Из корзины содержащей, 6 белых шаров,
- 7. № 2. Из корзины содержащей, 6 белых шаров,
- 8. № 3. В корзине 5 белых и 4
- 9. № 3. В корзине 5 белых и 4
- 10. № 3. В корзине 2 белых и 8 черных шаров. Из
- 11. № 3. В урне 2 белых и 8 черных шаров. Из
- 12. №4. Имеются три одинаковые урны. В первой
- 13. №4. Имеются три одинаковые урны. В первой
- 14. №5. В первой урне находится 6 белых
- 15. №6. Из урны, содержащей 5 шаров с
- 16. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Раздел 10.4.B
Правила сложения и умножения вероятностей
Назарбаев Интеллектуальная школа химико –биологического
направления
Слайд 3Ожидаемые результаты урока
СОТ 10.2. понимать и применять правила сложения и
умножения вероятностей.
* P(A ∩ B) = P(A) × P(B)
*
P(A U B) = P(A) + P(B)* P(A U B) = P(A) + P(B) – P(A ∩ B)
Слайд 4№ 1. В корзине содержится 6 черных и 5 белых шаров.
Случайным образом вынимают 5 шаров. Найти вероятность того, что среди них
имеется 3 белых шара.Слайд 5№ 1. В корзине содержится 6 черных и 5 белых шаров.
Случайным образом вынимают 5 шаров. Найти вероятность того, что среди них
имеется 3 белых шара.1
Решение. Перенумеруем все шары. Всего шаров 11. Исходом считаем выбор 5 любых шаров.
11
Количество всех исходов равно С115 = 11!/(5!6!) = 11*10*9*8*7/(2*3*4*5) = 462.
Благоприятный исход - выбор 3 белых шаров и двух черных.
3 шара из 5 можно выбрать С53 способами.
А выбрать 2 черных шара из 6 можно С62 способами.
Количество благоприятных исходов равно произведению
С53 * С62 = 5!/(3!*2!) * 6!/(2!*4!) = 5*4*3*2/(3*2*2) * 6*5*4*3*2/(2*4*3*2) = 10 * 15 = 150
Р = 150 / 462 ≈ 0,325
Слайд 6№ 2. Из корзины содержащей, 6 белых шаров, 5 черных и
3 красных, достают наугад 4 шара. Найти вероятность, что среди
вынутых шаров есть хотя бы по одному шару каждого цвета.Слайд 7№ 2. Из корзины содержащей, 6 белых шаров, 5 черных и
3 красных, достают наугад 4 шара. Найти вероятность, что среди
вынутых шаров есть хотя бы по одному шару каждого цвета.Решение. Задачу можно переформулировать так: найти вероятность того, что вынуты три шара разного цвета (четвертый может быть любым).
Всего шаров 6+5+3=14. Исход - выбор трех шаров из 14.
Всего исходов: С143= 14!/(3!*11!) = 14*13*12/(2*3) = 364
Благоприятный исход - выбраны 3 разных по цвету шара, а четвертый шар - любого цвета из оставшихся 11 шаров.
Количество благоприятных исходов равно С61*С51*С31 =6*5*3=90
Р=90/364 = 0,247
Слайд 8№ 3. В корзине 5 белых и 4 черных шара. Из
урны наугад вынимают два шара. Какова вероятность того, что это
будет: а) два белых шара; б) два черных шара; в) один черный и один белый.Слайд 9№ 3. В корзине 5 белых и 4 черных шара. Из
урны наугад вынимают два шара. Какова вероятность того, что это
будет: а) два белых шара; б) два черных шара; в) один черный и один белый.Решение.
a) Вероятность, что первый шар белый Р=5/9
Осталось 4 белых, всего 8 шаров, вероятность вытащить второй белый = 4/8=1/2
Р=5/9*1/2 = 5/18 =0,28
б) Р=4/9 * 3/8 = 1/6
в) Вероятность, что первый черный, а второй белый Р=4/9 * 5/8 = 5/18
Вероятность, что первый белый, а второй черный Р=5/9 * 4/8 = 5/18
Окончательно, вероятность, что 1 белый и один черный Р=5/18 + 5/18 = 10/18 = 5/9
Слайд 10№ 3. В корзине 2 белых и 8 черных шаров. Из урны извлекают 2
шара. Какова вероятность того, а)что эти шары черного цвета? б)одинаковые? в)
разных цветов?Слайд 11№ 3. В урне 2 белых и 8 черных шаров. Из урны извлекают 2
шара. Какова вероятность того, 1)что эти шары черного цвета? 2)одинаковые? 3)
разных цветов?Решение. Всего шаров в первой урне 10.
1) Вероятность извлечь первым черный шар из первой урны равна 8/10, останется 9 шаров, из них 7 черных. Вероятность извлечь черны шар равна 7/9.
Вероятность того, что первый черный и второй черный Р1=8/10*7/9= 28/45 = 0,6222..≈ 0,62
2) Аналогично находим, что оба шара белые.
Р2 = 2/10 * 1/9 = 1/45 ≈ 0,02
Вероятность, что оба шара одного цвета (или оба черные или оба белые) равна
Р = Р1+Р2 = 28/45+1/45 = 29/45 = 0,64
3) Вероятность, что первый белый, а второй черный Р3= 2/10 * 8/9 = 8/45
Вероятность, что первый черный, а второй белый Р4 = 8/10 * 2/9 = 8/45
Р = Р3+Р4 = 16/45 = 0,35
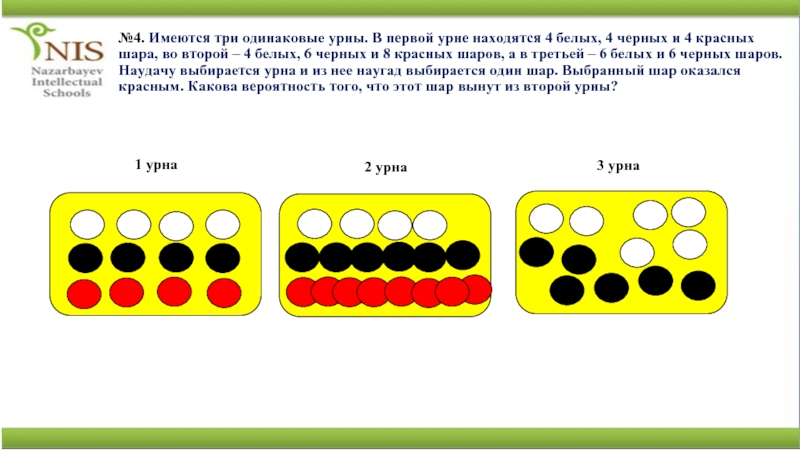
Слайд 12№4. Имеются три одинаковые урны. В первой урне находятся 4
белых, 4 черных и 4 красных шара, во второй –
4 белых, 6 черных и 8 красных шаров, а в третьей – 6 белых и 6 черных шаров. Наудачу выбирается урна и из нее наугад выбирается один шар. Выбранный шар оказался красным. Какова вероятность того, что этот шар вынут из второй урны?1 урна
2 урна
3 урна
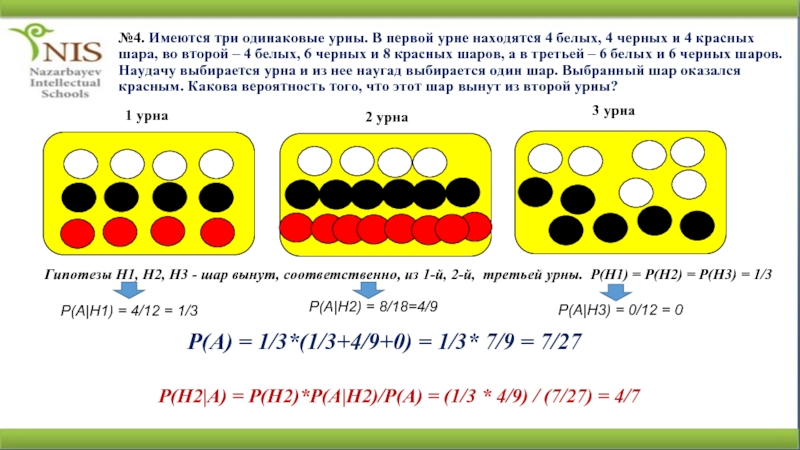
Слайд 13№4. Имеются три одинаковые урны. В первой урне находятся 4
белых, 4 черных и 4 красных шара, во второй –
4 белых, 6 черных и 8 красных шаров, а в третьей – 6 белых и 6 черных шаров. Наудачу выбирается урна и из нее наугад выбирается один шар. Выбранный шар оказался красным. Какова вероятность того, что этот шар вынут из второй урны?1 урна
2 урна
3 урна
Гипотезы Н1, Н2, Н3 - шар вынут, соответственно, из 1-й, 2-й, третьей урны. Р(Н1) = Р(Н2) = Р(Н3) = 1/3
P(A|H1) = 4/12 = 1/3
P(A|H2) = 8/18=4/9
P(A|H3) = 0/12 = 0
P(A) = 1/3*(1/3+4/9+0) = 1/3* 7/9 = 7/27
P(H2|A) = P(H2)*P(A|H2)/P(A) = (1/3 * 4/9) / (7/27) = 4/7
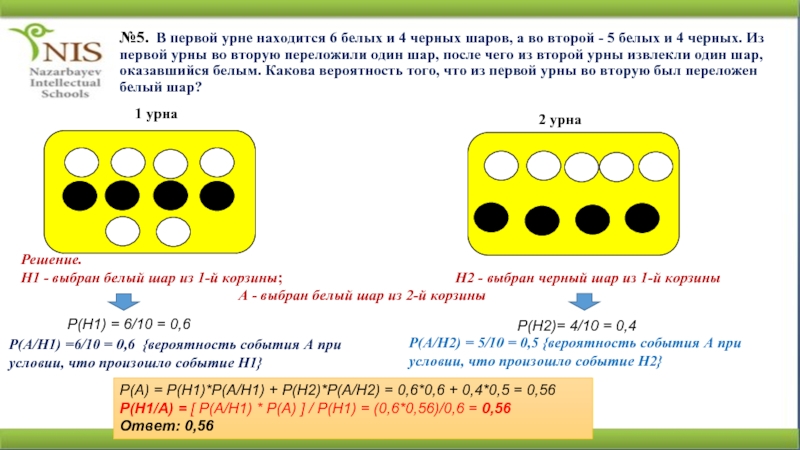
Слайд 14№5. В первой урне находится 6 белых и 4 черных
шаров, а во второй - 5 белых и 4 черных.
Из первой урны во вторую переложили один шар, после чего из второй урны извлекли один шар, оказавшийся белым. Какова вероятность того, что из первой урны во вторую был переложен белый шар?1 урна
2 урна
Решение.
Н1 - выбран белый шар из 1-й корзины; Н2 - выбран черный шар из 1-й корзины
А - выбран белый шар из 2-й корзины
Р(Н1) = 6/10 = 0,6
Р(Н2)= 4/10 = 0,4
Р(А/Н1) =6/10 = 0,6 {вероятность события А при условии, что произошло событие Н1}
Р(А/Н2) = 5/10 = 0,5 {вероятность события А при условии, что произошло событие Н2}
Р(А) = Р(Н1)*Р(А/Н1) + Р(Н2)*Р(А/Н2) = 0,6*0,6 + 0,4*0,5 = 0,56
Р(Н1/А) = [ Р(А/Н1) * Р(А) ] / Р(Н1) = (0,6*0,56)/0,6 = 0,56
Ответ: 0,56
Слайд 15№6. Из урны, содержащей 5 шаров с номерами от 1
до 5, последовательно извлекаются два шара, причем первый шар возвращается,
если номер не равен единице. Определить вероятность того, что шар с номером два будет извлечен при втором извлечении.Решение.
Событие А: извлекли первый шар с номером 1
(вероятность равна 1/5), то его не вернут,
и вероятность вынуть затем шар №2 равна 1/4.
Р(А) =1/5*1/4=1/20.
Событие В: извлекли шар №"2 с вероятность 1/5, осталось 4 шара, вероятность вторым вынуть шар №2 равна 0.
Р(В)=1/5*0=0
Событие С: первым извлекли шар №3 или №4 или №5. Вероятность равна 3/5, вероятность вынуть вторым шар №2 равна 1/5 (так первый шар вернули).