Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Решение квадратных уравнений. Интерактивная презентация для самостоятельного изучения темы
Содержание
- 1. Решение квадратных уравнений. Интерактивная презентация для самостоятельного изучения темы
- 2. Что такое блок-схема? Блок-схема – это
- 3. Что и как изображать на блок-схеме?Начало и конец алгоритма:Поток управления:Ввод данных:Вывод данных:НК
- 4. Что и как изображать на блок-схеме? (продолжение)Простые безусловные действия:Условные действия:
- 5. Что такое квадратное уравнение?Уравнение вида
- 6. Что такое дискриминант?Выражение
- 7. Находим коэффициенты а, b и с из
- 8. Список примеровПример 1Пример 2Пример 3Контрольное заданиеВ начало
- 9. Пример 1Нa, b, cD = b2 –
- 10. Пример 2Нa, b, cD = b2 –
- 11. Пример 3Нa, b, cD = b2 –
- 12. Контрольное заданиеРешите уравнения:Назад
- 13. Скачать презентанцию
Что такое блок-схема? Блок-схема – это графический способ записи алгоритма. Вспомни: что такое алгоритм? Какие еще способы записи алгоритма ты знаешь?
Слайды и текст этой презентации
Слайд 2Что такое блок-схема?
Блок-схема – это графический способ записи
алгоритма.
алгоритма ты знаешь?
Слайд 3Что и как изображать на блок-схеме?
Начало и конец алгоритма:
Поток управления:
Ввод
данных:
Вывод данных:
Н
К
Слайд 4Что и как изображать на блок-схеме?
(продолжение)
Простые безусловные действия:
Условные действия:
Слайд 5Что такое квадратное уравнение?
Уравнение вида
, где
называется квадратным уравнением.
Решить уравнение – значит найти все его корни или установить, что их нет.
Слайд 6Что такое дискриминант?
Выражение
называется дискриминантом квадратного уравнения
Дискриминант определяет число корней данного уравнения.
Слайд 7
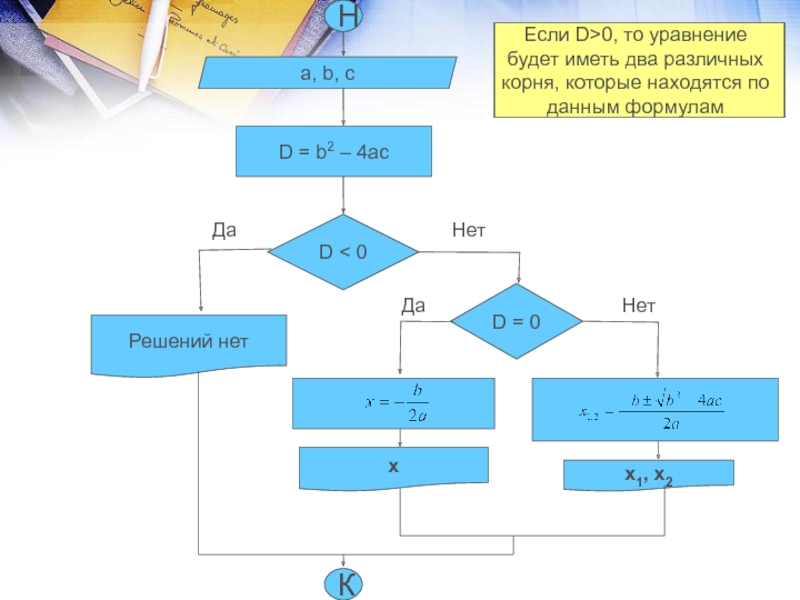
Находим коэффициенты а, b и с из уравнения
Н
a, b, c
D
= b2 – 4ac
D < 0
Да
Нет
Решений нет
Нет
D = 0
Да
х1, х2
х
Находим
значение дискриминантаПроверяем, выполняется ли данное условие
Если D<0, то уравнение не имеет действительных корней
Если это условие не выполняется, то D>0 или D=0
Если D=0, то уравнение будет иметь единственный корень, который находится по данной формуле
Если D>0, то уравнение будет иметь два различных корня, которые находятся по данным формулам
К
Слайд 9Пример 1
Н
a, b, c
D = b2 – 4ac
D < 0
Решений
нет
D = 0
х
х1, х2
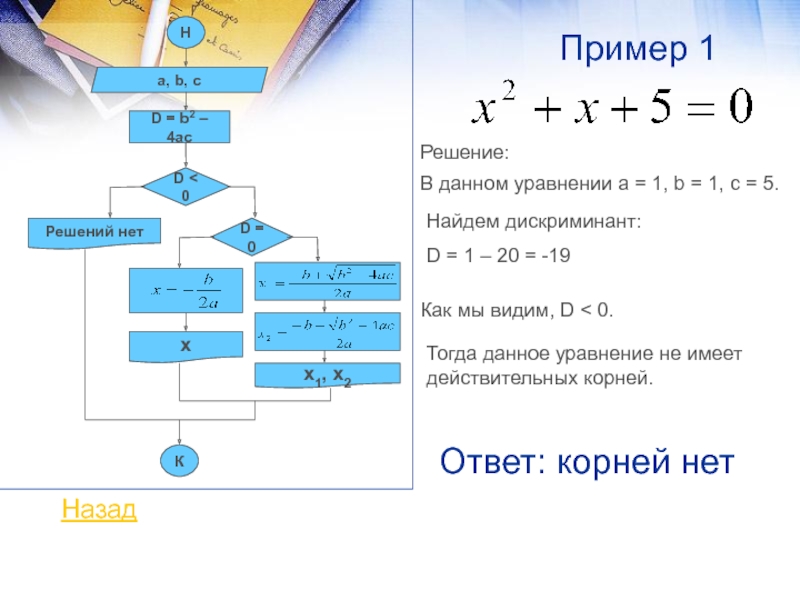
В данном уравнении а = 1, b
= 1, с = 5.Решение:
Найдем дискриминант:
D = 1 – 20 = -19
Как мы видим, D < 0.
Тогда данное уравнение не имеет действительных корней.
Ответ: корней нет
Назад
К
Слайд 10Пример 2
Н
a, b, c
D = b2 – 4ac
D < 0
Решений
нет
D = 0
х
х1, х2
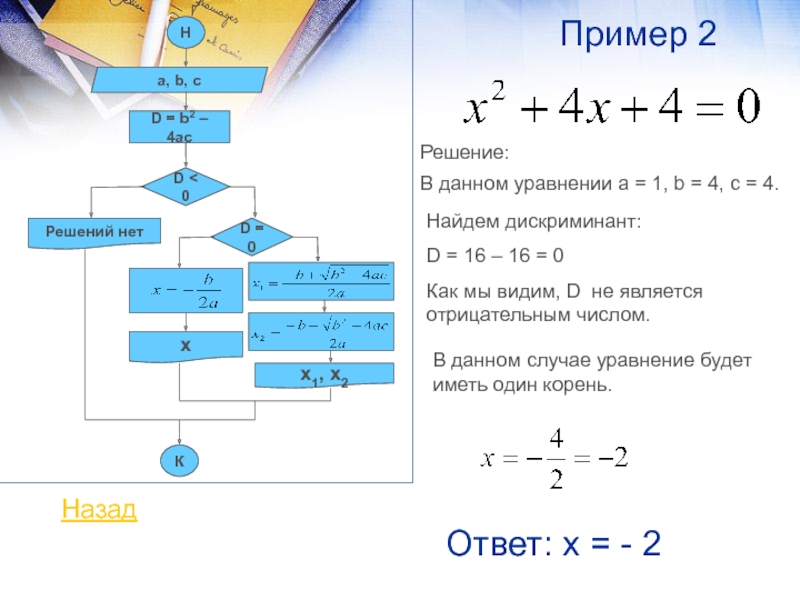
В данном уравнении а = 1, b
= 4, с = 4.Решение:
Найдем дискриминант:
D = 16 – 16 = 0
Как мы видим, D не является отрицательным числом.
В данном случае уравнение будет иметь один корень.
Ответ: х = - 2
Назад
К
Слайд 11Пример 3
Н
a, b, c
D = b2 – 4ac
D < 0
Решений
нет
D = 0
х
х1, х2
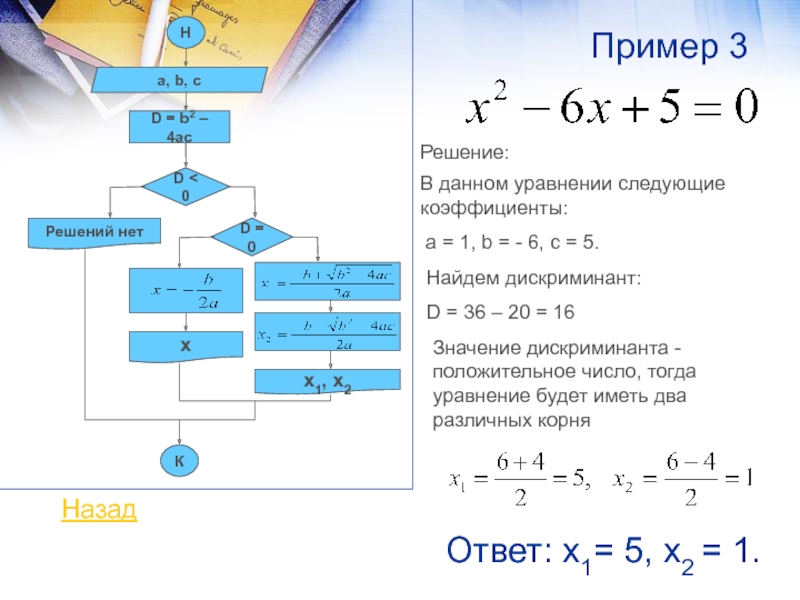
В данном уравнении следующие коэффициенты:
а =
1, b = - 6, с = 5.Решение:
Найдем дискриминант:
D = 36 – 20 = 16
Ответ: х1= 5, х2 = 1.
Значение дискриминанта - положительное число, тогда уравнение будет иметь два различных корня
Назад
К
