Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Из истории тригонометрии
Содержание
- 1. Из истории тригонометрии
- 2. Проблема:Ученикам часто кажется, что тригонометрия – это
- 3. Тригонометрические функции Сам термин «тригонометрические функции» введён Клюгелем в 1770.
- 4. Тригонометрические функции — элементарные функции — элементарные функции, которые исторически возникли
- 5. К тригонометрическим функциям относятся:прямые тригонометрические функциисинус (sin x)косинус
- 6. Кроме упомянутых существуют также редко используемые тригонометрические
- 7. Остальные четыре функции на вещественной оси также
- 8. Древняя ГрецияПотребность в решении треугольников раньше всего
- 9. Слайд 9
- 10. Значительный вклад в развитие тригонометрии внесли арабские
- 11. Длительную историю имеет понятие синус. Фактически различные
- 12. В римский период эти отношения достаточно систематично
- 13. Слово синус появилось в математике далеко не сразу. Этот
- 14. Слайд 14
- 15. Слово косинус намного моложе. Косинус – это
- 16. Слайд 16
- 17. Синус острого угла в прямоугольном треугольнике —
- 18. Слайд 18
- 19. История развития тангенса Тангенсы возникли в связи
- 20. Слайд 20
- 21. Не сохранилась. По видимому, его "родил" тангенс, когда как-то перевернулся (шутка).История возникновения котангенса
- 22. Тангенс острого угла в прямоугольном треугольнике —
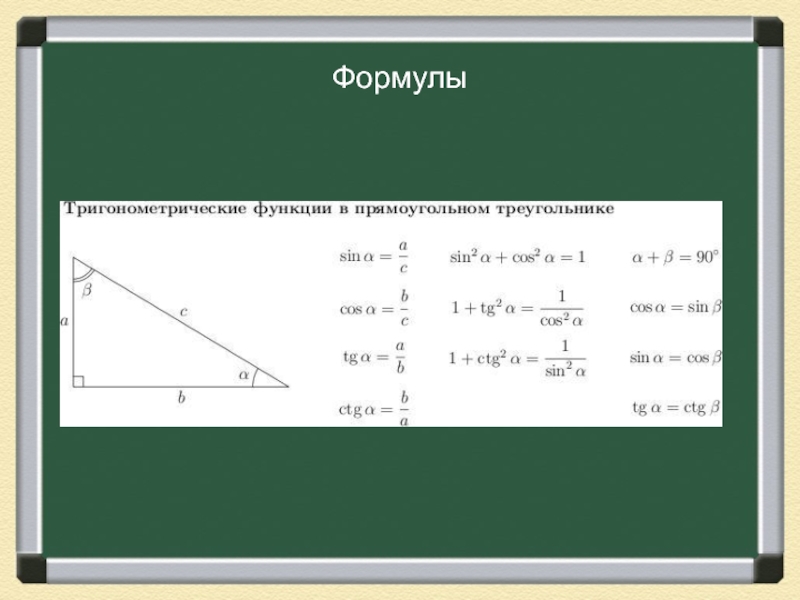
- 23. Формулы
- 24. Спасибо за внимание!
- 25. Скачать презентанцию
Проблема:Ученикам часто кажется, что тригонометрия – это скучный набор формул и графиков. И они не догадываются, что многое из того что нас окружает: восход и заход Солнца, затмения и движения планет,
Слайды и текст этой презентации
Слайд 4
Тригонометрические функции — элементарные функции — элементарные функции, которые исторически возникли при рассмотрении прямоугольных треугольников — элементарные
функции, которые исторически возникли при рассмотрении прямоугольных треугольников и выражали зависимости сторон
этих треугольников от острых углов при гипотенузе — элементарные функции, которые исторически возникли при рассмотрении прямоугольных треугольников и выражали зависимости сторон этих треугольников от острых углов при гипотенузе (или, что эквивалентно, зависимость хорд — элементарные функции, которые исторически возникли при рассмотрении прямоугольных треугольников и выражали зависимости сторон этих треугольников от острых углов при гипотенузе (или, что эквивалентно, зависимость хорд и высот от центрального угла — элементарные функции, которые исторически возникли при рассмотрении прямоугольных треугольников и выражали зависимости сторон этих треугольников от острых углов при гипотенузе (или, что эквивалентно, зависимость хорд и высот от центрального угла в круге — элементарные функции, которые исторически возникли при рассмотрении прямоугольных треугольников и выражали зависимости сторон этих треугольников от острых углов при гипотенузе (или, что эквивалентно, зависимость хорд и высот от центрального угла в круге). Эти функции нашли широчайшее применение в самых разных областях науки. Впоследствии определение тригонометрических функций было расширено, их аргументом теперь может быть произвольное вещественное — элементарные функции, которые исторически возникли при рассмотрении прямоугольных треугольников и выражали зависимости сторон этих треугольников от острых углов при гипотенузе (или, что эквивалентно, зависимость хорд и высот от центрального угла в круге). Эти функции нашли широчайшее применение в самых разных областях науки. Впоследствии определение тригонометрических функций было расширено, их аргументом теперь может быть произвольное вещественное или даже комплексное число.Наука, изучающая свойства тригонометрических функций, называется тригонометрией.
Слайд 5К тригонометрическим функциям относятся:
прямые тригонометрические функции
синус (sin x)
косинус (cos x)
производные тригонометрические функции
тангенс
(tg x)
котангенс (ctg x)
другие тригонометрические функции
секанс (sec x)
косеканс (cosec x)
В западной литературе тангенс, котангенс
и косеканс обозначаются tan x, cot x, csc x.Слайд 6
Кроме упомянутых существуют также редко используемые тригонометрические функцииКроме упомянутых существуют
также редко используемые тригонометрические функции (версинус и т.д.), а также обратные тригонометрические
функции(арксинус, арккосинус и т. д.), рассматриваемые в отдельных статьях.Синус и косинус вещественного аргумента являются периодическими непрерывнымиСинус и косинус вещественного аргумента являются периодическими непрерывными и неограниченно дифференцируемыми
вещественнозначными функциями.
Слайд 7Остальные четыре функции на вещественной оси также вещественнозначные, периодические и
неограниченно дифференцируемые на области определения, но не непрерывные. Тангенс и
секанс имеют разрывы второго рода в точках ±πn + π/2, а котангенс и косеканс — в точках ±πn.Слайд 8Древняя Греция
Потребность в решении треугольников раньше всего возникла в астрономии:
и в течении долгого времени тригонометрия развивалась изучалась как один
из отделов астрономии. Насколько известно: способы решения треугольников (сферических) первые были письменно изложены греческим астрономом Гиппархом в середине 2 века до н.э. Наивысшими достижениями греческая тригонометрия обязана астроному Птолемею (2 век н.э.), создателю геоцентрической системы мира, господствовавшей до Коперника.Слайд 10Значительный вклад в развитие тригонометрии внесли арабские ученые Аль-Батани (850-929)
и Абу-ль-Вафа, Мухамед-бен Мухамед (940-998), который составил таблицы синусов и
тангенсов через 10’ с точностью до 1/604. Теорему синусов уже знали индийский ученый Бхаскара (р. 1114, год смерти неизвестен) и азербайджанский астроном и математик Насиреддин Туси Мухамед (1201-1274). Кроме того, Насиреддин Туси в своей работе «Трактат о полном четырехстороннике» изложил плоскую и сферическую тригонометрию как самостоятельную дисциплину.Слайд 11Длительную историю имеет понятие синус. Фактически различные отношения отрезков треугольника
и окружности (а по существу, и тригонометрические функции) встречаются уже
в III веке до н.э. в работах великих математиков Древней Греции – Евклида, Архимеда, Апполония Пергского.Слайд 12
В римский период эти отношения достаточно систематично исследовались Менелаем (I
век н.э.), хотя и не приобрели специального названия. Современный синус
a, например, изучался как полухорда, на которую опирается центральный угол величиной a, или как хорда удвоенной дуги.Слайд 13Слово синус появилось в математике далеко не сразу. Этот термин имеет свою
длительную (начиная с I-II вв.) и интересную историю. Зарождение тригонометрии
связано с именами александрийских астрономов и в первую очередь с именем Клавдия Птолемея.История понятия синуса
Слайд 15Слово косинус намного моложе. Косинус – это сокращение латинского выражения
completely sinus, т. е. “дополнительный синус” (или иначе “синус дополнительной
дуги”; cosa = sin( 90° - a)). Современное обозначение синуса sin и косинуса cos введено Леонардом Эйлером в XVIII веке.История понятия косинуса
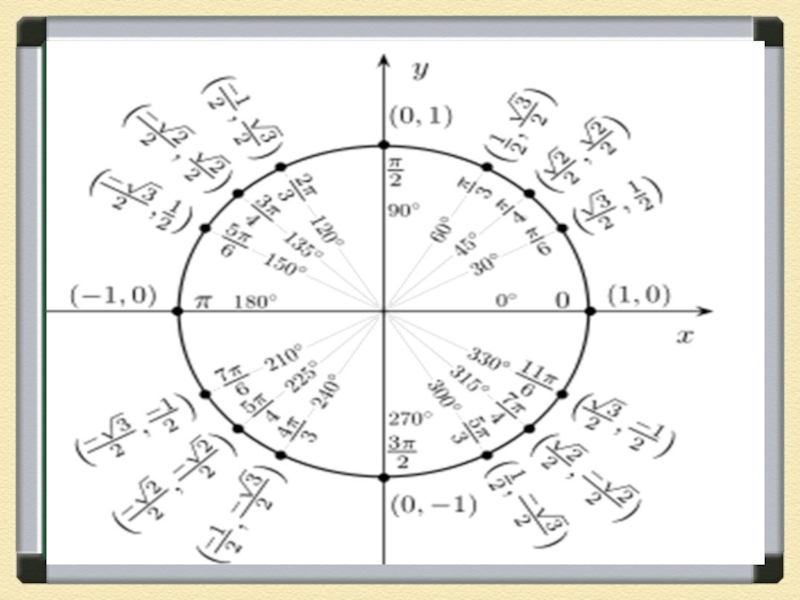
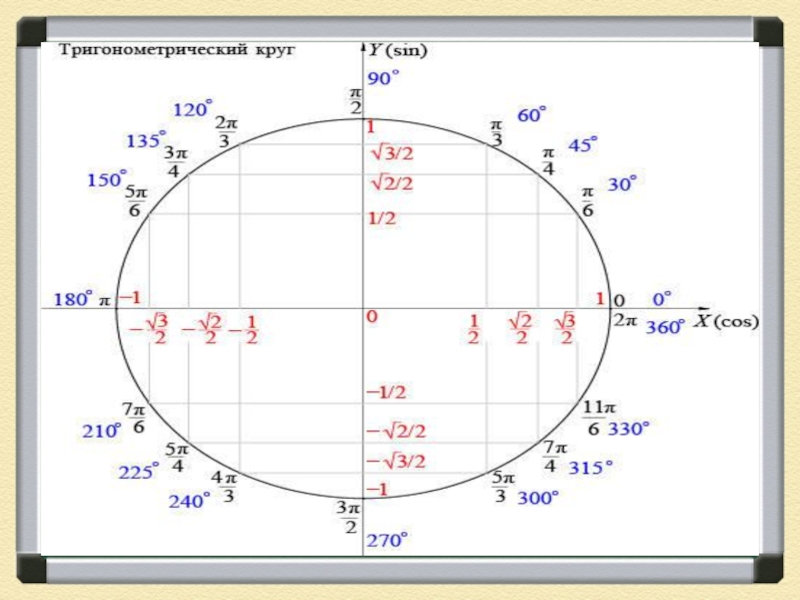
Слайд 17Синус острого угла в прямоугольном треугольнике — это отношение противолежащего
катета к гипотенузе:
Косинус острого угла в прямоугольном треугольнике — отношение
прилежащего катета к гипотенузе:прямые тригонометрические функции
синус (sin x), косинус (cos x)
Слайд 19История развития тангенса
Тангенсы возникли в связи с решением задачи
об определении длины тени. Тангенс (а также котангенс) введен в
X веке арабским математиком Абу-ль-Вафой, который составил и первые таблицы для нахождения тангенсов и котангенсов. Однако эти открытия долгое время оставались неизвестными европейским ученым, и тангенсы были заново открыты лишь в XIV веке немецким математиком, астрономом Регимонтаном (1467 г.). Он доказал теорему тангенсов. Региомонтан составил также подробные тригонометрические таблицы; благодаря его трудам плоская и сферическая тригонометрия стала самостоятельной дисциплиной и в Европе.Название «тангенс», происходящее от латинского tanger (касаться), появилось в 1583 г. Tangens переводится как «касающийся» (линия тангенсов – касательная к единичной окружности).
Слайд 21Не сохранилась. По видимому, его "родил" тангенс, когда как-то перевернулся
(шутка).
История возникновения котангенса
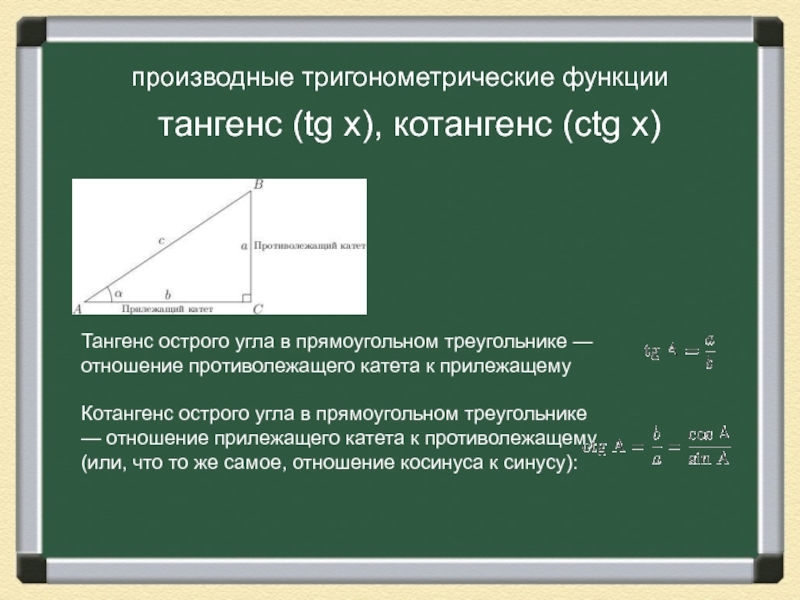
Слайд 22Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета
к прилежащему
Котангенс острого угла в прямоугольном треугольнике — отношение прилежащего
катета к противолежащему (или, что то же самое, отношение косинуса к синусу):производные тригонометрические функции
тангенс (tg x), котангенс (ctg x)