Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математическое описание случайных явлений (часть 2)
Содержание
- 1. Математическое описание случайных явлений (часть 2)
- 2. пункт 28. Вероятности элементарных
- 3. Пункт 28 №1. Случайный опыт может
- 4. Пункт 28 №2. Неправильная игральная кость
- 5. Пункт 28 №3. Все элементарные события
- 6. Пункт 28 №4. Все элементарные события
- 7. Пункт 28 №5. В каждом из
- 8. Вариант АПо условию: в первом опыте элементарных
- 9. Правильный ответ к варианту АБольшая вероятность элементарного
- 10. Вариант БВ первом опыте элементарных событий меньше,
- 11. Вариант ВВ этих опытах элементарных событий поровну;Вероятность
- 12. Пункт 28 №6. При подбрасывании монеты
- 13. Пункт 28 №7. Симметричную монету подбрасывают несколько
- 14. Пункт 28 №7. Симметричную монету подбрасывают несколько
- 15. В)* При подбрасывании монеты 10 раз может
- 16. Пункт 28 №8. Три богатыря Илья Муромец,
- 17. Введем обозначения:На первом месте всегда будем записывать
- 18. Пункт 28 №9. Случайный опыт состоит в
- 19. Пункт 28 №10. Три первоклассника по очереди
- 20. Пункт 28 №11. Три первоклассника по очереди
- 21. Пункт 28 №12. Игральную кость подбрасывают несколько
- 22. Авторы решения задач №№1; 2; 3; 4
- 23. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Математическое описание случайных явлений
Часть 2
Решения задач
Проект учащихся 8А класса
ГОУ
СОШ №420 ЮАО г. Москвы
Слайд 3Пункт 28 №1. Случайный опыт может закончиться одним из трех
элементарных событий: а, Ь или с. Чему равна вероятность элементарного
события с, еслиа) ,
б) ,
в) ,
г)* ,
Какие значения
может принимать р .
Сумма вероятностей всех элементарных событий равна 1.
А)P(c)=1-1/2 - 1/3=1/6
Б)Р(с)=1-0,4 - 0,2=0,4
В)Р(с)=1-0,1- 0,01=0,89
Г)*Р(с)=1- p – (0,8-p)=
=1-p-0,8+p= 0,2
Слайд 4Пункт 28 №2. Неправильная игральная кость такова, что вероятность выбросить
грань, на которой 1 очко, равна 1/4 , вероятность выбросить
грань с 2 очками равна 1/12 , с 3 очками — равна 1/4, с 5 очками — равна1/12, а вероятность выбросить грань с 6 очками равна 1/6. Найдите вероятность выбросить грань с 4 очками.Сумма вероятностей всех элементарных событий равна 1.
Вероятность выпадения четверки равна
1– 1/4 - 1/12 – 1/4 - 1/12 - 1/6=1/6
Слайд 5Пункт 28 №3. Все элементарные события случайного эксперимента равновозможны. Найдите
вероятность каждого элементарного события, если их общее число равно:
а) 25; 6)17; в) 100.Так как события равновозможны, то:
А) Вероятность каждого события равна 1/25
Б) Вероятность каждого события равна 1/17
В) Вероятность каждого события равна 1/100
Слайд 6Пункт 28 №4. Все элементарные события случайного опыта равновозможны. Сколько
элементарных событий в этом опыте, если вероятность одного из них
равна: а) 1/3 ; 6)0,1; в) 0,125; г) 1/nЕсли вероятность каждого из событий равна 1/n, то число элементарных событий равно n.
А) вероятность 1/3, всего событий 3.
Б) вероятность 0,1=1/10 , всего событий 10.
В) вероятность 0,125=1/8, всего событий 8.
Г) вероятность 1/n, всего событий n.
Слайд 7Пункт 28 №5.
В каждом из двух случайных опытов
все элементарные события равновозможны. В каком из этих опытов вероятность
элементарного события больше, если:а) в первом опыте элементарных событий больше, чем во втором; б) в первом опыте элементарных событий меньше, чем во втором; в) в этих опытах элементарных событий поровну?
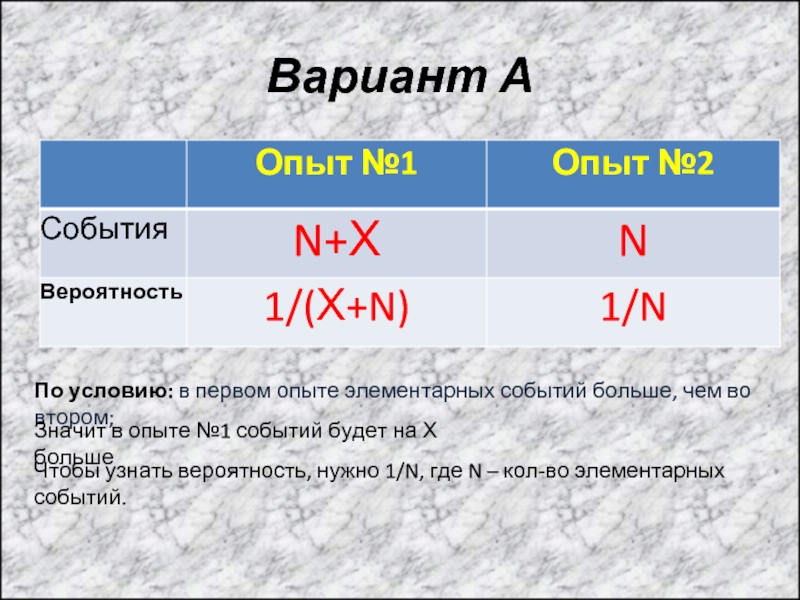
Слайд 8Вариант А
По условию: в первом опыте элементарных событий больше, чем
во втором;
Значит в опыте №1 событий будет на Х
большеЧтобы узнать вероятность, нужно 1/N, где N – кол-во элементарных событий.
Слайд 9Правильный ответ к варианту А
Большая вероятность элементарного события будет в
опыте №2, т.к. 1/N больше чем 1/(Х+N)
Слайд 10Вариант Б
В первом опыте элементарных событий меньше, чем во втором;
В опыте №2 вероятность будет на Х больше, чем в
№1Вероятность равна 1/N, где N – количество элементарных событий.
Большая вероятность элементарного события будет в опыте №1, т.к. 1/N больше чем 1/(Х+N)
Слайд 11Вариант В
В этих опытах элементарных событий поровну;
Вероятность равна 1/N, где
N – количество элементарных событий.
В опыте №2 вероятность будет равна
вероятности в №1Вероятности в обоих опытах равны
Слайд 12Пункт 28 №6. При подбрасывании монеты будем обозначать буквой
О выпадение орла и буквой Р выпадение решки. Подбросим симметричную
монету два раза. Равновозможны ли элементарные события ОО, РО, ОР и РР? Найдите их вероятности.Эти события равновозможны, так как в результате опыта может наступить любое из этих элементарных событий.
Так как событий всего 4 и они равновозможны, то вероятность каждого равна ¼.
Слайд 13Пункт 28 №7. Симметричную монету подбрасывают несколько раз. Найдите вероятность
элементарных событий при: А) 3 бросаниях б) 4 бросаниях В)*
10 бросанияхЕсли число элементарных событий равно N, то вероятность каждого из них равна 1/N.
При 3-х подбрасываниях монеты может выпасть: РРР ,РРО, РОР РОО,ООО. ОРР, ОРО, ООР.
Всего элементарных событий 8, значит вероятность одного элементарного события равна 1/8.
Слайд 14Пункт 28 №7. Симметричную монету подбрасывают несколько раз. Найдите вероятность
элементарных событий при: А) 3 бросаниях б) 4 бросаниях В)*
10 бросанияхБ) При 4 бросаниях монеты может выпасть:
Всего элементарных событий 16, значит вероятность одного элементарного события равна 1/16
Слайд 15В)* При подбрасывании монеты 10 раз может выпасть 1024 различных
комбинаций.
Всего элементарных событий 1024, значит, вероятность одного элементарного события равна
1/1024Пункт 28 №7. Симметричную монету подбрасывают несколько раз. Найдите вероятность элементарных событий при:
а) 3 бросаниях б) 4 бросаниях в)* 10 бросаниях
Слайд 16Пункт 28 №8.
Три богатыря Илья Муромец, Алеша Попович и
Добрыня Никитич ехали по дороге и увидели развилку, а на
ней — придорожный камень с предупреждением:Направо поедешь — коня потеряешь,
Налево поедешь — копье потеряешь,
Прямо поедешь — головы не снесешь.
Богатыри разделились, и каждый поехал
своей дорогой. Придумайте систему
обозначений для элементарных событий
этого опыта, запишите все элементарные
события. Считая их равновозможными,
найдите вероятность каждого из них.
Слайд 17Введем обозначения:
На первом месте всегда будем записывать путь Ильи Муромца,
на втором - Алеши Поповича
на третьем - Добрыни Никитича.
Направления будем
обозначать цифрами:Направо – 1
Налево – 2
Прямо – 3
Список элементарных событий
123, 132, 213, 231, 312, 321
Всего 6 элементарных событий
Так как они равновозможны,
вероятность каждого равна 1/6.
Слайд 18Пункт 28 №9.
Случайный опыт состоит в том, что Красная
Шапочка идет от домика мамы до домика бабушки. Красная Шапочка
может идти только по дорожкам слева направо. Схема дорожек показана на рис. 6. Каждая дорожка обозначена буквой. Элементарным событием в этом опыте является выбранный путь. Например, ах или bz.Считая, что все элементарные события равновозможны, найдите вероятность каждого из них.
Всего 12 путей:
ax, ay, az, at
bx, by, bz, bt
cx, cy, cz, ct
а т.к. события равно возможны, то
dероятность каждого события равна 1/12
Слайд 19Пункт 28 №10.
Три первоклассника по очереди покупают воздушные шарики.
Каждый из них покупает шарик одного из двух цветов: зеленого
(З) или синего (С). Выпишите элементарные события этого эксперимента. Считая, что все они равновозможны, найдите вероятность каждого из них.Возможные комбинации
ззз ззс зсз сзз зсс сзс ссз ссс
Так как события равновозможны, то вероятность каждого из них равна 1/8
ссс
Слайд 20Пункт 28 №11.
Три первоклассника по очереди покупают фломастеры. Каждый
из них покупает фломастер одного из трех цветов: зеленого (З),
синего (С) или красного (К). Сколько у этого опыта элементарных событий? Считая, что все элементарные события равновозможны, найдите вероятность каждого из них.Возможные комбинации
ЗСК ЗКС СЗК КЗС СКЗ КСЗ
ККЗ КЗК ЗКК ССЗ СЗС ЗСС
ЗЗК ЗКЗ КЗЗ ЗЗС ЗСЗ СЗЗ
ССК СКС КСС КСК СКК ККС .
ККК ССС ЗЗЗ Всего 27 вариантов.
Так как события равновозможны, то вероятность каждого из них равна 1/27.
Слайд 21Пункт 28 №12.
Игральную кость подбрасывают несколько раз. Равновозможны ли
элементарные события такого опыта? Найдите вероятность каждого элементарного события при:
а) З бросаниях; 6) 4 бросаниях.Появление одного из 6 чисел на каждой кости равновозможны.
А) Всего событий 6∙6∙6=216,
а так как события равновозможны, то вероятность каждого из них равна 1/216.
Б) Всего событий 6∙6∙6∙6=1296,
а так как события равновозможны, то вероятность каждого из них равна 1/1296.
Слайд 22Авторы решения задач
№№1; 2; 3; 4 Милехина Ксения
№№6; 7; 11;
12 Милехина Алена
№5 Силаев Леонид
№8 Перглер Илья
№9 Лазуренков Дима
№10 Андрухов
ИванНа фотографиях учащиеся нашего класса на уроке компьютерного эксперимента по теории вероятностей