Изучение темы "Пирамида"

Содержание

1. Изучение темы "Пирамида"
2. Пирамида Пирамидой называется многогранник, который состоит
3. Высотой пирамиды называется перпендикуляр, опущенный из
4. Правильная
5. Боковая поверхность правильной пирамиды
6. З а д а
7. Слайд 7
8. Слайд 8
9. Слайд 9
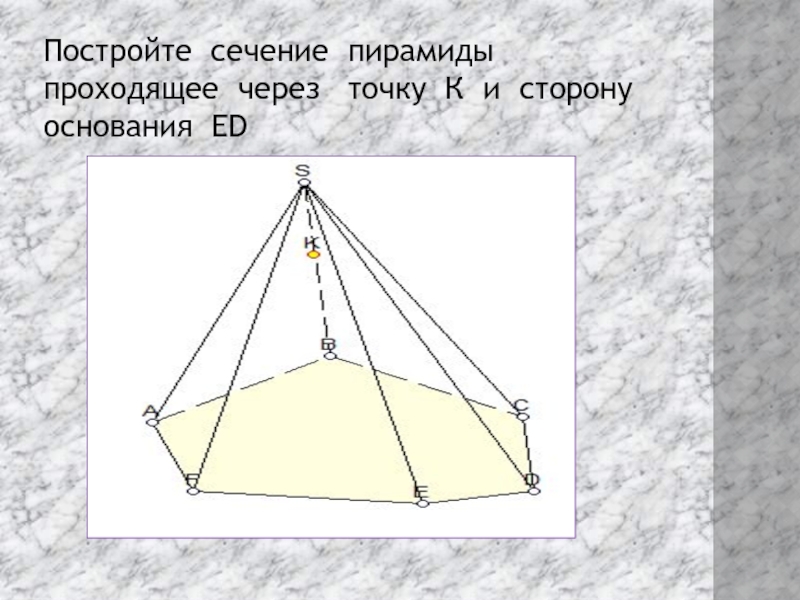
10. Постройте сечение пирамиды проходящее через точку К и сторону основания ED
11. Скачать презентанцию

Пирамида Пирамидой называется многогранник, который состоит из плоского многоугольника - основания пирамиды , точки, не лежащей в плоскости основания, - вершины пирамиды и всех отрезков, соединяющих вершину пирамиды

Слайды и текст этой презентации

Слайд 1 Пирамида

Подготовила:
учитель математики
Ильичёвской ОШ 1-3 ст.
Советского района

АР Крым
Мустафаева Асие Асановна

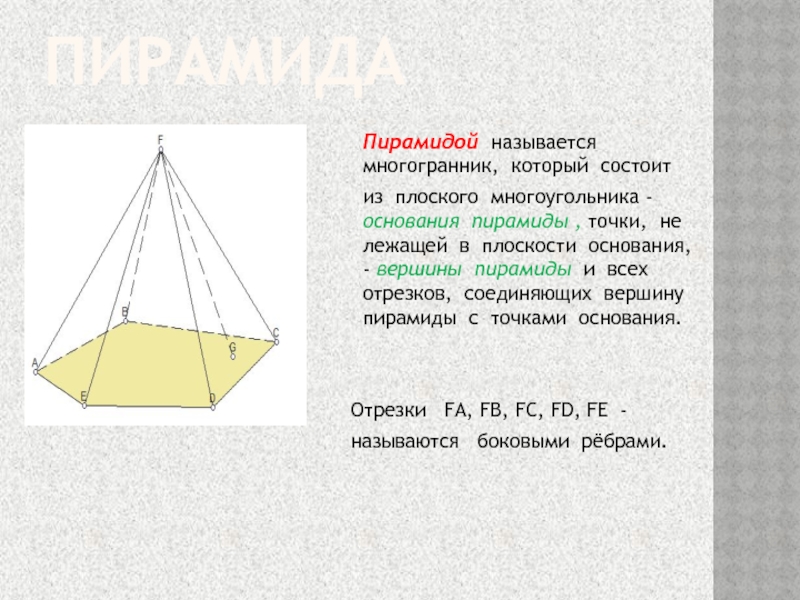
Слайд 2Пирамида
Пирамидой называется многогранник, который состоит
из

плоского многоугольника - основания пирамиды , точки, не лежащей в

плоскости основания, - вершины пирамиды и всех отрезков, соединяющих вершину пирамиды с точками основания.

Отрезки FA, FB, FC, FD, FE -
называются боковыми рёбрами.

Пирамида Пирамидой называется многогранник, который состоит из плоского многоугольника - основания пирамиды , точки,

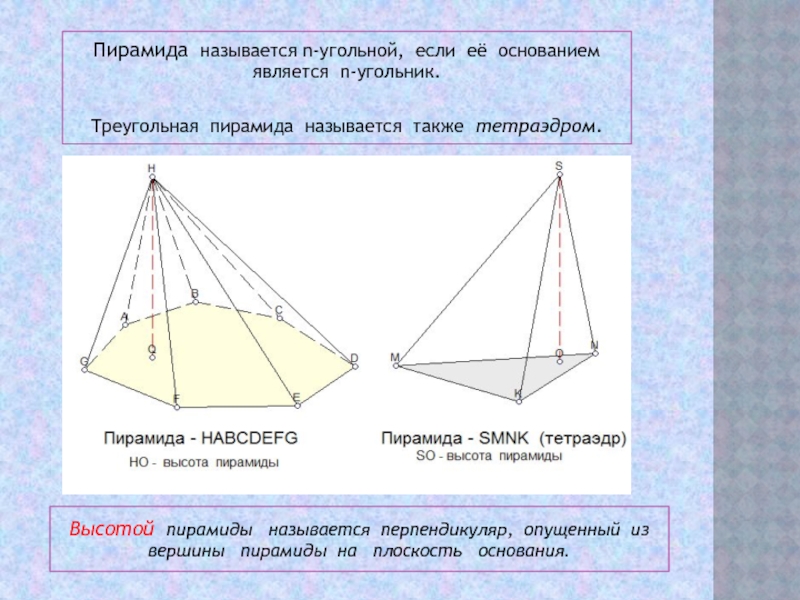
Слайд 3Высотой пирамиды называется перпендикуляр, опущенный из вершины пирамиды

на плоскость основания.
Пирамида называется n-угольной, если её основанием

является n-угольник.

Треугольная пирамида называется также тетраэдром.

Высотой пирамиды называется перпендикуляр, опущенный из вершины пирамиды на плоскость основания.Пирамида называется n-угольной,

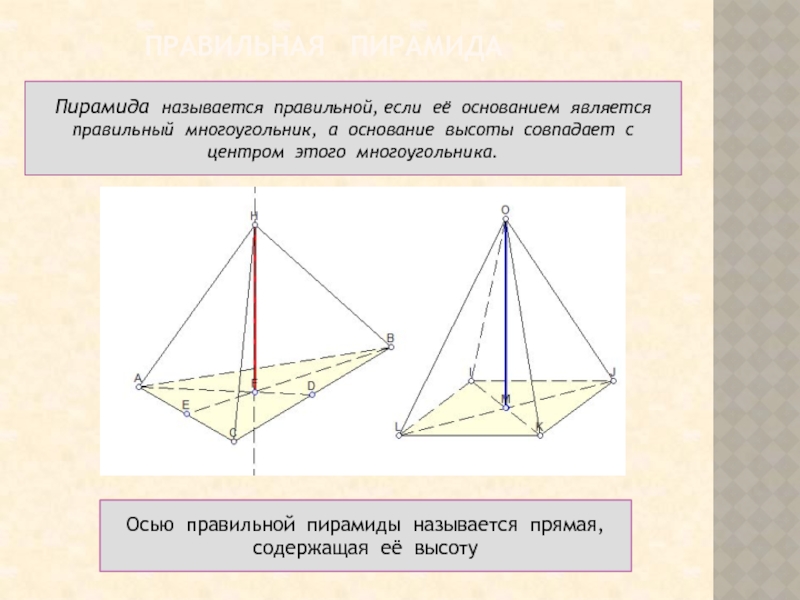
Слайд 4 Правильная пирамида
Пирамида называется

правильной, если её основанием является правильный многоугольник, а основание высоты

совпадает с центром этого многоугольника.

Осью правильной пирамиды называется прямая, содержащая её высоту

Правильная пирамидаПирамида называется правильной, если её основанием является правильный многоугольник,

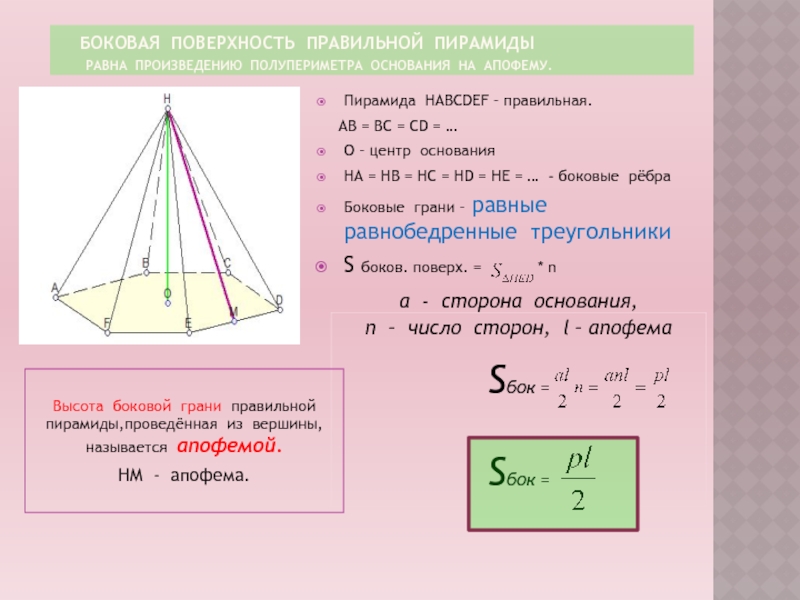
Слайд 5 Боковая поверхность правильной пирамиды

равна произведению полупериметра основания на апофему.
a - сторона основания,
n –

число сторон, l – апофема

Sбок =

Sбок =

Высота боковой грани правильной пирамиды,проведённая из вершины, называется апофемой.
НМ - апофема.

Пирамида HABCDEF – правильная.
АВ = ВС = СD = …
О – центр основания
HA = HB = HC = HD = HE = … - боковые рёбра
Боковые грани – равные равнобедренные треугольники
S боков. поверх. = * n

Боковая поверхность правильной пирамиды равна произведению полупериметра основания на апофему.a

Слайд 6 З а д а ч а

Р Е Ш

Е Н И Е

Радиус окружности , описанной
около правильного четырёхугольника

R = , где а – сторона основания

= , а = 6 см.

Р = 24 см. , апофема l = 5 см.

S бок.= , S = .

S = 60 .

О т в е т: 60 .

Радиус окружности, описанной около основания правильной четырёхугольной пирамиды, равен
см, а апофема – 5 см.
Найдите площадь боковой поверхности.

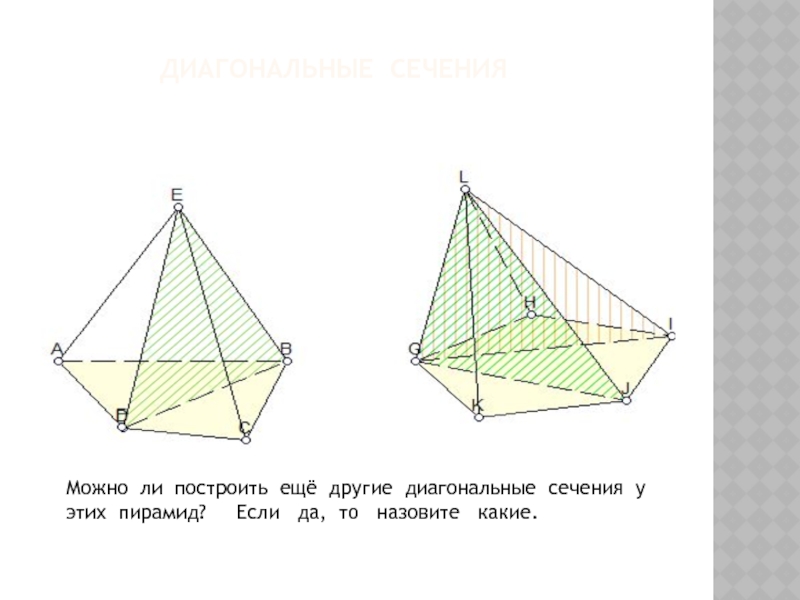
Слайд 7 Диагональные сечения
Можно ли

построить ещё другие диагональные сечения у этих пирамид?

Если да, то назовите какие.

Диагональные сеченияМожно ли построить ещё другие диагональные сечения у этих

Слайд 8

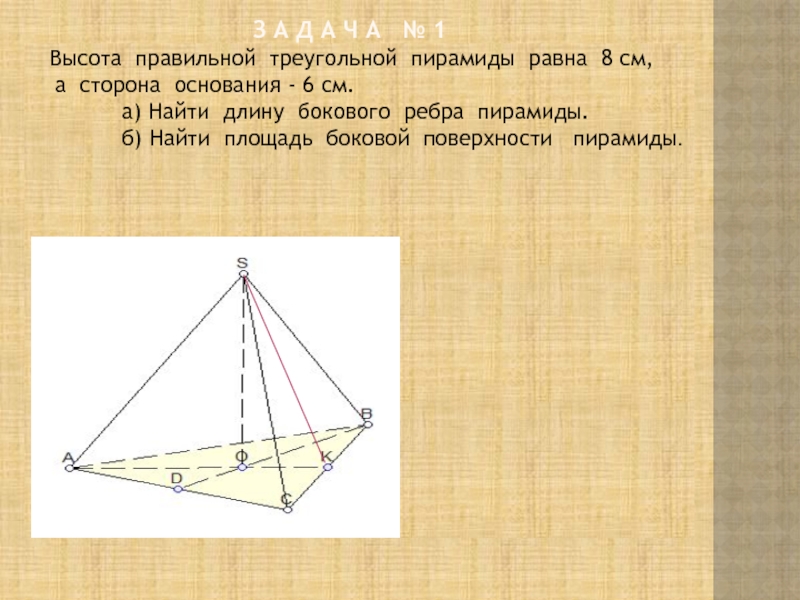
З А Д А Ч

А № 1

Высота правильной треугольной пирамиды равна 8 см,
а сторона основания - 6 см.
а) Найти длину бокового ребра пирамиды.
б) Найти площадь боковой поверхности пирамиды.

Слайд 9

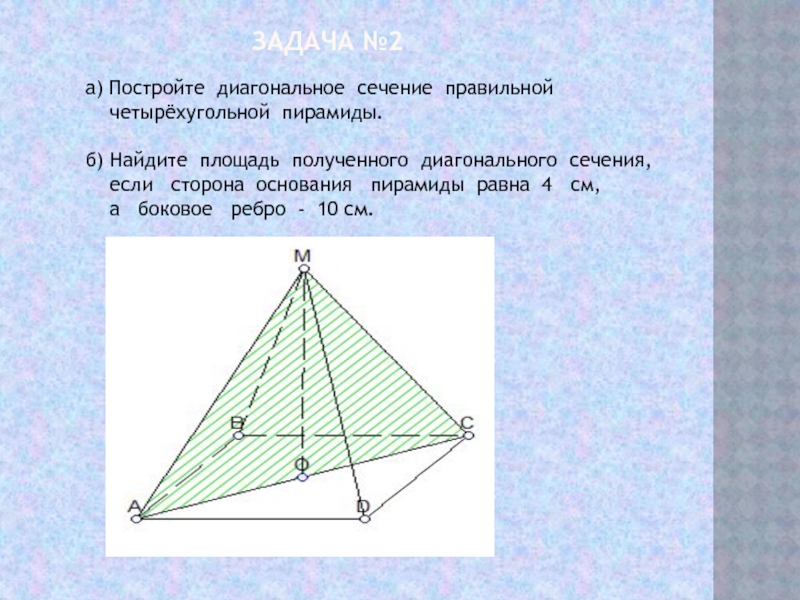
Задача №2
а) Постройте

диагональное сечение правильной
четырёхугольной пирамиды.

б) Найдите площадь полученного диагонального сечения,
если сторона основания пирамиды равна 4 см,
а боковое ребро - 10 см.