Знакомьтесь, уравнение

Содержание

1. Знакомьтесь, уравнение
2. Знакомьтесь, уравнение!Работу выполнила ученица 9-го класса Лёвина Дарья
3. Определение квадратного уравненияназывается квадратным уравнением где х
4. МОУ Тулиновская средняя общеобразовательная школаназывается дискриминантомВыражение
5. МОУ Тулиновская средняя общеобразовательная школаaх2 + вх
6. Исторические сведенияНеобходимость решать уравнения не только первой,
7. Цель исследования:Выяснить, можно ли решать квадратное уравнение с помощью циркуля и линейкиМОУ Тулиновская средняя общеобразовательная школа
8. ГипотезаПо данным действительным коэффициентам a, b, c
9. Ход исследования:1. Изучив теоретический материал учебника и
10. Задача. По
11. Ход решения задачиух(х1;0) (х2;0)FBKEAOC(0;1) S(;)(0;)МОУ Тулиновская средняя общеобразовательная школа
12. План нахождения корней квадратного уравнения с помощью
13. ух(х1;0)KEAO(0;1) S(0;)Радиус окружности больше ординаты центраВ этом
14. ух(х1;0)EAO(0;1) S(0;)Радиус окружности равен ординате центраВ этом
15. ухEAO(0;1) S(0;)Радиус окружности меньше ординаты центраВ этом
16. Примеры:а) 2x2 + 3x + 1
17. Примеры:б) x2 - 5x + 6
18. Выводы1. Квадратные уравнения можно решать с помощью
19. Способы решения квадратных уравненийИзучаемые в школе: Разложение
20. Способы решения квадратных уравненийПродвинутые способы: Способ переброски
21. Глейзер Г.И. История математики в школе. –
22. Скачать презентанцию

Знакомьтесь, уравнение!Работу выполнила ученица 9-го класса Лёвина Дарья

Слайды и текст этой презентации

Слайд 1Карл Фридрих Гаусс (1777-1855) немецкий математик, астроном, геодезист и физик,

иностранный член-корреспондент (1802) и иностранный почетный член (1824) Петербургской АН
О,

математика. В веках овеяна ты славой,
Светило всех земных светил.
Тебя царицей величавой
Недаром Гаусс окрестил.
Строга, логична, величава,
Стройна в полёте, как стрела,
Твоя немеркнущая слава
В веках бессмертье обрела.
Мы славим разум человека,
Дела его волшебных рук,
Надежду нынешнего века,
Царицу всех земных наук.
Поведать мы сегодня вам хотим
Историю возникновения того,
Что каждый школьник должен знать –
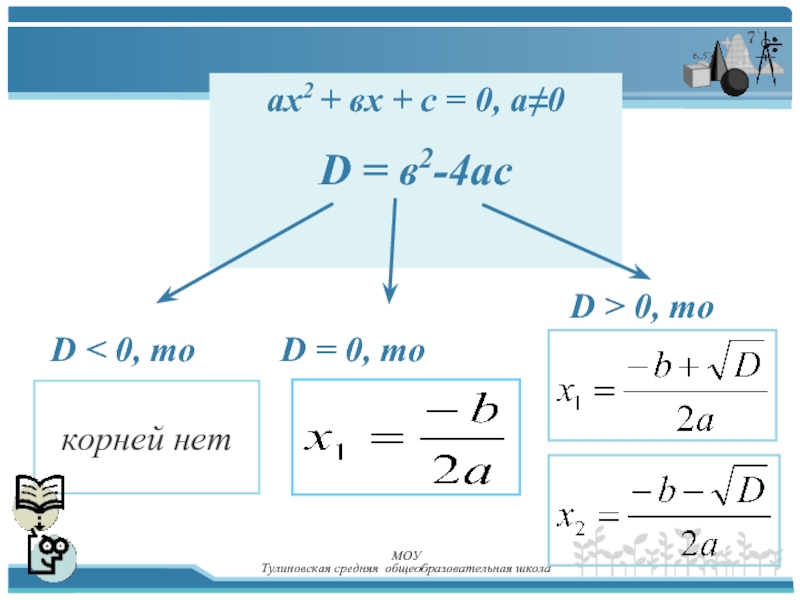
Историю квадратных уравнений,
А также их уметь решать.

Карл Фридрих Гаусс (1777-1855) немецкий математик, астроном, геодезист и физик, иностранный член-корреспондент (1802) и иностранный почетный член

Слайд 2Знакомьтесь, уравнение!
Работу выполнила
ученица 9-го класса
Лёвина Дарья

Слайд 3Определение квадратного уравнения
называется квадратным уравнением
где х – переменная,

а, b и c – некоторые числа,
причем а

≠ 0

Уравнение вида

МОУ
Тулиновская средняя общеобразовательная школа

Определение квадратного уравненияназывается квадратным уравнением где х – переменная, а, b и c – некоторые числа,

Слайд 4МОУ
Тулиновская средняя общеобразовательная школа
называется дискриминантом
Выражение

Слайд 5МОУ
Тулиновская средняя общеобразовательная школа
aх2 + вх + с =

0, а≠0
D = в2-4ас

D < 0, то
D = 0, то

D > 0, то

корней нет

Слайд 6Исторические сведения
Необходимость решать уравнения не только первой, но и второй

степени в древности была вызвана потребностью решать задачи, связанные с

нахождением площадей земельных участков и работами военного характера, с развитием астрономии и математики. Квадратные уравнения умели решать около 2000 лет до н. э. вавилоняне.

Web - Web - сайт

МОУ
Тулиновская средняя общеобразовательная школа

Исторические сведенияНеобходимость решать уравнения не только первой, но и второй степени в древности была вызвана потребностью решать

Слайд 7Цель исследования:
Выяснить, можно ли решать квадратное уравнение с помощью циркуля

и линейки
МОУ
Тулиновская средняя общеобразовательная школа

Цель исследования:Выяснить, можно ли решать квадратное уравнение с помощью циркуля и линейкиМОУ Тулиновская средняя общеобразовательная школа

Слайд 8Гипотеза
По данным действительным коэффициентам a, b, c уравнения
ax2 +

bx + c = 0 (a ≠ 0) можно определить

радиус и координаты центра окружности, пересекающей ось Ox в точках, абсциссы которых являются корнями данного уравнения

МОУ
Тулиновская средняя общеобразовательная школа

ГипотезаПо данным действительным коэффициентам a, b, c уравнения ax2 + bx + c = 0 (a ≠

Слайд 9Ход исследования:
1. Изучив теоретический материал учебника и дополнительных источников информации

выяснить, способы решения квадратных уравнений с помощью циркуля и линейки.
2.

Изучить историю квадратных уравнений.
3. Оформить результаты, сделать соответствующие выводы.

МОУ
Тулиновская средняя общеобразовательная школа

Ход исследования:1. Изучив теоретический материал учебника и дополнительных источников информации выяснить, способы решения квадратных уравнений с помощью

Слайд 10Задача.
По данным действительным коэффициентам

a, b, c уравнения
ax2 + bx + c =

0 (a ≠ 0) определить радиус и координаты центра окружности, пересекающей ось Ox в точках, абсциссы которых являются корнями данного уравнения .

МОУ
Тулиновская средняя общеобразовательная школа

Задача. По данным действительным коэффициентам a, b, c уравнения ax2 + bx

Слайд 11Ход решения задачи

у
х
(х1;0)
(х2;0)
F
B
K
E
A
O
C
(0;1)

S
(
;
)
(0;
)
МОУ
Тулиновская средняя общеобразовательная школа

Слайд 12План нахождения корней квадратного уравнения с помощью циркуля и линейки
В

системе координат построим

точки

и А (0;1).
Проведём окружность с радиусом SA.
3. Абсциссы точек пересечения окружности с осью Ох являются корнями исходного квадратного уравнения.

МОУ
Тулиновская средняя общеобразовательная школа

План нахождения корней квадратного уравнения с помощью циркуля и линейкиВ системе координат построим точки

Слайд 13
у
х
(х1;0)
K
E
A
O
(0;1)

S
(0;
)
Радиус окружности больше ординаты центра
В этом случае окружность пересекает

ось Ох в точках В(х1;0) С(х2;0)

(х2;0)
С
В
МОУ
Тулиновская

средняя общеобразовательная школа

ух(х1;0)KEAO(0;1) S(0;)Радиус окружности больше ординаты центраВ этом случае окружность пересекает ось Ох в точках В(х1;0)

Слайд 14
у
х
(х1;0)
E
A
O
(0;1)

S
(0;
)
Радиус окружности равен ординате центра
В этом случае уравнение имеет

равные действительные корни, абсцисса точки касания х1,2 =
В
МОУ
Тулиновская

средняя общеобразовательная школа

ух(х1;0)EAO(0;1) S(0;)Радиус окружности равен ординате центраВ этом случае уравнение имеет равные действительные корни, абсцисса точки касания

Слайд 15
у
х
E
A
O
(0;1)

S
(0;
)
Радиус окружности меньше ординаты центра
В этом случае окружность не

имеет общих точек с осью Ох и уравнение имеет комплексные

и сопряжённые корни х1,2 =
=

МОУ
Тулиновская средняя общеобразовательная школа

ухEAO(0;1) S(0;)Радиус окружности меньше ординаты центраВ этом случае окружность не имеет общих точек с осью Ох и

Слайд 16Примеры:

а) 2x2 + 3x + 1 = 0
Определим координаты

точки центра окружности по формулам:
x =
y =
Проведём окружность

радиуса SA, где А(0;1). Корни уравнения -1 и - 0,5.

-0,5

-1

МОУ
Тулиновская средняя общеобразовательная школа

Примеры:а) 2x2 + 3x + 1 = 0Определим координаты точки центра окружности по формулам: x =y

Слайд 17Примеры:

б) x2 - 5x + 6 = 0
Определим координаты

точки центра окружности по формулам:
x =
y =
Проведём окружность

радиуса SA, где А(0;1). Корни уравнения 2 и 3.

МОУ
Тулиновская средняя общеобразовательная школа

Примеры:б) x2 - 5x + 6 = 0Определим координаты точки центра окружности по формулам: x =y

Слайд 18Выводы
1. Квадратные уравнения можно решать с помощью циркуля и линейки.
2.

По данным действительным коэффициентам a, b, c уравнения
ax2 +

bx + c = 0 (a ≠ 0) можно определить радиус и координаты центра окружности, пересекающей ось Ox в точках, абсциссы которых являются корнями данного уравнения

МОУ
Тулиновская средняя общеобразовательная школа

Выводы1. Квадратные уравнения можно решать с помощью циркуля и линейки.2. По данным действительным коэффициентам a, b, c

Слайд 19Способы решения квадратных уравнений
Изучаемые в школе:
Разложение левой части на

множители
Метод выделения полного квадрата
С применением формул

корней квадратного уравнения
С применением теоремы Виета
Графический способ

МОУ
Тулиновская средняя общеобразовательная школа

Способы решения квадратных уравненийИзучаемые в школе: Разложение левой части на множители Метод выделения полного квадрата С применением

Слайд 20Способы решения квадратных уравнений
Продвинутые способы:
Способ переброски
По свойству коэффициентов

С помощью циркуля и линейки
С помощью номограммы
Геометрический
МОУ
Тулиновская

средняя общеобразовательная школа

Способы решения квадратных уравненийПродвинутые способы: Способ переброски По свойству коэффициентов С помощью циркуля и линейки С помощью

Слайд 21Глейзер Г.И. История математики в школе. –
М., Просвещение,

1982.
Лиман М.М. Школьникам о математике и математиках. - М.,

Просвещение, 1981.
Пичугин Л.Ф. За страницами учебника алгебры. – М., Просвещение, 1990.
Пресман А.А. Решение квадратного уравнения с помощью циркуля и линейки. – М., квант, № 4/72, стр.34.
Ткачёва М.В. Домашняя математика. –М., Просвещение, 1994.
Энциклопедический словарь юного математика. – М., Педагогика, 1985.

Литература

МОУ
Тулиновская средняя общеобразовательная школа

Глейзер Г.И. История математики в школе. – М., Просвещение, 1982. Лиман М.М. Школьникам о математике и

Скачать презентацию

Теги

Разделы презентаций

Знакомьтесь, уравнение

Содержание

Слайды и текст этой презентации

Слайд 1Карл Фридрих Гаусс (1777-1855) немецкий математик, астроном, геодезист и физик,

иностранный член-корреспондент (1802) и иностранный почетный член (1824) Петербургской АНО,

Слайд 2Знакомьтесь, уравнение!Работу выполнила ученица 9-го класса Лёвина Дарья

Слайд 3Определение квадратного уравненияназывается квадратным уравнением где х – переменная,

а, b и c – некоторые числа, причем а

Слайд 4МОУ Тулиновская средняя общеобразовательная школаназывается дискриминантомВыражение

Слайд 5МОУ Тулиновская средняя общеобразовательная школаaх2 + вх + с =

0, а≠0D = в2-4асD < 0, тоD = 0, то

Слайд 6Исторические сведенияНеобходимость решать уравнения не только первой, но и второй

степени в древности была вызвана потребностью решать задачи, связанные с

Слайд 7Цель исследования:Выяснить, можно ли решать квадратное уравнение с помощью циркуля

и линейкиМОУ Тулиновская средняя общеобразовательная школа

Слайд 8ГипотезаПо данным действительным коэффициентам a, b, c уравнения ax2 +

bx + c = 0 (a ≠ 0) можно определить

Слайд 9Ход исследования:1. Изучив теоретический материал учебника и дополнительных источников информации

выяснить, способы решения квадратных уравнений с помощью циркуля и линейки.2.

Слайд 10Задача. По данным действительным коэффициентам

a, b, c уравнения ax2 + bx + c =

Слайд 11Ход решения задачиух(х1;0) (х2;0)FBKEAOC(0;1) S(;)(0;)МОУ Тулиновская средняя общеобразовательная школа

Слайд 12План нахождения корней квадратного уравнения с помощью циркуля и линейкиВ

системе координат построим точки

Слайд 13ух(х1;0)KEAO(0;1) S(0;)Радиус окружности больше ординаты центраВ этом случае окружность пересекает

ось Ох в точках В(х1;0) С(х2;0)(х2;0)СВМОУ Тулиновская

Слайд 14ух(х1;0)EAO(0;1) S(0;)Радиус окружности равен ординате центраВ этом случае уравнение имеет

равные действительные корни, абсцисса точки касания х1,2 =ВМОУ Тулиновская

Слайд 15ухEAO(0;1) S(0;)Радиус окружности меньше ординаты центраВ этом случае окружность не

имеет общих точек с осью Ох и уравнение имеет комплексные

Слайд 16Примеры:а) 2x2 + 3x + 1 = 0Определим координаты

точки центра окружности по формулам: x =y = Проведём окружность

Слайд 17Примеры:б) x2 - 5x + 6 = 0Определим координаты

точки центра окружности по формулам: x =y = Проведём окружность

Слайд 18Выводы1. Квадратные уравнения можно решать с помощью циркуля и линейки.2.

По данным действительным коэффициентам a, b, c уравнения ax2 +

Слайд 19Способы решения квадратных уравненийИзучаемые в школе: Разложение левой части на

множители Метод выделения полного квадрата С применением формул

Слайд 20Способы решения квадратных уравненийПродвинутые способы: Способ переброски По свойству коэффициентов

С помощью циркуля и линейки С помощью номограммы ГеометрическийМОУ Тулиновская

Слайд 21Глейзер Г.И. История математики в школе. – М., Просвещение,

1982. Лиман М.М. Школьникам о математике и математиках. - М.,

Похожие презентации

Обратная связь

Что такое TheSlide.ru?

иностранный член-корреспондент (1802) и иностранный почетный член (1824) Петербургской АН
О,

Слайд 2Знакомьтесь, уравнение!
Работу выполнила
ученица 9-го класса
Лёвина Дарья

Слайд 3Определение квадратного уравнения
называется квадратным уравнением
где х – переменная,

а, b и c – некоторые числа,
причем а

Слайд 4МОУ
Тулиновская средняя общеобразовательная школа
называется дискриминантом
Выражение

Слайд 5МОУ
Тулиновская средняя общеобразовательная школа
aх2 + вх + с =

0, а≠0
D = в2-4ас

D < 0, то
D = 0, то

Слайд 6Исторические сведения
Необходимость решать уравнения не только первой, но и второй

Слайд 7Цель исследования:
Выяснить, можно ли решать квадратное уравнение с помощью циркуля

и линейки
МОУ
Тулиновская средняя общеобразовательная школа

Слайд 8Гипотеза
По данным действительным коэффициентам a, b, c уравнения
ax2 +

Слайд 9Ход исследования:
1. Изучив теоретический материал учебника и дополнительных источников информации

выяснить, способы решения квадратных уравнений с помощью циркуля и линейки.
2.

Слайд 10Задача.
По данным действительным коэффициентам

a, b, c уравнения
ax2 + bx + c =

Слайд 11Ход решения задачи

у
х
(х1;0)
(х2;0)
F
B
K
E
A
O
C
(0;1)

S
(
;
)
(0;
)
МОУ
Тулиновская средняя общеобразовательная школа

Слайд 12План нахождения корней квадратного уравнения с помощью циркуля и линейки
В

системе координат построим

точки

Слайд 13
у
х
(х1;0)
K
E
A
O
(0;1)

S
(0;
)
Радиус окружности больше ординаты центра
В этом случае окружность пересекает

ось Ох в точках В(х1;0) С(х2;0)

(х2;0)
С
В
МОУ
Тулиновская

Слайд 14
у
х
(х1;0)
E
A
O
(0;1)

S
(0;
)
Радиус окружности равен ординате центра
В этом случае уравнение имеет

равные действительные корни, абсцисса точки касания х1,2 =
В
МОУ
Тулиновская

Слайд 15
у
х
E
A
O
(0;1)

S
(0;
)
Радиус окружности меньше ординаты центра
В этом случае окружность не

Слайд 16Примеры:

а) 2x2 + 3x + 1 = 0
Определим координаты

точки центра окружности по формулам:
x =
y =
Проведём окружность

Слайд 17Примеры:

б) x2 - 5x + 6 = 0
Определим координаты

точки центра окружности по формулам:
x =
y =
Проведём окружность

Слайд 18Выводы
1. Квадратные уравнения можно решать с помощью циркуля и линейки.
2.

По данным действительным коэффициентам a, b, c уравнения
ax2 +

Слайд 19Способы решения квадратных уравнений
Изучаемые в школе:
Разложение левой части на

множители
Метод выделения полного квадрата
С применением формул

Слайд 20Способы решения квадратных уравнений
Продвинутые способы:
Способ переброски
По свойству коэффициентов

С помощью циркуля и линейки
С помощью номограммы
Геометрический
МОУ
Тулиновская

Слайд 21Глейзер Г.И. История математики в школе. –
М., Просвещение,

1982.
Лиман М.М. Школьникам о математике и математиках. - М.,