Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Кластерный анализ
Содержание
- 1. Кластерный анализ
- 2. Актуальность Использование математических методов кластерного анализа в общеобразовательной школе, с их практическим подтверждением.
- 3. Цель исследованияИзучить основные математические модели кластерного анализа;Предложить
- 4. Математические методы и модели кластерного анализа.Предмет исследования
- 5. Гипотеза исследования
- 6. ЗАДАЧИ
- 7. Практическая значимость результатов заключается в том, что
- 8. Структура работы:
- 9. Кластерный анализ – это комплекс точных математических
- 10. Основные понятия
- 11. Аксиомы метрикиdij > 0 (неотрицательность расстояния)dij =
- 12. Применение
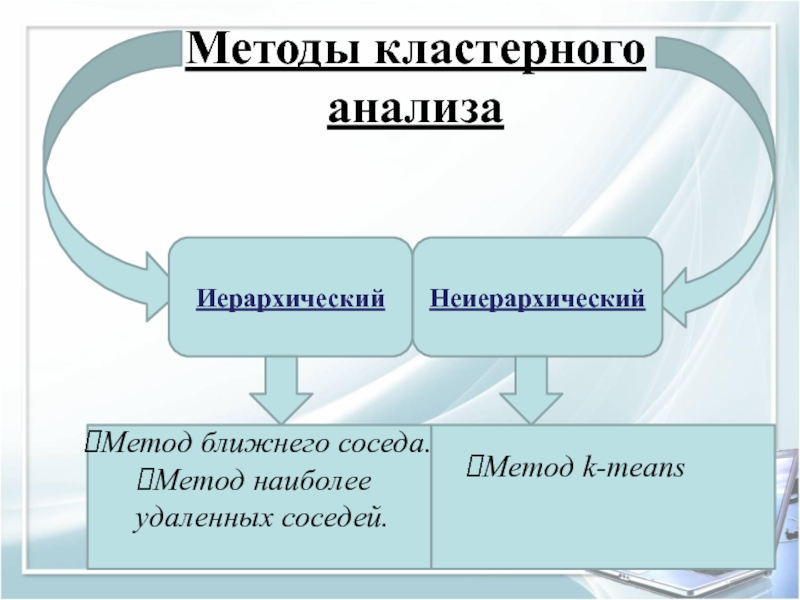
- 13. Методы кластерного анализаНеиерархическийИерархическийМетод ближнего соседа. Метод наиболее удаленных соседей.Метод k-means
- 14. Метод ближнего соседа или одиночная связь. Расстояние между двумя кластерами определяется
- 15. Метод полной связи (метод дальнего соседа)
- 16. Алгоритм k-meansАлгоритм k-means разделяет определенный набор данных
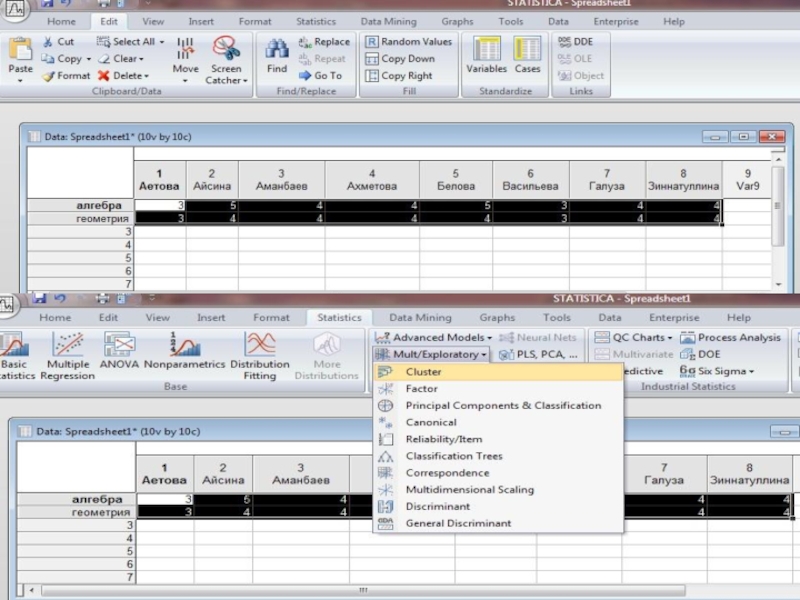
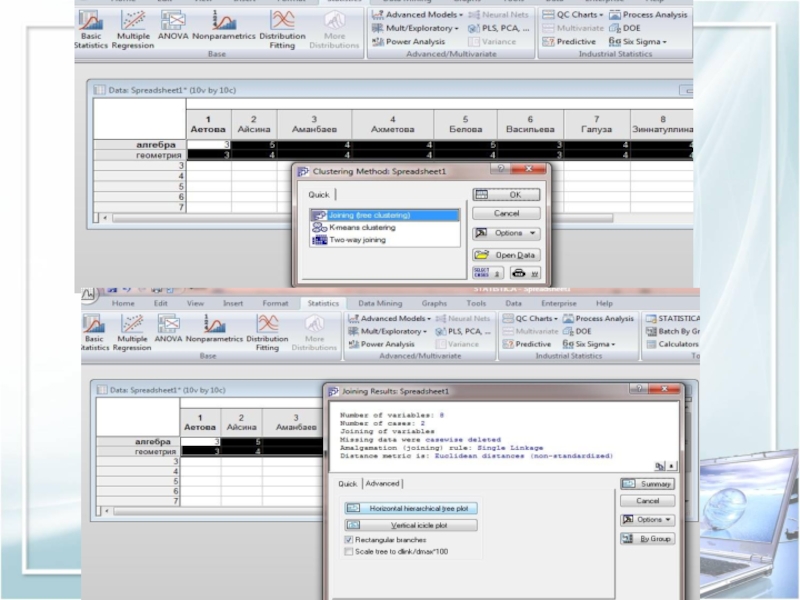
- 17. Пакет Statistica.
- 18. Слайд 18
- 19. Слайд 19
- 20. Слайд 20
- 21. Пример № 1.Эксперимент был направлен на практическое
- 22. Решение задач методом ближнего соседа. Рассматривается малая группа
- 23. Слайд 23
- 24. Слайд 24
- 25. Слайд 25
- 26. Слайд 26
- 27. Средние значения учащихся по кластерам
- 28. Вывод: Применив метод ближнего соседа, получено два
- 29. Решение задач методом дальнего соседа Необходимо
- 30. Слайд 30
- 31. Слайд 31
- 32. Вывод: Применив метод дальнего соседа получено два
- 33. Средние значения наблюдений по тестам в двух кластерах
- 34. Решение задач методом K-среднихНеобходимо рассмотреть малую
- 35. Слайд 35
- 36. Вывод: Методом K-means получено три кластера. В
- 37. Выводы
- 38. Скачать презентанцию
Актуальность Использование математических методов кластерного анализа в общеобразовательной школе, с их практическим подтверждением.
Слайды и текст этой презентации
Слайд 1Костанайский государственный педагогический институт
Естественно-математический факультет
Кафедра физико-математических и общетехнических дисциплин
Выполнила: Едрисова
А.С.
анализа»Слайд 2Актуальность
Использование математических методов кластерного анализа в общеобразовательной школе, с
их практическим подтверждением.
Слайд 3Цель исследования
Изучить основные математические модели кластерного анализа;
Предложить алгоритм и основные
этапы решения предлагаемых методов;
Обосновать использование математических методов кластерного анализа в
общеобразовательной школе;Изучить и обосновать использование математического пакета Statistica.
Использовать методы кластерного анализа для решения практических задач, а именно задач встречающихся в общеобразовательной школе.
Слайд 4
Математические методы и модели кластерного анализа.
Предмет исследования
Объект исследования
Использование и
применение методов кластерного анализа в общеобразовательных школах.
Слайд 7Практическая значимость результатов заключается в том, что полученные теоретические знания
применяются для исследования школьных коллективов, с целью составления кластеров по
успеваемости и психологической совместимости учащихся, с возможностью прогнозирования.Слайд 9Кластерный анализ – это комплекс точных математических методов, специализированных на
формировании "отдаленных" друг от друга групп «близких» между собой объектов
по информации о расстояниях или связях (мерах близости) между ними.Слайд 11Аксиомы метрики
dij > 0 (неотрицательность расстояния)
dij = dji (симметрия)
dij +
djk > dik (неравенство треугольника)
Если dij не равно 0, то
i не равно j (различимость нетождественных объектов)Если dij = 0, то i = j (неразличимость тождественных объектов)
Слайд 13Методы кластерного анализа
Неиерархический
Иерархический
Метод ближнего соседа.
Метод наиболее удаленных соседей.
Метод k-means
Слайд 14Метод ближнего соседа или одиночная связь.
Расстояние между двумя кластерами определяется расстоянием между двумя
наиболее близкими объектами (ближайшими соседями) в различных кластерах.
Слайд 15Метод полной связи
(метод дальнего соседа)
Метод дальнего соседа увеличивает число
компактных кластеров. Этот метод применим для решения задач с большим
количеством испытуемых.Слайд 16Алгоритм k-means
Алгоритм k-means разделяет определенный набор данных на заданное пользователем
число кластеров, k.
Это исторически один из самых важных алгоритмов
интеллектуального анализа данных.Слайд 21Пример № 1.
Эксперимент был направлен на практическое подтверждение теории кластерного
анализа.
Эксперимент проводился на базе ГУ «Школа-гимназия № 3 отдела образования
города Костаная. Экспериментом в общей сложности было охвачено 8 учеников 9 «В» класса.
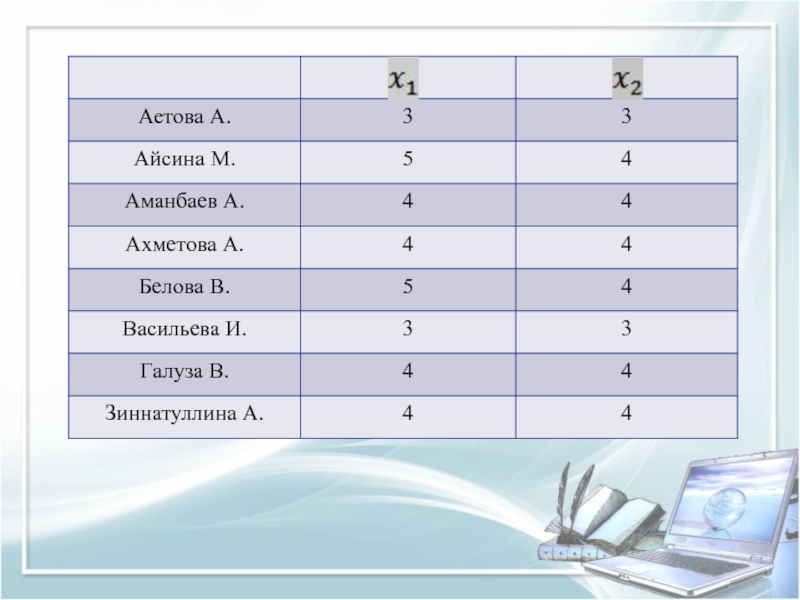
Слайд 22Решение задач методом ближнего соседа.
Рассматривается малая группа учеников из 8
человек. У которых - это характеристика оценок по
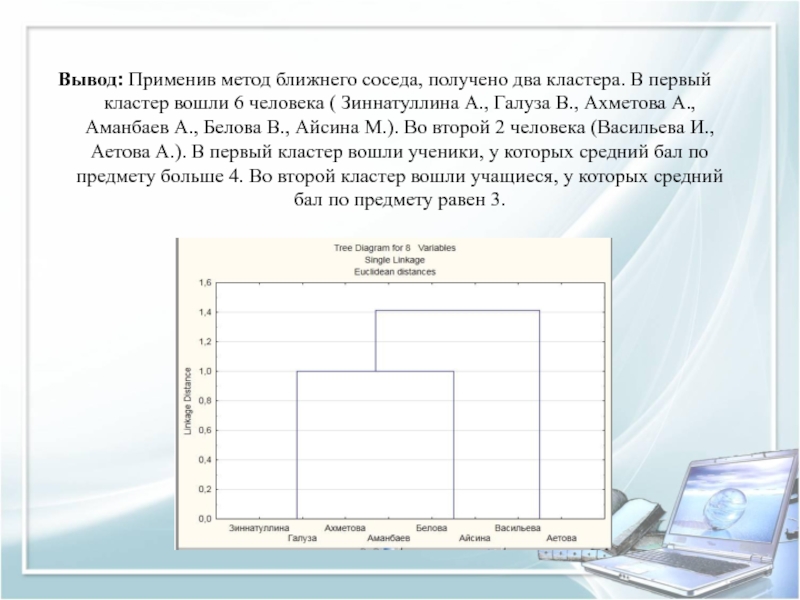
предмету алгебра, - это характеристика оценок учащихся по предмету геометрия. Данные приведены в таблице.Слайд 28Вывод: Применив метод ближнего соседа, получено два кластера. В первый
кластер вошли 6 человека ( Зиннатуллина А., Галуза В., Ахметова
А., Аманбаев А., Белова В., Айсина М.). Во второй 2 человека (Васильева И., Аетова А.). В первый кластер вошли ученики, у которых средний бал по предмету больше 4. Во второй кластер вошли учащиеся, у которых средний бал по предмету равен 3.Слайд 29
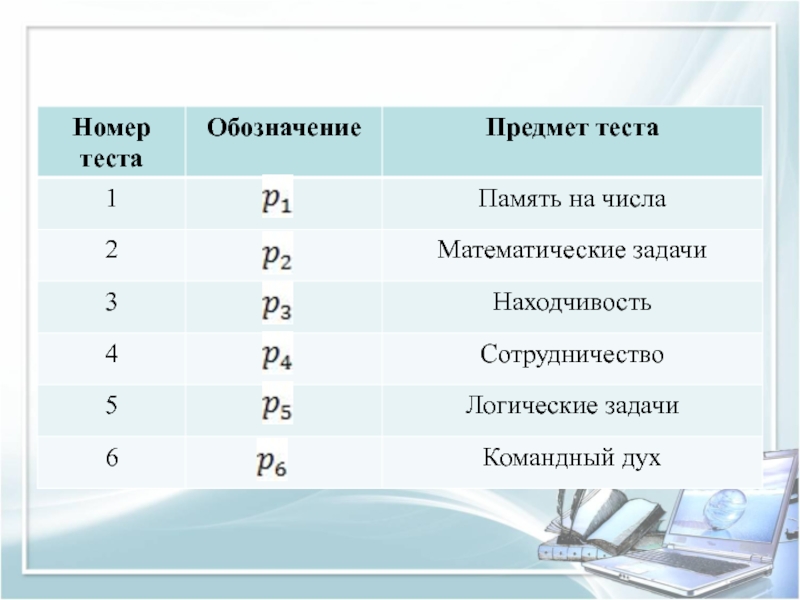
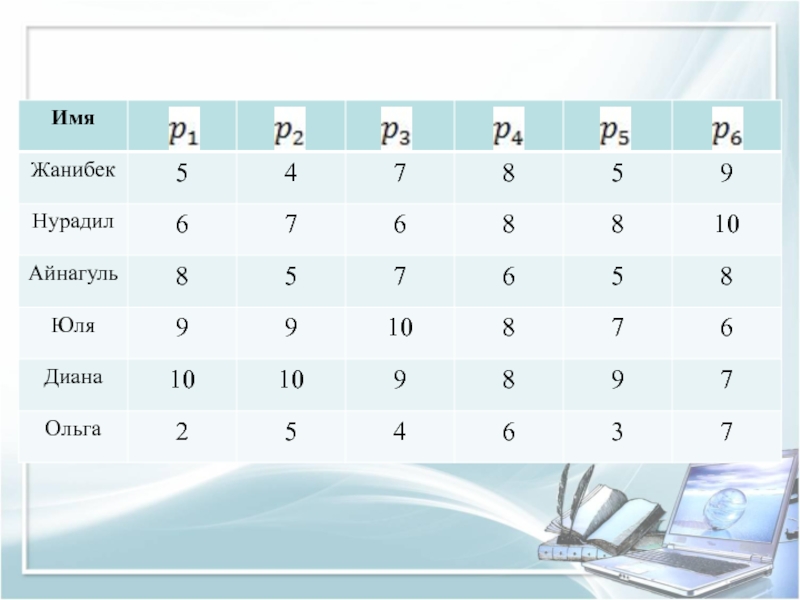
Решение задач методом дальнего соседа
Необходимо рассмотреть малую группу учащихся из
6 человек, которые прошли 6 различных теста.
Слайд 32Вывод: Применив метод дальнего соседа получено два кластера. В первый
кластер входят 2 студента (Диана и Юля), во второй 4
человека (Оля, Нурадил, Айнагуль, Жанибек).Слайд 34Решение задач методом
K-средних
Необходимо рассмотреть малую группу из 9 учеников.
Значения , ,
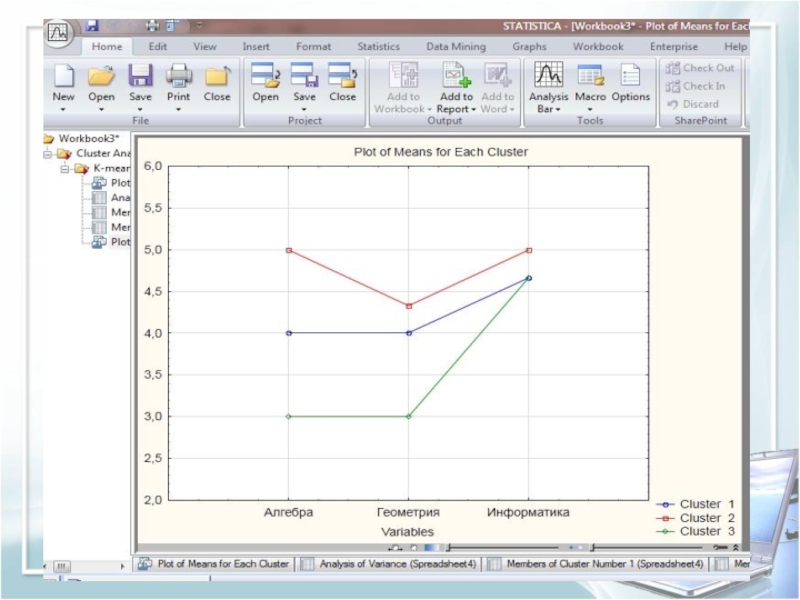
- оценки учащихся за I четверть по предметам: алгебра, геометрия, информатика.Слайд 36Вывод: Методом K-means получено три кластера. В первый кластер вошли
ученики: Аманбаев А., Ахметова А., Галуза В. У данных учеников
оценки по предметам « Алгебра» и « Геометрия» 4, по предмету информатика видно, что оценки лучше у всех членов трех кластеров.Во второй кластер вошли Айсина М., Белова В., Киколенко Ю. У данных учеников оценки по алгебре и информатике одинаковые, и выше чем по геометрии.
В третий кластер вошли Аетова А., Васильева И., Карпыков С. У них оценки по алгебре и геометрии низкие и равны оценке «3», но по информатике «4 и 5».