Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Мультимедийная презентация урока алгебры в 9 классе по теме "Решение неравенств"
Содержание
- 1. Мультимедийная презентация урока алгебры в 9 классе по теме "Решение неравенств"
- 2. План применения метода интервалов!
- 3. №1. Решите методом интервалов неравенства: б) №2.
- 4. Проверь своё решение№1. Решите методом интервалов неравенства:Вариант
- 5. Проверь своё решениеВариант 1.Вариант 2.№2. Найдите область определения функции:60 – – +Ответ:70 – – +Ответ:Решение.Решение.
- 6. Оценка самостоятельной работыЗа каждый верно выполненный пример
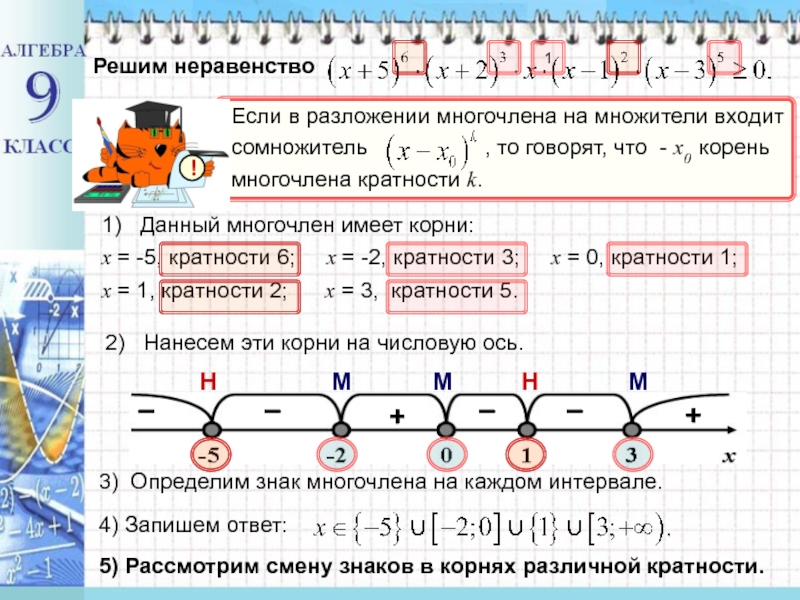
- 7. Решим неравенство1) Данный многочлен имеет корни:
- 8. Решите неравенство1 вариант:2 вариант:Сделайте выводы о смене знака на интервалах, в зависимости от степени кратности корня.
- 9. Обобщая ваши наблюдения, делаем выводы:
- 10. Решение рациональных неравенств Итак:
- 11. – Решим неравенство1) Найдем область определения неравенства:откуда2)
- 12. №389 (а, в), № 390 (в, г), №393(а), №394(а). Работа с учебником
- 13. Повторить §15 (глава II), №389 (б), №
- 14. Использованные источникиУчебник: Алгебра-9 класс, Ю.Н. Макарычев, Н.Г.
- 15. Слайд 15
- 16. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Применение метода интервалов для решения неравенств
МБОУ «Большекударинская СОШ»
Чернова Елена Алексеевна,
учитель математики.
Слайд 3
№1. Решите методом интервалов неравенства:
б)
№2. Найдите область определения
функции:
Вариант 1.
а)
Вариант 2.
б)
а)
Самостоятельная работа
!
Желаю удачи!
Слайд 4
Проверь своё решение
№1. Решите методом интервалов неравенства:
Вариант 1.
Вариант 2.
а)
а)
2,5
0,4
-3
-4
Ответ:
Ответ:
+
+
–
+
+
–
б)
б)
1/2
-3/2
+
+
–
Ответ:
1/3
-2/3
+
+
–
Ответ:
Слайд 5
Проверь своё решение
Вариант 1.
Вариант 2.
№2. Найдите область определения функции:
6
0
–
–
+
Ответ:
7
0
–
–
+
Ответ:
Решение.
Решение.
Слайд 6
Оценка самостоятельной работы
За каждый верно выполненный пример – поставьте 1
балл.
1 балл – удовлетворительно, «3».
2 балла – хорошо, «4».
3 балла – отлично, «5».
0 баллов – плохо, «2».
!
Слайд 7
Решим неравенство
1) Данный многочлен имеет корни:
x = -5,
кратности 6; x = -2, кратности 3;
x = 0, кратности 1;x = 1, кратности 2; x = 3, кратности 5.
2) Нанесем эти корни на числовую ось.
3) Определим знак многочлена на каждом интервале.
+
+
–
–
–
–
4) Запишем ответ:
5) Рассмотрим смену знаков в корнях различной кратности.
М
Н
Н
М
М
Слайд 8
Решите неравенство
1 вариант:
2 вариант:
Сделайте выводы о смене знака на интервалах,
в зависимости от степени кратности корня.
Слайд 11
–
Решим неравенство
1) Найдем область определения неравенства:
откуда
2) Сведем данное рациональное
неравенство к алгебраическому, умножив неравенство на квадрат знаменателя:
3) Находим
корни многочлена и определяем их кратность: х =1 (четная кратность), корни 3, -1, 0, 5, -2 (нечетная кратность).
4) Определим знак многочлена при х = 10, и расставим остальные знаки с учетом кратности корней.
Слайд 13Повторить §15 (глава II),
№389 (б), № 390 (б), №393(б),
№394(б).
Домашнее задание.
3. Что вам более всего удалось, какие моменты были выполнены
наиболее успешно?Рефлексия.
1.Что вы ожидали от работы на данном уроке? Сравните свои предварительные цели и реально достигнутые результаты.
2. Какие чувства и ощущения возникали у вас в ходе работы? Что оказалось для вас самым неожиданным?
4. Перечислите основные трудности, которые вы испытывали во время урока. Как вы их преодолевали?
Слайд 14Использованные источники
Учебник: Алгебра-9 класс, Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков,
С.Б. Суворова, М.: Просвещение, 2009.
2. Рурукин А.Н., Полякова С.А.,
Поурочные разработки по алгебре: 9 класс. – М.: ВАКО, 2010 – (В помощь школьному учителю).3. Для создания шаблона презентации использовалась картинка http://www.box-m.info/uploads/posts/2009-04/1238954029_1.jpg3. Для создания шаблона презентации использовалась картинка http://www.box-m.info/uploads/posts/2009-04/1238954029_1.jpg и шаблон с сайта http3. Для создания шаблона презентации использовалась картинка http://www.box-m.info/uploads/posts/2009-04/1238954029_1.jpg и шаблон с сайта http://3. Для создания шаблона презентации использовалась картинка http://www.box-m.info/uploads/posts/2009-04/1238954029_1.jpg и шаблон с сайта http://aida3. Для создания шаблона презентации использовалась картинка http://www.box-m.info/uploads/posts/2009-04/1238954029_1.jpg и шаблон с сайта http://aida.3. Для создания шаблона презентации использовалась картинка http://www.box-m.info/uploads/posts/2009-04/1238954029_1.jpg и шаблон с сайта http://aida.ucoz3. Для создания шаблона презентации использовалась картинка http://www.box-m.info/uploads/posts/2009-04/1238954029_1.jpg и шаблон с сайта http://aida.ucoz.3. Для создания шаблона презентации использовалась картинка http://www.box-m.info/uploads/posts/2009-04/1238954029_1.jpg и шаблон с сайта http://aida.ucoz.ru
4. Изображение кота http://s39.radikal.ru/i084/1008/34/683cd4886d3f.jpg