Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация для урока "Правильные многогранники или тела Платона"
Содержание
- 1. Презентация для урока "Правильные многогранники или тела Платона"
- 2. Содержание:ВведениеМногогранникиПравильные многогранникиИз истории правильных многогранников. Почему их называют телами Платона?Звездчатые многогранникиПлатонЗаключениеСписок используемой литературы
- 3. «Теория многогранников, в частности правильных многогранников,- одна из самых увлекательных глав геометрии.» Л. А. Люстернак.
- 4. Пирамида Хеопса
- 5. Многогранник называется правильным, если:Он выпуклыйВсе его грани-
- 6. Правильных многогранников всего пять:1-тетраэдр 2-гексаэдр 3-октаэдр 4-додекаэдр 5-икосаэдр
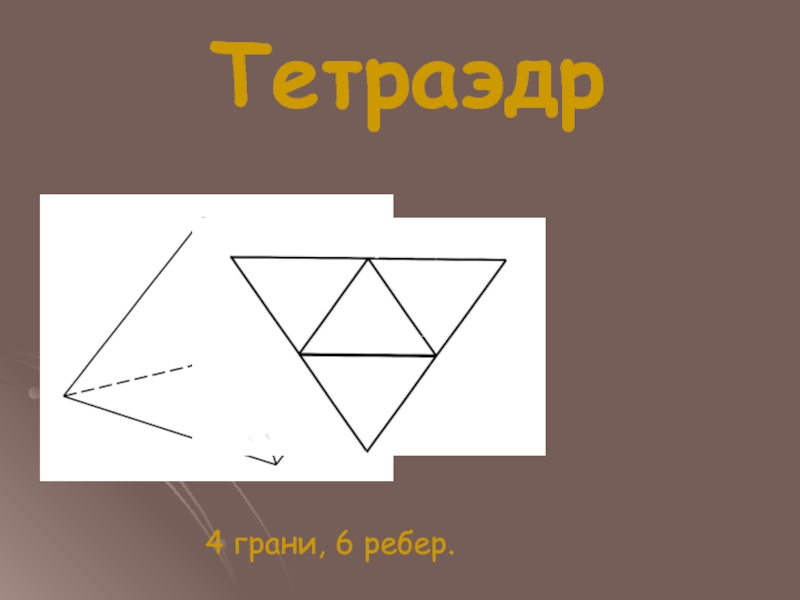
- 7. Тетраэдр
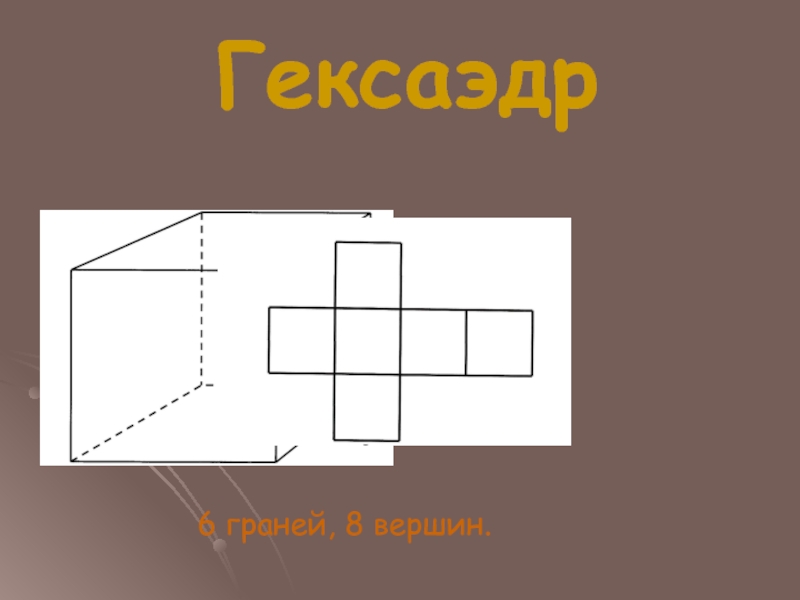
- 8. Гексаэдр
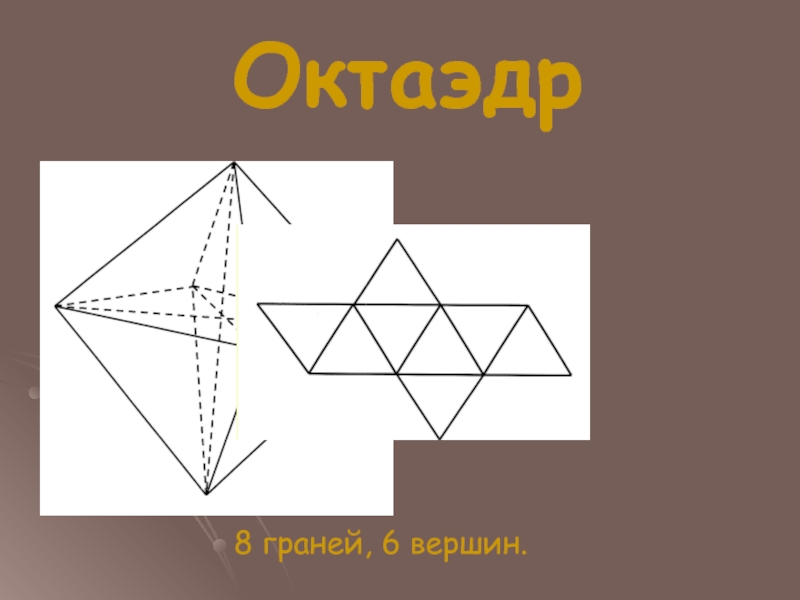
- 9. Октаэдр 8 граней, 6 вершин.
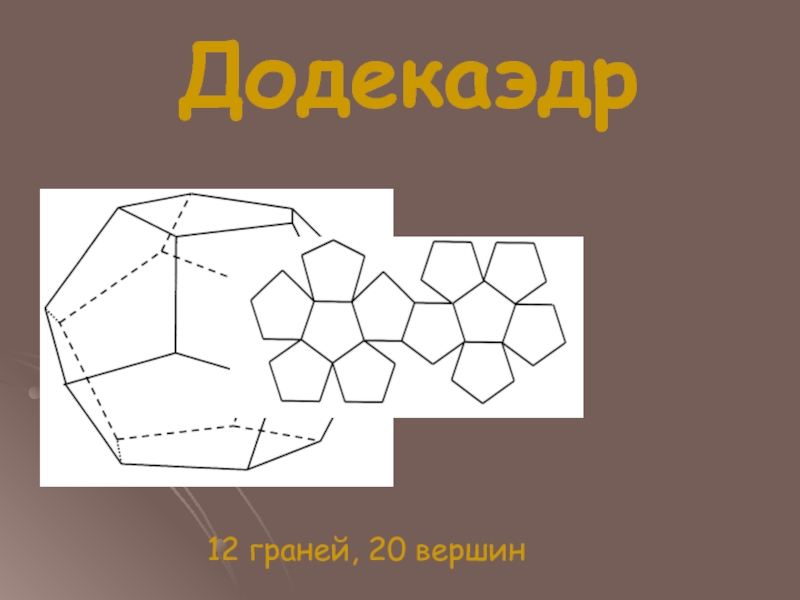
- 10. Додекаэдр 12 граней, 20 вершин
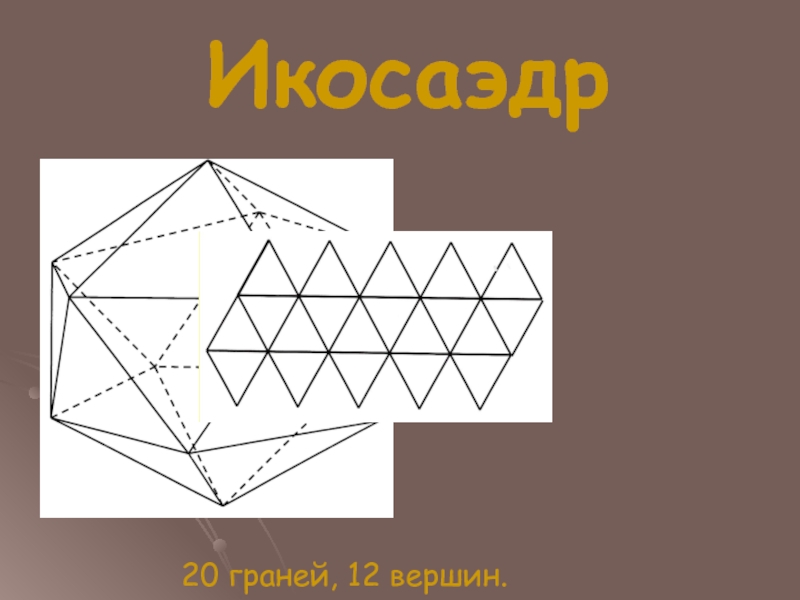
- 11. Икосаэдр 20 граней, 12 вершин.
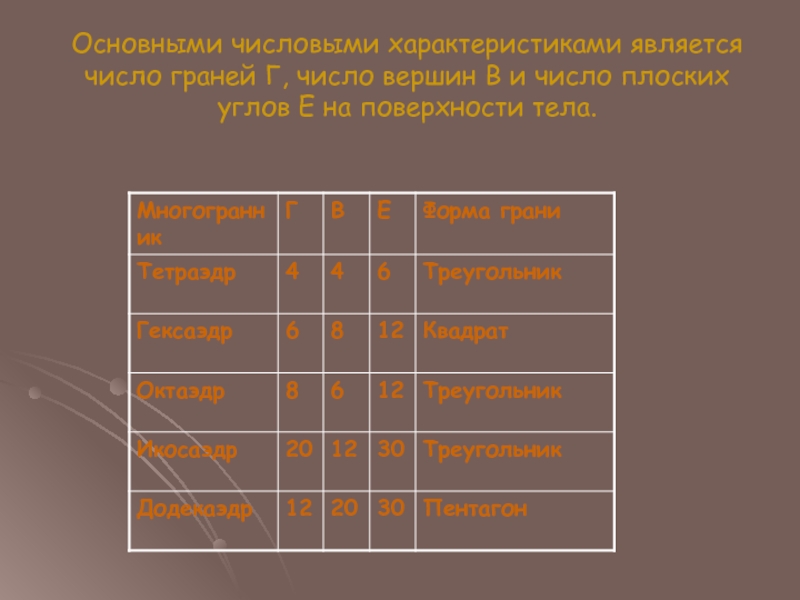
- 12. Основными числовыми характеристиками является число граней Г,
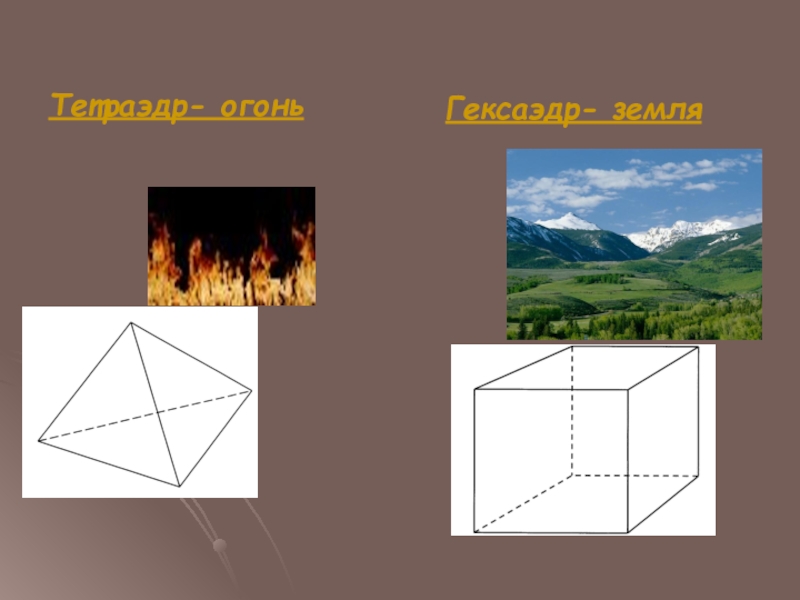
- 13. Тетраэдр- огоньГексаэдр- земля
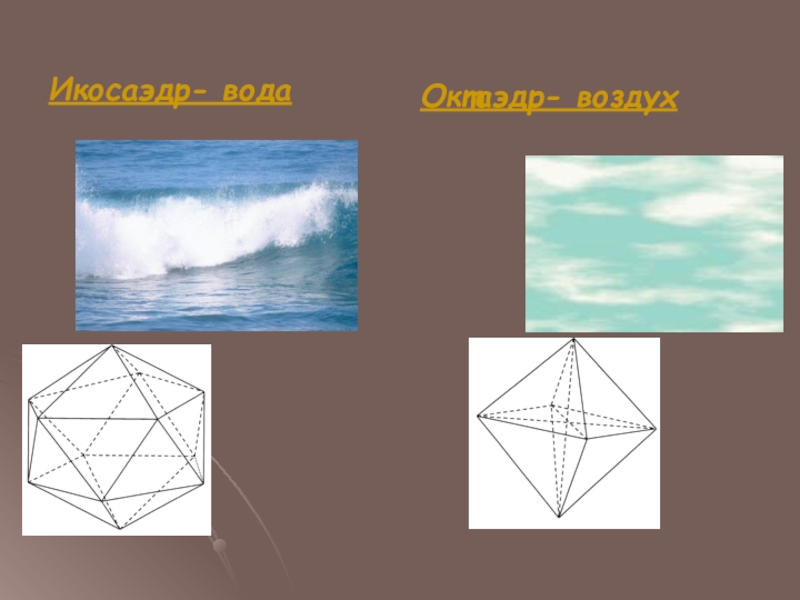
- 14. Икосаэдр- водаОктаэдр- воздух
- 15. Форму додекаэдра по мнению древних ученых имела
- 16. Леонардо Да Винчи проиллюстрировал изображениями правильных многогранников
- 17. В известной гравюре Альбрехта Дюрера «Меланхолия» на
- 18. Иоганн Кеплер в своей работе «Тайна мироздания»
- 19. Звездчатых многогранников всего 4:Малый звездчатый додекаэдрБольшой додекаэдрБольшой звездчатый додекаэдрБольшой икосаэдр
- 20. Звездчатые многогранники имеют декоративный вид, что позволяет их использовать в архитектуре.
- 21. Многие формы звездчатых многогранников подсказывает сама природа.Звездчатые многогранники в виде снежинок
- 22. Платон
- 23. О Н Е Ц К
- 24. Скачать презентанцию
Содержание:ВведениеМногогранникиПравильные многогранникиИз истории правильных многогранников. Почему их называют телами Платона?Звездчатые многогранникиПлатонЗаключениеСписок используемой литературы
Слайды и текст этой презентации
Слайд 2Содержание:
Введение
Многогранники
Правильные многогранники
Из истории правильных многогранников. Почему их называют телами Платона?
Звездчатые
многогранники
Слайд 3«Теория многогранников, в частности правильных многогранников,- одна из самых увлекательных
глав геометрии.»
Л. А. Люстернак.
Слайд 5Многогранник называется правильным, если:
Он выпуклый
Все его грани- равные друг другу
правильные многоугольники
В каждой его вершине сходится одинаковое число ребер
Все его
двугранные углы равны
Слайд 12Основными числовыми характеристиками является число граней Г, число вершин В
и число плоских углов Е на поверхности тела.
Слайд 15Форму додекаэдра по мнению древних ученых имела вселенная, т.е. они
считали, что мы живем внутри небесного свода, имеющего форму додекаэдра.
Сальвадор Дали «Тайная вечеря»
Слайд 16Леонардо Да Винчи проиллюстрировал изображениями правильных многогранников книгу монаха Луки
Пачоли «О божественной пропорции».
Леонардо Да Винчи «Правильный октаэдр и икосаэдр»
Слайд 17В известной гравюре Альбрехта Дюрера «Меланхолия» на переднем плане изображен
додекаэдр.
Альбрехт Дюрер «Меланхолия»
Слайд 18Иоганн Кеплер в своей работе «Тайна мироздания» вывел принцип которому
подчиняются формы и размеры орбит планет солнечной системы.
Космический кубок Кеплера
Слайд 19Звездчатых многогранников всего 4:
Малый звездчатый додекаэдр
Большой додекаэдр
Большой звездчатый додекаэдр
Большой икосаэдр
Слайд 20Звездчатые многогранники имеют декоративный вид, что позволяет их использовать в
архитектуре.
Слайд 21Многие формы звездчатых многогранников подсказывает сама природа.
Звездчатые многогранники в виде
снежинок
