Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Комбинаторные задачи. Комбинаторика
Содержание
- 1. Комбинаторные задачи. Комбинаторика
- 2. Слайд 2
- 3. граф-это геометрическая фигура, состоящая из точек (вершины графа) и линий, их соединяющих (рёбра графа).
- 4. Способы решения комбинаторных задач:Таблица вариантовДерево вариантовПравило умножения
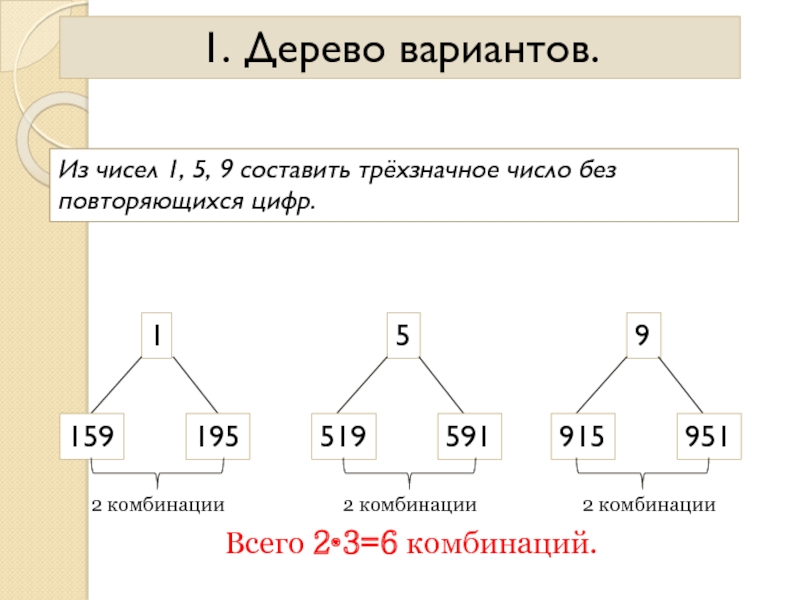
- 5. 1. Дерево вариантов.Из чисел 1, 5, 9
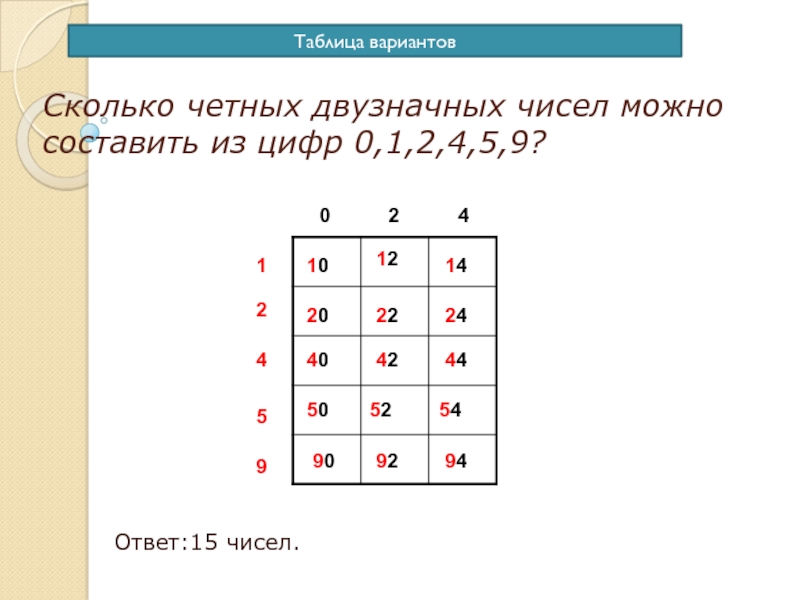
- 6. Сколько четных двузначных чисел можно составить из цифр 0,1,2,4,5,9?Ответ:15 чисел.12459024101412202224404244505254909294Таблица вариантов
- 7. На завтрак можно выбрать булочку, кекс, пряники
- 8. В коридоре висят три лампочки. Сколько имеется различных способов освещения коридора?
- 9. Первый способ - перебор вариантовОтвет: 8
- 10. Второй способ - дерево вариантовПервая лампочкаВторая лампочкаВторая
- 11. Третий способ - правило
- 12. Расписание уроков.В 9 классе в среду 6
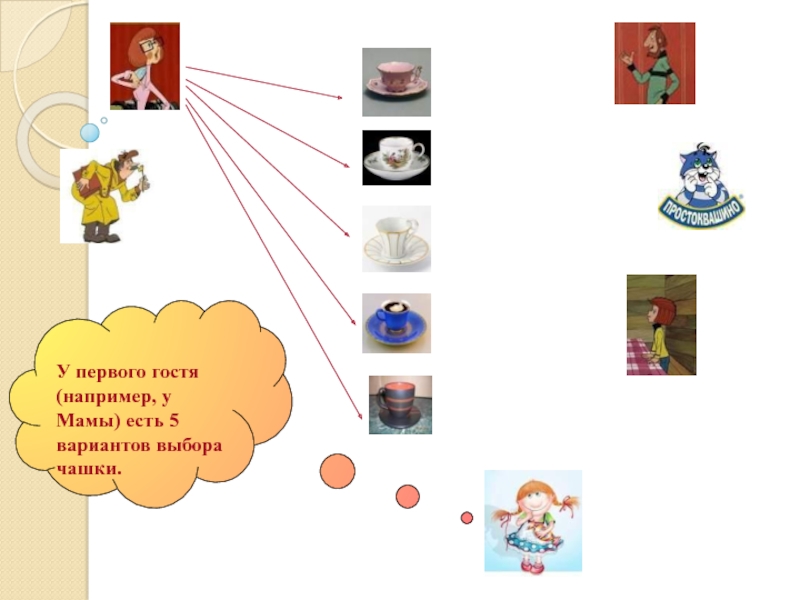
- 13. Дяде Федору для приема гостей мама и
- 14. У первого гостя (например, у Мамы) есть 5 вариантов выбора чашки.
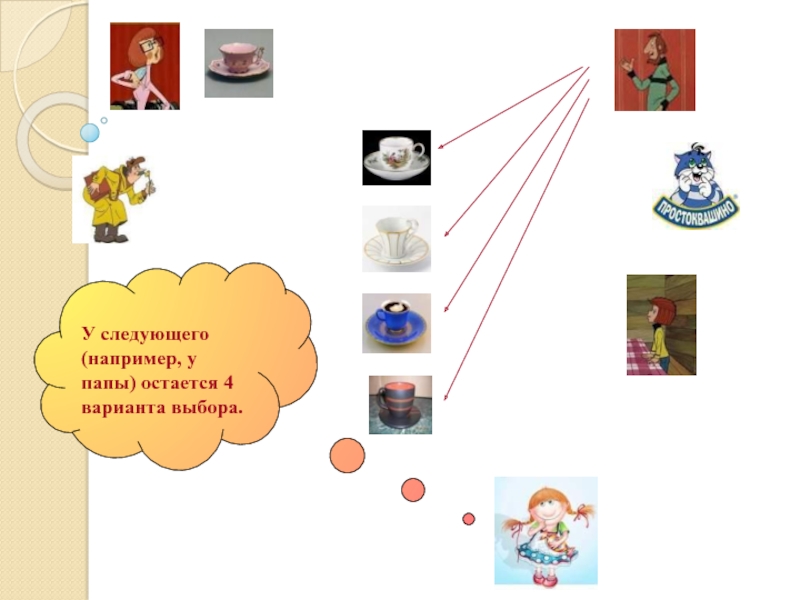
- 15. У следующего (например, у папы) остается 4 варианта выбора.
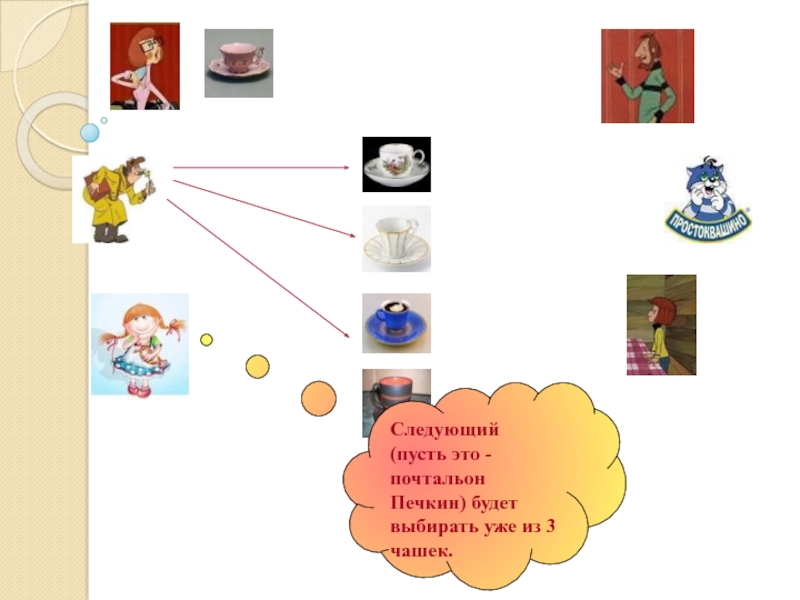
- 16. Следующий (пусть это - почтальон Печкин) будет выбирать уже из 3 чашек.
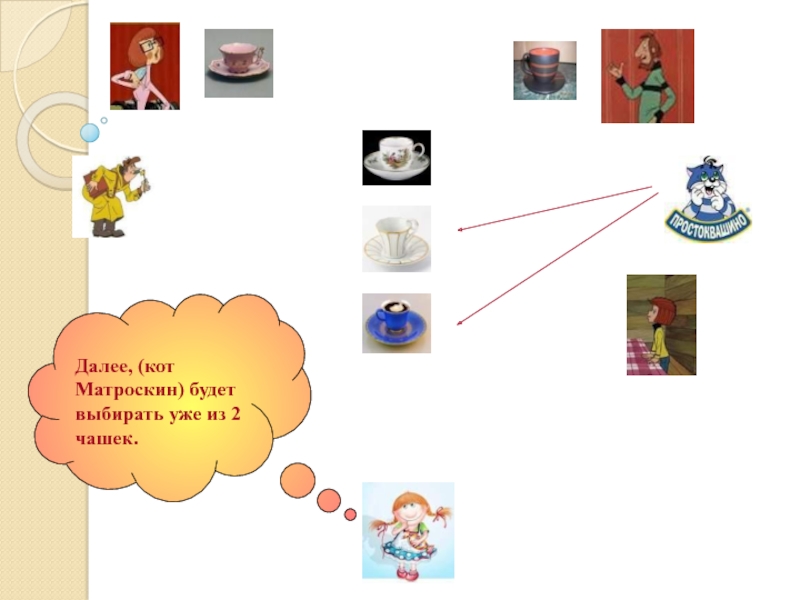
- 17. Далее, (кот Матроскин) будет выбирать уже из 2 чашек.
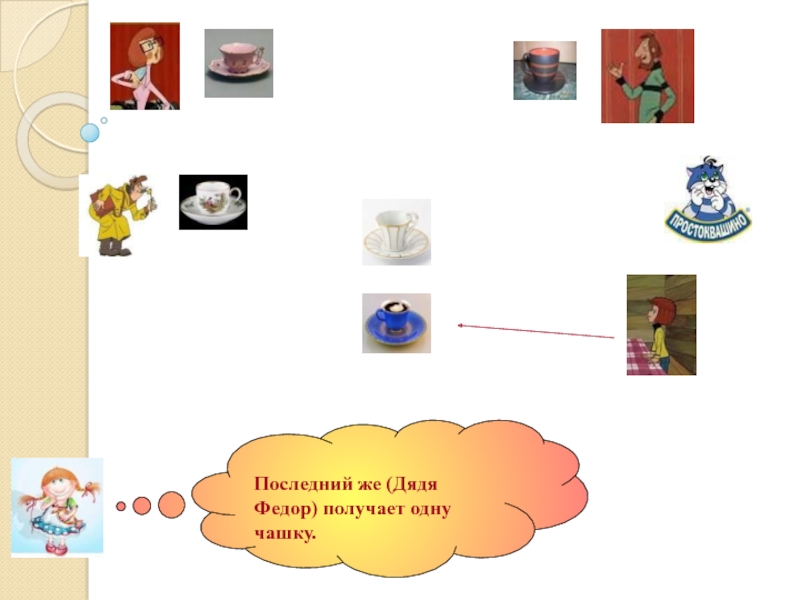
- 18. Последний же (Дядя Федор) получает одну чашку.
- 19. Получили, что каждому выбору чашки мамой соответствует
- 20. Заметим, что 5 • 4 • 3
- 21. Семейный ужин.Пример В семье 6 человек, а
- 22. 3. « Эн факториал»-n!.1•2•3•4•5•6=720Определение. Произведение подряд идущих
- 23. Закончите предложение и ответьте на вопросЧему…?Где…?Зачем…?Как…?
- 24. Спасибо за урок!
- 25. Скачать презентанцию
граф-это геометрическая фигура, состоящая из точек (вершины графа) и линий, их соединяющих (рёбра графа).
Слайды и текст этой презентации
Слайд 3граф-это геометрическая фигура, состоящая из точек (вершины графа) и линий,
их соединяющих (рёбра графа).
Слайд 51. Дерево вариантов.
Из чисел 1, 5, 9 составить трёхзначное число
без повторяющихся цифр.
1
159
195
5
9
519
591
915
951
2 комбинации
2 комбинации
2 комбинации
Всего 2•3=6
комбинаций. 
Слайд 6Сколько четных двузначных чисел можно составить из цифр 0,1,2,4,5,9?
Ответ:15 чисел.
1
2
4
5
9
0
2
4
10
14
12
20
22
24
40
42
44
50
52
54
90
92
94
Таблица
вариантов
Слайд 7На завтрак можно выбрать булочку, кекс, пряники или печенье, запить
можно чаем, соком или кефиром. Сколько вариантов завтрака есть?
х/б
изд.
напитки
булочка
кекс
пряники
печенье
чай
сок
кефир
чай
чай
чай
чай
кефир
сок
сок
сок
сок
кефир
кефир
кефир
булочка
булочка
булочка
кекс
кекс
кекс
пряники
пряники
пряники
печенье
печенье
печенье
Выбор напитка-
испытание АВыбор хл./бул. изделия.- испытание В
Испытание А имеет 3 варианта (исхода), а испытание В-4, всего вариантов
независимых испытаний А и В 3•4=12.
Для того, чтобы найти число
всех возможных исходов
(вариантов) независимого
проведения двух испытаний
А и В, надо перемножить число
всех исходов испытания А на
число всех исходов испытания В
Правило умножения.
Слайд 10Второй способ - дерево вариантов
Первая лампочка
Вторая лампочка
Вторая лампочка
Третья
лампочка
Третья
лампочка
Третья
лампочка
Третья
лампочка
+
+
+
+ + --
+
+
+
---
---
---
---
---
---
---
+
+
+
+ -- +
+ -- --
+
-- +
+-- + --
-- -- +
-- -- --
Ответ: 8
Слайд 11 Третий способ - правило умножения
Для каждой лампочки
возможны два исхода (гореть или не гореть), а лампочек три,
значит2×2×2=8
Ответ:8.
Слайд 12Расписание уроков.
В 9 классе в среду 6 уроков: геометрия, литература,
русский язык, английский язык, биология и физкультура. Сколько вариантов расписания
можно составить?Расставляем предметы по порядку
Геометрия
6
Литература
5
Русский язык
4
Английский язык
3
Биология
2
1
Физкультура
Всего вариантов расписания
1•2•3•4•5•6=
720
Слайд 13Дяде Федору для приема гостей мама и папа подарили 5
разных чашек. Сколькими способами можно разделить чашки между гостями?
В
гости к Дяде Федору пришли папа, мама, кот Матроскин и почтальон Печкин.
Слайд 19
Получили, что каждому выбору чашки мамой соответствует 4 возможных выбора
папы, т.е. всего 5 • 4 способов. После того, как
папа выбрал чашку, у Печкина есть 3 варианта выбора, у Матроскина – 2, у Дяди Федора – 1, т.е. всего5 • 4 • 3 • 2 • 1 способов
Слайд 20Заметим, что 5 • 4 • 3 • 2 •
1 – это произведение всех натуральных чисел от 1 до
5. такие произведения записывают короче5 • 4 • 3 • 2 • 1 = 5!
(читают «пять факториал»)
Слайд 21Семейный ужин.
Пример
В семье 6 человек, а за столом в
кухне 6 стульев. Было решено каждый вечер перед ужином рассаживаться
на эти 6 стульев по-новому. Сколько дней члены семьи смогут делатьэто без повторений?
№1
№2
№3
№4
№5
№6
6
5
4
3
2
1
6•5•4•3•2•1=
720дн.
-почти 2 года
Слайд 223. « Эн факториал»-n!.
1•2•3•4•5•6=720
Определение.
Произведение подряд идущих первых n
натуральных чисел
обозначают n! и называют
«эн факториал»: n!=1•2•3•…•(n-1)•n.
2!=
1•2=
2
3!=
1•2•3=
6
4!=
1•2•3•4=
24
5!=
1•2•3•4•5=
6!=
120
1•2•3•4•5•6=
720
7!=
1•2•3•4•5•6•7=
5040
n!=(n-1)!•n
Удобная формула!!!
