Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
История возникновения числа
Содержание
- 1. История возникновения числа
- 2. Система счисления: позиционные непозиционные
- 3. Самая простая система счисления была еще у
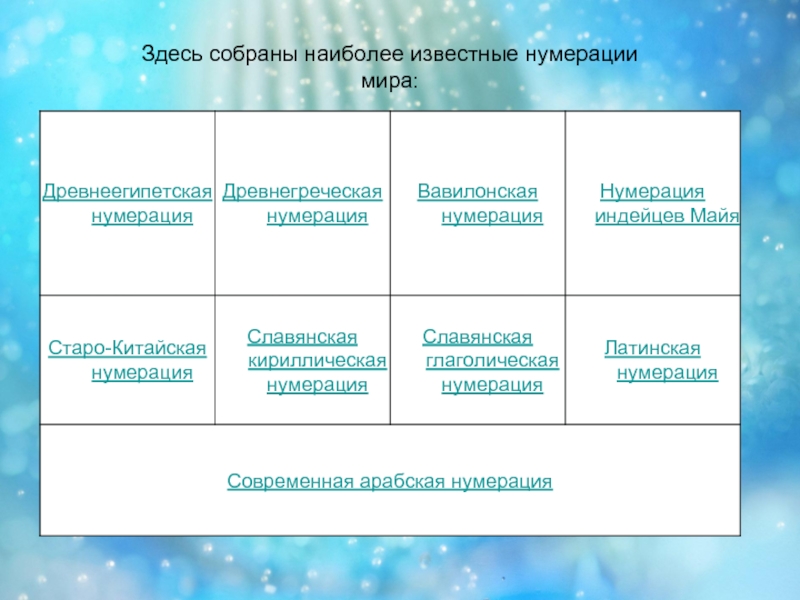
- 4. Здесь собраны наиболее известные нумерации мира:
- 5. Первый тип: XXXV = 10+10+10+5 = 35;
- 6. Аддитивная система счисления 1 234…91011 ИА ведь
- 7. Например 0, 1, 2, 3, 4, 5,
- 8. Египетская нумерация 1 Как и большинство людей
- 9. 100 000. Это головастик. Обычный лягушачий головастик. 1 000 000.
- 10. В древнейшее время в Греции была распространена
- 11. Примерно в третьем веке до нашей эры
- 12. Вавилонская нумерация В вавилонской поместной нумерации ту
- 13. Вавилонский способ обозначения чисел больше 60 .Цифры
- 14. Нумерация индейцев Майя Сначала эта нумерация обслуживала
- 15. Записывались цифры числа в столбик, начиная со
- 16. Славянская кириллическая нумерация Интереснее всего записывались числа
- 17. Китайская нумерация 12345 6789Записывались цифры числа начиная с больших значений и заканчивая меньшими
- 18. 101001000- 1 000; - 548 Такая запись числа
- 19. Самая простая система счисления В этой системе
- 20. Латинская (Римская) нумерация Возникла эта нумерация в
- 21. Прежде знак M изображался знаком Ф, потому
- 22. Новая или арабская нумерация В ней цифры
- 23. Спасибо за внимание!
- 24. Скачать презентанцию
Слайды и текст этой презентации
Слайд 3Самая простая система счисления была еще у древних людей.
Аддитивная система
счисления.
системах счисленияСлайд 5Первый тип:
XXXV = 10+10+10+5 = 35; CCXIX = 100+100+10-1+10
= 219;
Второй тип:
Система счисления:
(иероглифы по порядку: 2, 1000,
4, 100, 2, 10, 5)
Здесь дважды использован иероглиф "2", и в каждом случае он принимал разные значения "2000" и "20".2 1000 + 4 100+2 10+5 = 2425
Слайд 6Аддитивная система счисления
1
2
3
4
…
9
10
11
И
А ведь всего-то это 1457
2026.Удобств для счета, как мы видим ни каких. Такой
системой счисления пользовались Египтяне пользовались Египтяне, Ацтеки, племена Майя.Слайд 7Например 0, 1, 2, 3, 4, 5, 6, 7, 8,
9, 10 11, 12, …, 99, 100, 101 …
Запись числа
1999 означает, что 1 1000 + 9 100 + 9 10 + 9.Для того, чтобы "собрать" такое число используется умножение
(multiplication англ.), из-за чего систему и назвали "мультипликативной".
Такие системы счисления были только у народов с очень хорошо
развитой математикой. По сей день мы используем только такую систему
счисления.
Мультипликативная система счисления.
Слайд 8Египетская нумерация
1 Как и большинство людей для счета небольшого
количества
предметов Египтяне использовали палочки.
10. Такими путами египтяне связывали
коров Если нужно изобразить несколько десятков,
то иероглиф повторяли нужное количество раз.
Если палочек нужно изобразить несколько,
то их изображали в два ряда
100. Это мерная веревка, которой
измеряли земельные участки после разлива Нила.
1 000. Египтяне присвоили такое значение изображению этого
цветка.
10 000. "В больших числах будь внимателен!" –
говорит поднятый вверх указательный палец.
Слайд 9100 000. Это головастик. Обычный лягушачий головастик.
1 000 000. Увидев такое число
обычный человек очень
удивится и возденет руки к небу.
Это
и изображает этот иероглиф 10 000 000. Египтяне поклонялись Амону Ра,
богу Солнца, и, наверное,
поэтому самое большое свое число они
изобразили в виде восходящего солнца
- 1207,
- 1 023 029
Слайд 10В древнейшее время в Греции была распространена так называемая Аттическая
нумерация. В этой нумерации числа 1, 2, 3, 4 изображались
соответствующим количествомвертикальных полосок: , , , . Число 5
записывалось знаком (древнее начертание буквы "Пи", с которой начиналось слово "пять" - "пенте". Числа 6, 7, 8, 9 обозначались сочетаниями этих знаков:
Число 10 обозначалось - заглавной "Дельта" от слова "дека" - "десять". Числа 100, 1 000 и 10 000 обозначались H, X, M. Числа 50, 500, 5 000 обозначались комбинациями чисел 5 и 10, 5 и 100, 5 и 1 000,.
Древняя греческая нумерация
Слайд 11Примерно в третьем веке до нашей эры аттическая нумерация в
Греции была вытеснена другой, так называемой "Ионийской" системой. В ней
числа 1 - 9 обозначаются первыми буквами греческого алфавита:числа 10, 20, … 90 изображались следующими девятью буквами :ѓ
числа 100, 200, … 900 последними девятью буквами:
Для обозначения тысяч и десятков тысяч пользовались теми же цифрами, но только с добавлением особого значка '. Любая буква с этим значком сразу же становилась в тысячу раз больше.
Для отличия цифр и букв писали черточки над цифрами.
Слайд 12Вавилонская нумерация
В вавилонской поместной нумерации ту роль, которую у
нас играет число10, играет число 60, и потому эту нумерацию
называют шестидесятиричной. Числа менее 60 обозначались с помощью двух знаков:для единицы, и
Эти знаки повторялись нужное число раз, например
для десятка.
-3
-20
-32
а это число 59.
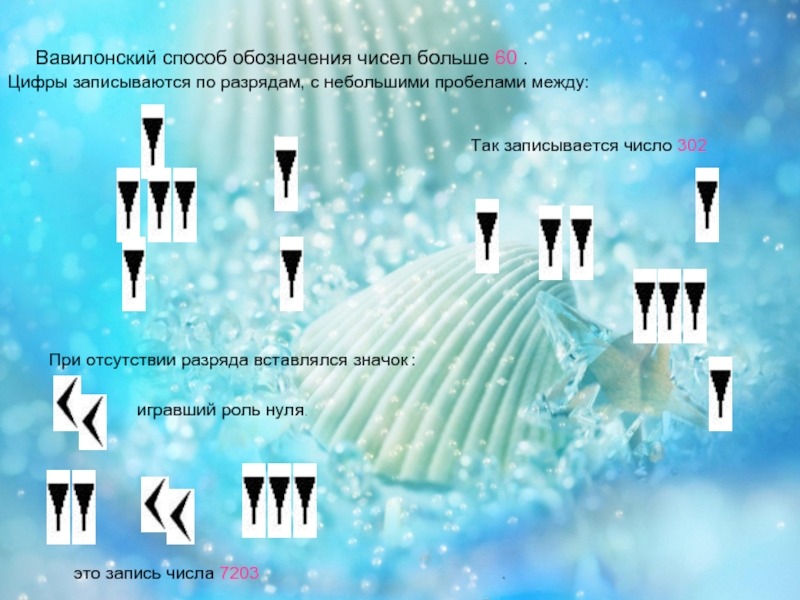
Слайд 13Вавилонский способ обозначения чисел больше 60 .
Цифры записываются по разрядам,
с небольшими пробелами между:
Так записывается число 302
При отсутствии разряда
вставлялся значок :игравший роль нуля.
это запись числа 7203
Слайд 14Нумерация индейцев Майя
Сначала эта нумерация обслуживала пятеричную систему счисления,
а потом ее приспособили для двадцатеричной.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
0 или 20
Слайд 15 Записывались цифры числа в столбик, начиная со знаков
затем
знаки
, а потом
больших значений и заканчивая меньшими.
,
59
16
23
20+20+5+5+5+1+1+1+1
= 59; 5+5+5+1 = 16; 20+1+1+1 = 23Слайд 16Славянская кириллическая нумерация
Интереснее всего записывались числа
второго десятка:
Читаем дословно
"четырнадцать" - "четыре на десять". Как слышим, так и пишем:
не 10+4, а 4+10, - четыре на десять. И так для всех чисел от 11 до 19.
Таким образом у славян мы прослеживаем десятеричную систему счисления.
Запись числа, использованная славянами аддитивная, то есть в ней используется только
сложение:
= 800+60+3
Тысяща - 1 000, Леон - 10 000, Одр - 100 000, Вран (ворон) - 1 000 000, Колода - 10 000 000,
Тьма - 100 000 000.
Слайд 17Китайская нумерация
1
2
3
4
5
6
7
8
9
Записывались цифры числа начиная с больших
значений и заканчивая меньшими
Слайд 1810
100
1000
- 1 000;
- 548
Такая запись числа мультипликативная, то есть
в ней используется умножение:
1 1 000 и 5 100+4 10+8
Слайд 19Самая простая система счисления
В этой системе счисления для записи
чисел используется только одна цифра. Ее можно изобразить в виде
палочки , кружочка , или любой другой фигуры. Числа будут записываться примерно так:Слайд 20Латинская (Римская) нумерация
Возникла эта нумерация в древнем Риме. Использовалась
она для аддитивной алфавитной
системы счисления
Слайд 21Прежде знак M изображался знаком Ф, потому то 500 и
стал изображать знак D как "половина" Ф. Так же построена
и пары L и C, X и V.Записывались цифры числа начиная с больших значений и заканчивая меньшими, слева направо.
Если цифра с меньшим значением записывалась перед цифрой с большим значением, то происходило ее вычитание.
CCXXXVII = 100+100+10+10+10+5+1+1 = 237НоXXXIX = 10+10+10-1+10 = 39
Есть правило, по которому нельзя записывать подряд 4 одинаковых цифры,
такая комбинация заменяется комбинацией с правилом вычитания, например:
XXXX = XC (50-10)
IIII = IV (5-1)
CCCC = CD (500-100)
Слайд 22Новая или арабская нумерация
В ней цифры имели вид
начальных букв соответствующих числительных
на древнеиндийском языке - санскрите, использующем
алфавит "Деванагари".Первоначально этими знаками представлялись числа 1, 2, 3, … 9, 10, 20, 30, …,
90, 100, 1000; с их помощью записывались другие числа.