Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Полезные теоремы Чевы и Менелая
Содержание
- 1. Полезные теоремы Чевы и Менелая
- 2. Теорема Менелая.Пусть дан треугольник ABC и точки
- 3. Доказательство:Необходимость. Пусть прямая l пересекает прямые AB, BC, AC
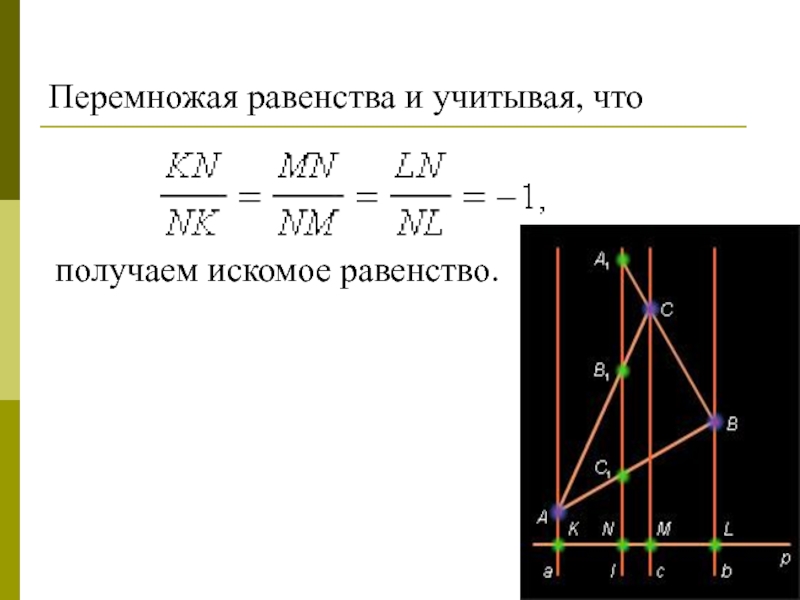
- 4. Перемножая равенства и учитывая, что получаем искомое равенство.
- 5. Достаточность. Пусть дан треугольник ABC, точки
- 6. Действительно, если доказать противное, а именно, что
- 7. По условию имеем: с другой стороны, в
- 8. Теорема Чевы Пусть на сторонах треугольника ABC
- 9. Доказательство:
- 10. Обобщенная теорема Чевы. Пусть прямые a, b,
- 11. Слайд 11
- 12. Доказательство:Для случая параллельных прямых (слева на рисунке ) из теоремы Фалеса имеем соотношение
- 13. Перемножая левые и правые части равенств, получаем
- 14. Если λ > 0, то B' и B1 делят
- 15. Отсюда следует из подобия треугольников AA1C и
- 16. Перемножая соответственно левые и правые части равенств,
- 17. Следствие 14.1. Медианы треугольника пересекаются в одной точке. В этом случае
- 18. Следствие 14.2. Биссектрисы треугольника пересекаются в одной точке.Доказательство:Действительно из свойства биссектрис можно записать следующие равенства:
- 19. Следствие 14.3. Прямые, соединяющие вершины треугольника с точками
- 20. Следствие 14.4. Высоты треугольника пересекаются в одной точке.
- 21. Слайд 21
- 22. Пусть треугольник ABC тупоугольный (см. рис. ). Применим
- 23. Скачать презентанцию
Теорема Менелая.Пусть дан треугольник ABC и точки на, соответственно, прямых AB, AC и BC. Точки лежат на одной прямой тогда и только тогда, когда выполняется равенство
Слайды и текст этой презентации
Слайд 3Доказательство:
Необходимость. Пусть прямая l пересекает прямые AB, BC, AC соответственно в точках
C1, A1 и B1 (см. рис.). Проведем произвольную прямую P, пересекающую
прямую l в точке N, а через точки A, B и C соответственно прямые a, b и c, параллельные прямой l и пересекающие p в точках K, L, M. По теореме о пропорциональных отрезках:
Слайд 5Достаточность.
Пусть дан треугольник ABC, точки
и пусть выполнено
необходимое условие. Докажем, что точки A1, B1 и C1 лежат на
одной прямой. Проведем прямую через заданные две точки A1 и B1. Эта прямая пересекает прямую AB в некоторой точке C'.
Слайд 6Действительно, если доказать противное, а именно, что прямая A1B1'║(AB), то
из подобия треугольников CA1B1 и CBA следует, что
С учетом
необходимого условия получим, что Но такой точки не может существовать, и мы пришли к противоречию.
Слайд 7По условию имеем:
с другой стороны, в силу необходимого условия
справедливо равенство
Откуда получаем
и приходим к выводу, как и
в случае доказательства обобщенной теоремы Чевы, что точки C1 и C' совпадают. 
Слайд 8Теорема Чевы
Пусть на сторонах треугольника ABC выбраны точки
Отрезки
,
и
пересекаются в одной точке тогда и только тогда, когда
выполняется равенство:
Слайд 10
Обобщенная теорема Чевы. Пусть прямые a, b, c проходят через
вершины A, B, C треугольника ABC и пересекает прямые BC,
CA, AB в точках соответственно (см. рис.). Тогда прямые a, b, c пересекаются в одной точке или параллельны тогда и только тогда, когда имеет место равенство
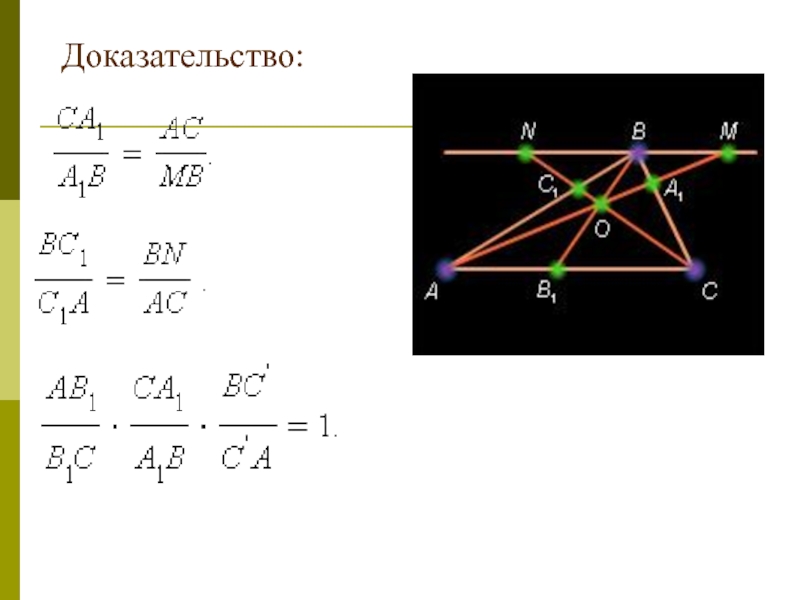
Слайд 12Доказательство:
Для случая параллельных прямых (слева на рисунке ) из теоремы Фалеса
имеем соотношение
Слайд 13Перемножая левые и правые части равенств, получаем искомое равенство.
Обратно,
пусть выполнено необходимое условие и при этом
Тогда, проведя через
вершину B прямую найдем точку B' ее пересечения с прямой AC. Как и в случае доказательства первой теоремы, получим
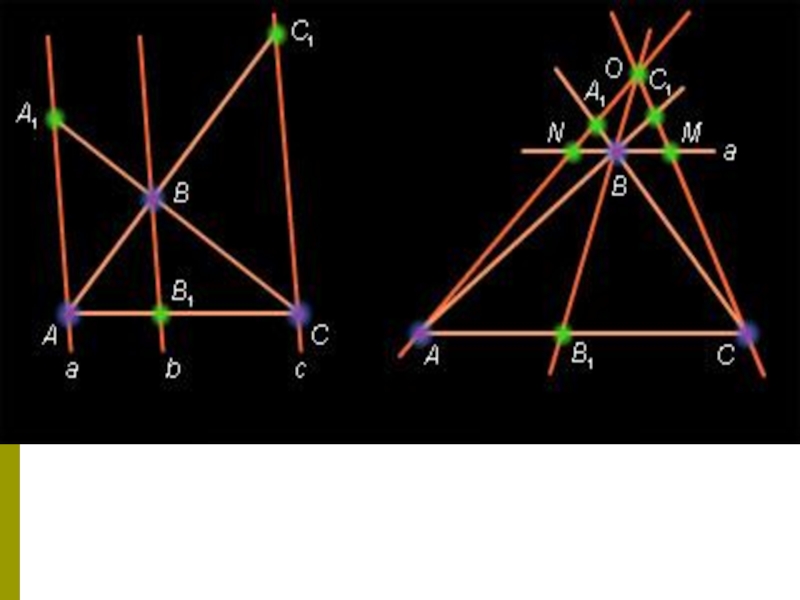
Слайд 14Если λ > 0, то B' и B1 делят отрезок AC в
одном отношении и, следовательно, совпадают. Если λ
и B1 лежат вне отрезка AC по одну сторону от точки A или С в зависимости от того, лежат ли точки A1 на отрезке BC или точка C1 на отрезке AB и снова следует из равенства с необходимостью совпадения точек B1 и B1. Для рассмотрения общего случая снова проведем через вершину B прямую a параллельную прямой AC (справа на рисунке ). Треугольник AC1C подобен треугольнику BC1M.
Слайд 15Отсюда следует
из подобия треугольников AA1C и NA1B получаем
Наконец,
из гомотетичности относительно центра O треугольников ONM и OAC имеем
Слайд 16Перемножая соответственно левые и правые части равенств, получаем искомое равенство.
Доказательство достаточности аналогично случаю основной теоремы.
Приведем некоторые следствия из
теоремы Чевы. 
Слайд 18Следствие 14.2.
Биссектрисы треугольника пересекаются в одной точке.
Доказательство:
Действительно из свойства биссектрис
можно записать следующие равенства:
Слайд 19Следствие 14.3.
Прямые, соединяющие вершины треугольника с точками касания вписанного в
него треугольника, пересекаются в одной точке. Эта точка называется точкой
Жергона. Из свойства касательных, проведенных из одной точки к окружности имеем: AB1 = AC1; BA1 = BC1 и CA1 = CB1. Отсюда следует равенство из теоремы Чевы и доказательство следствия 14.3.
Слайд 20Следствие 14.4. Высоты треугольника пересекаются в одной точке.
Доказательство:
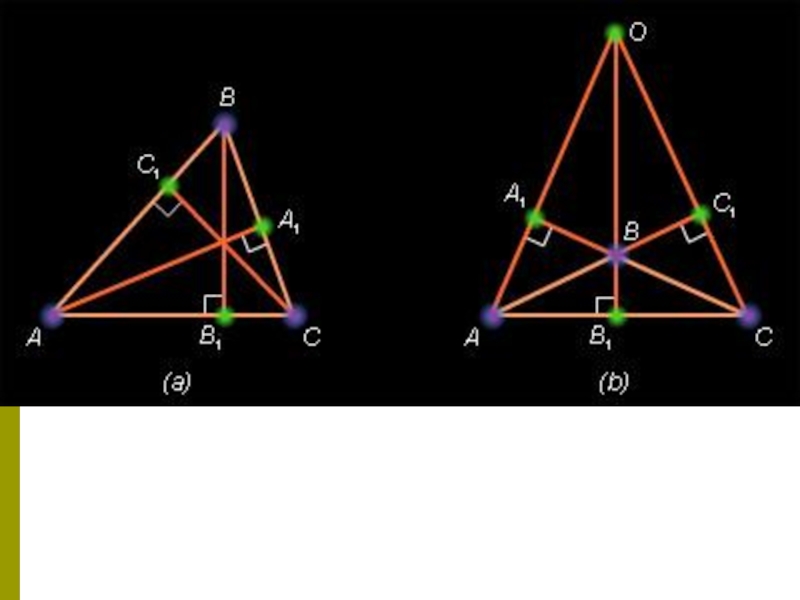
Рассмотрим 2 случая.
1. Пусть треугольник ABC остроугольный (рис. 14.1.3, a). Имеем
Отсюда
следует Следствие доказано.
Слайд 22Пусть треугольник ABC тупоугольный (см. рис. ). Применим в этом случае
обобщенную теорему Чевы. Тогда аналогично случаю 1 можно записать такие
же соотношения с учетом знака. Имеем
Отсюда следует доказательство.
