с развитием механики в математику проникают идеи изменения и
движения. В это время начинает складываться представление о функции как о зависимости одной переменной величины от другой.Французский математик Рене Декард (именем
которого и названа декардова система координат)
представлял себе функцию как зависимость
ординаты точки кривой от её абсциссы.
Термин «функция» (от латинского functio – исполнение, совершение) впервые ввёл немецкий математик Готфрид Лейбниц.









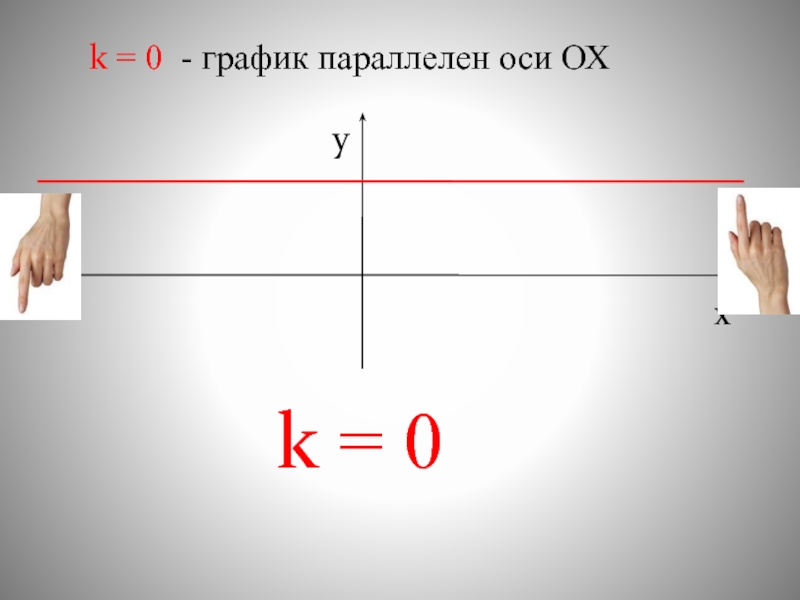
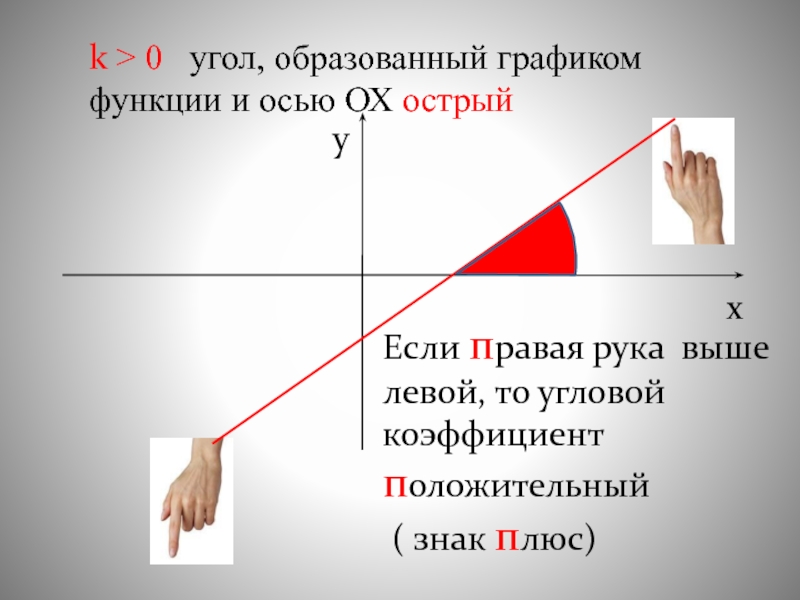 0 угол, образованный графиком функции и осью ОХ острыйхyЕсли" alt="k > 0 угол, образованный графиком функции и осью ОХ острыйхyЕсли правая рука выше левой, то">
0 угол, образованный графиком функции и осью ОХ острыйхyЕсли" alt="k > 0 угол, образованный графиком функции и осью ОХ острыйхyЕсли правая рука выше левой, то">