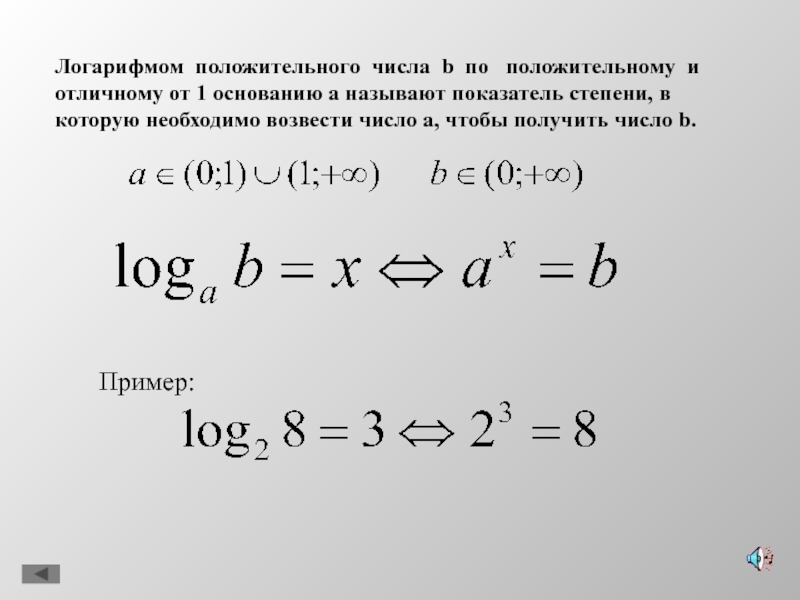Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Логарифмическая функция
Содержание
- 1. Логарифмическая функция
- 2. Содержание1. Понятие логарифма.2. Графики логарифмических функций.3. Свойства логарифмов.4. Решение логарифмических уравнений.5. Решение логарифмический неравенств.завершить
- 3. Логарифмом положительного числа b по положительному
- 4. В зависимости от значения основания приняты два
- 5. Можно выделить три формулыИз определения логарифма следует следующее тождество:Примеры:
- 6. Графики логарифмических функции1. y = lg x2.
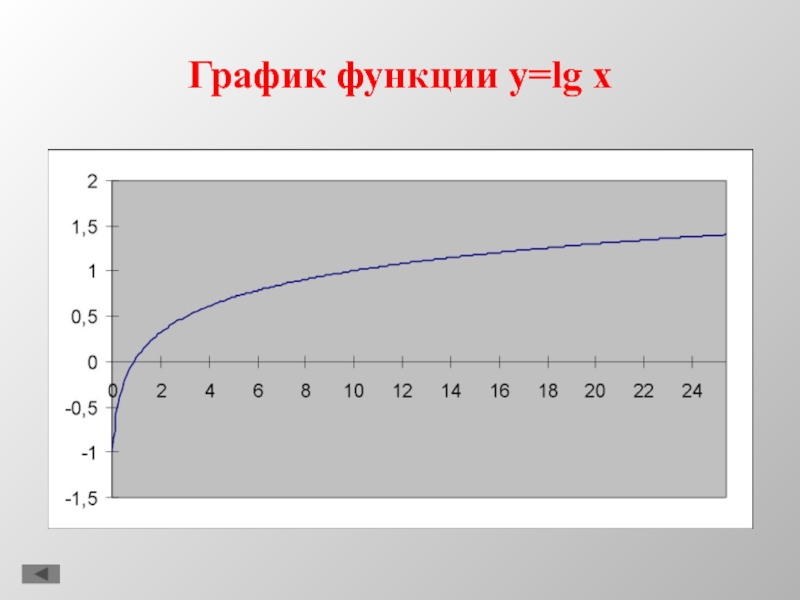
- 7. График функции y=lg x
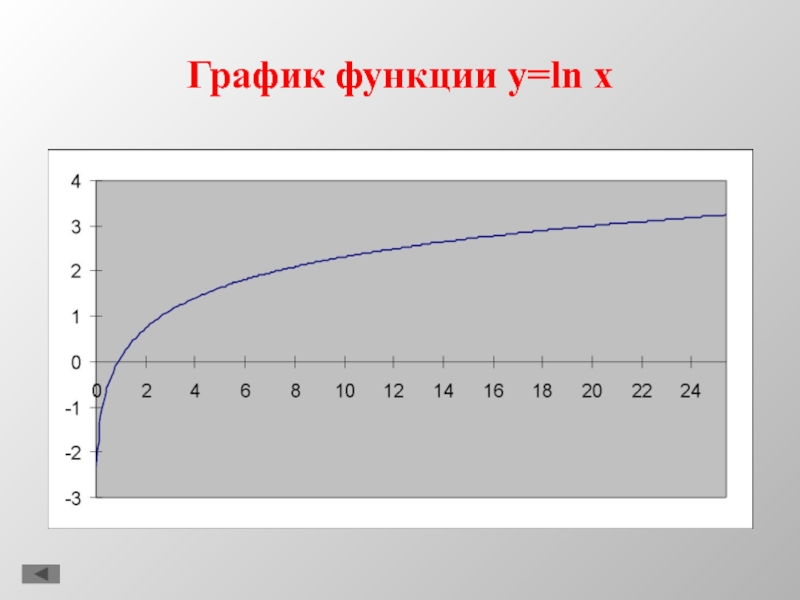
- 8. График функции y=ln x
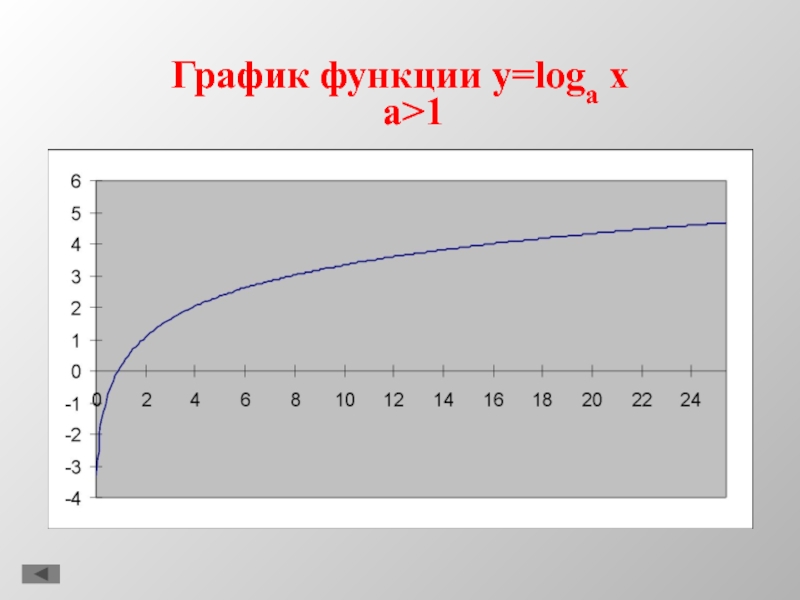
- 9. График функции y=loga xa>1
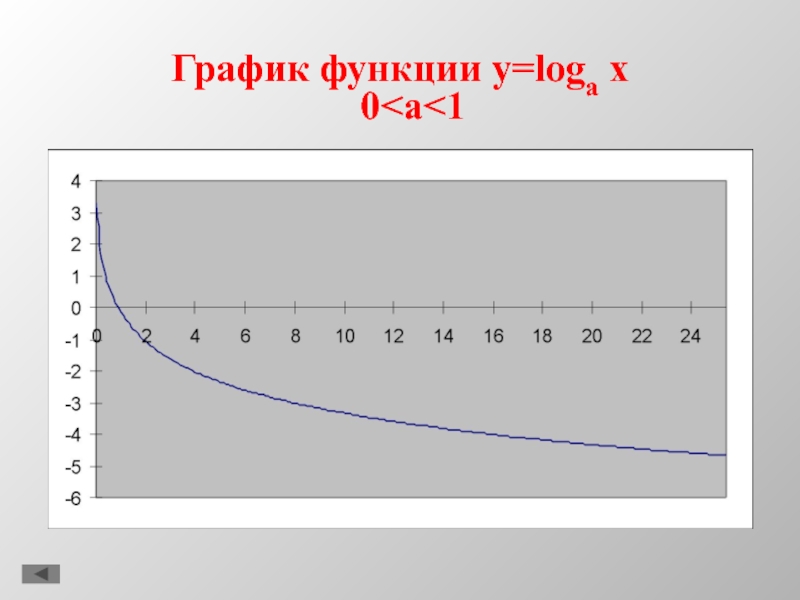
- 10. График функции y=loga x0
- 11. Свойства f(x)=loga xD(f)=(0;+∞);Не является ни четной, ни нечетной;При a>1 функция возрастающая, при 0
- 12. Свойства логарифмов1. Логарифм произведения.2. Логарифм частного.3. Логарифм
- 13. 1. Логарифм произведения равен сумме логарифмов множителей:2. Логарифм частного равен логарифмов делимого без логарифма делителя:
- 14. 3. Логарифм степени равен произведению показателя степени
- 15. 5. Переход от одного основания к другому
- 16. Свойства натуральных логарифмовЧтобы по известному десятичному логарифму
- 17. Решения логарифмических уравнений
- 18. Решить уравнение:Значит,
- 19. Решение логарифмических неравенств
- 20. Решите неравенство:
- 21. Над презентацией работали:Киселев МихаилТаячков МаксимКирилов ДмитрийСпасибо за внимание
- 22. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Содержание
1. Понятие логарифма.
2. Графики логарифмических функций.
3. Свойства логарифмов.
4. Решение логарифмических
уравнений.
Слайд 3Логарифмом положительного числа b по положительному и отличному от
1 основанию а называют показатель степени, в которую необходимо возвести
число а, чтобы получить число b.Пример:
Слайд 4В зависимости от значения основания приняты два обозначения
Если основанием является
10, то вместо log10 x пишут lg x.
Для введения
следующего определения стоит понимать что за число e.
Число е есть предел, к которому стремится при неограниченном возрастании n. Т.е
Вместо loge x принято писать ln x.Слайд 6Графики логарифмических функции
1. y = lg x
2. y = ln
x
3. y = loga x, a>1
4. y = loga x,
0содержание
Слайд 11Свойства f(x)=loga x
D(f)=(0;+∞);
Не является ни четной, ни нечетной;
При a>1 функция
возрастающая, при 0
минимального значения;Непрерывна;
E(f)=(- ∞;+ ∞);
Асимптота х=0;
Выпукла вверх при a>1, выпукла вниз при 0
Слайд 12Свойства логарифмов
1. Логарифм произведения.
2. Логарифм частного.
3. Логарифм степени.
4. Логарифм корня.
5.
Переход от одного показателя к другому.
6. Свойства натуральных логарифмов.
содержание
Слайд 131. Логарифм произведения равен сумме логарифмов множителей:
2. Логарифм частного равен
логарифмов делимого без логарифма делителя:
Слайд 143. Логарифм степени равен произведению показателя степени на логарифм ее
основания:
4. Логарифм корня равен отношению логарифма подкоренного выражения и показателя
корня:Слайд 16Свойства натуральных логарифмов
Чтобы по известному десятичному логарифму числа х найти
его натуральный логарифм, нужно разделить десятичный логарифм числа х на
десятичный логарифм числа е:Чтобы по известному натуральному логарифму числа х найти его десятичный логарифм, нужно умножить натуральный логарифм числа х на десятичный логарифм числа е:
Число lg e=0.43429 называется модулем десятичных логарифмов и обозначается через М.