Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
М А Т Е М А Т И Ч Е С К И Е И Г Р Ы
Содержание
- 1. М А Т Е М А Т И Ч Е С К И Е И Г Р Ы
- 2. М А Т Е М А Т
- 3. Если исходное число камней делится на 3,
- 4. Задача 2. Двое играют, поочередно выставляя крестики
- 5. ХОХОХООООООООООХХХХХХХХХХООООООООООХХХХХХХХХХООООООООООХХХХХХХХХХХХХХХХХХООООООООРЕШЕНИЕ:
- 6. Задача 3. Двое играющих по очереди красят
- 7. Решение:Первый. В какой-то момент (можно на первом
- 8. Ч И С Л О В Ы
- 9. №1 Животноводческий ребус.Б + Б Е Е
- 10. №2 Нитки и ткань. НИТКА + НИТКА ТКАНЬОтвет: 15306 + 15306 = 30612.
- 11. №3 Вагоны.ВАГОН + ВАГОН = СОСТАВ Ответ: 85679 + 85679 = 171358.
- 12. №4 Собака и кошки.КОШКА + КОШКА +
- 13. №5. Ищем зеркальную пару чисел.Два числа называются
- 14. Решение:Ясно, что числа зеркальной пары будут трехзначными:
- 15. Принцип ДирихлеЗапишем принцип Дирихле: если по N
- 16. 1тип задач «Сколько нужно взять?..»1. В мешке
- 17. 2. В коробке лежат карандаши: 7 красных
- 18. 2 тип задач «Докажите, что найдутся двое...»1.
- 19. 2 тип задач «Докажите, что найдутся двое...»2.
- 20. 3 тип задач. Обобщенный принцип Дирихле: 1.
- 21. 3 тип задач. Обобщенный принцип Дирихле: 2.
- 22. Принцип Дирихлевывод:Таким образом, применяя данный метод, необходимо:1)Определить,
- 23. Задача 1. Три клоуна Бим, Бам и Бом
- 24. Ответ: Бим одет в красную рубашку и
- 25. Задача 2. Три курицы снесли за три
- 26. Три курицы снесли за 3 дня 3
- 27. Задача 3. Когда отцу было 27 лет,
- 28. З А Д А Ч И
- 29. Задача 2. Возраст брата составляет 40% от
- 30. Задача 3. В начале года число мужчин,
- 31. Решение:Число мужчин, работавших на заводе в начале
- 32. З А Д А Ч И
- 33. Задача 2. На каждой кочке в маленьком
- 34. Задача 3. У двузначного числа "n" цифра
- 35. З А Д А Ч И
- 36. Задача 2. Разделите прямоугольник на 4 равные
- 37. Задача 3. Преуспевающий торговецнедвижимостью купил 16 акровземли.
- 38. Задача 4. Расположите на 16 клетках 4
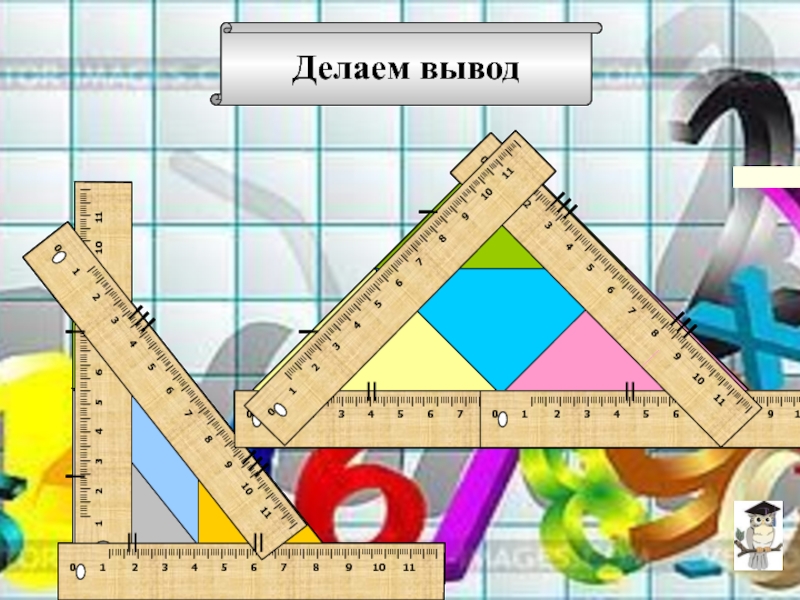
- 39. Задача 5. Разделите прямоугольный треугольникна четыре равных треугольника.Ответ
- 40. Делаем вывод
- 41. Задача 6. Разделите произвольный треугольникна девять равных треугольника.Ответ
- 42. Задача 7. Не отрывая карандаша от бумаги
- 43. Слайд 43
- 44. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Презентацию подготовила учитель математики МБОУ «Федоровская СОШ №2 с углублённым
изучением отдельных предметов»
Слайд 2М А Т Е М А Т И Ч Е
С К И Е И Г Р Ы
Задача
1. Двое по очереди берут из кучи камни. Разрешается брать любую степень двойки (1, 2, 4...). Взявший последний камень выигрывает. Кто победит в этой игре?Слайд 3Если исходное число камней делится на 3, то выигрывает второй,
беря каждый раз по 1 или 2 камня и оставляя
число камней, которое делится на 3Решение:
20
22
21
23
Слайд 4Задача 2. Двое играют, поочередно выставляя крестики и нолики на
квадратном поле 9х9. В конце каждый получает очко за каждую
строку и столбец, в которых его знаков больше. Сможет ли первый игрок выиграть?Слайд 6Задача 3. Двое играющих по очереди красят полоску из 150
клеток: первый всегда красит две клетки подряд, а второй -
три. Проигрывает тот, кто не может сделать ход. Кто должен выиграть при правильной игре?Слайд 7Решение:
Первый. В какой-то момент (можно на первом ходу) он оставляет
незакрашенный просвет в две клетки и не трогает его, пока
есть не менее трёх незакрашенных клеток подряд.Слайд 8Ч И С Л О В Ы Е З
А Д А Ч И
Требуется расшифровать запись арифметического равенства, в
котором цифры заменены буквами, причем разные цифры заменены разными буквами, одинаковые - одинаковыми. Предполагается, что исходное равенство верно и записано по обычным правилам арифметики. В частности, в записи числа первая слева цифра не является цифрой 0; используется десятичная система счисления.Слайд 9№1 Животноводческий ребус.
Б + Б Е Е Е = М
У У У
Так как при сложении данных чисел цифра
Е в разряде десятков поменялась на цифру У, то суммой однозначных чисел Б и Е является двузначное число, начинающееся с единицы. Так как помимо увеличения на единицу цифры в разряде десятков также изменилась и цифра в разряде сотен, то Е = 9, Б = 1, У = 0. Ответ.1 + 1999 = 2000.
Слайд 12№4 Собака и кошки.
КОШКА + КОШКА + КОШКА = СОБАКА
Ответ:
Первый вариант: 56350 +56350 + 56350 = 169050
Второй: 57350 + 57350 + 57350 = 172050Слайд 13№5. Ищем зеркальную пару чисел.
Два числа называются зеркальной парой
чисел,
если порядок цифр в одном из них
слева направо такой
же самый, как порядок цифр другого числа
справа налево.
Произведение какой зеркальной
пары чисел равно 92565?
Ответ: 165 и 561
Слайд 14Решение:
Ясно, что числа зеркальной пары будут трехзначными:
abc · cba=92565
Первый вывод: a=5 (последняя цифра произведения =5),
с-должно быть нечетное
и меньше 3, иначе 5b3 · b5 > 92565 следовательно с=1.
Получим: 1b5
5b1
1b5
??b*5
?b* 55
9 2 5 6 5
Из суммы второго столбца b+(b*5)=?6 или 6*b=?6,
следовательно b=1 или 6.
Получим либо 115 и 511, либо 165 и 561, перемножив находим , что подходит 165 и 561.
Слайд 15Принцип Дирихле
Запишем принцип Дирихле: если по N разложить предметы, число
которых M больше N, то найдется ящик, в котором будет
находится больше одного предмета.На первый взгляд непонятно, почему это совершенно очевидное предложение, тем не менее, является мощным математическим методом решения задач, причем, самых разнообразных. Дело в том, что в каждой конкретной задаче нелегко понять, что же здесь выступает в роли «предметов», а что – в роли «ящиков».
П Р И Н Ц И П Д Е Р И Х Л Е
Слайд 161тип задач «Сколько нужно взять?..»
1. В мешке лежат шарики двух
разных цветов. Какое наименьшее число шариков нужно вынуть из мешка,
чтобы среди ни обязательно оказались два шарика одного цвета?Решение:
Здесь роль предметов играют шарики (М=?), роль ящиков - цвета (N=2).Чтобы M>N, т.е. в одном ящике оказалось два предмета, их должно быть больше двух, т.е. М=3
1тип задач «Сколько нужно взять?..»
Слайд 172. В коробке лежат карандаши: 7 красных и 5 синих.
В темноте берут карандаши. Сколько карандашей надо взять, чтобы среди
них было не менее 2 красных и не менее 3 синих?Решение: Если предположить, что сначала будут попадаться только красные карандаши, то для того, чтобы было 3 синих, нужно взять 7(красные)+3(N)=10. Это «худший» вариант развития событий, т.к. красных карандашей больше.
Слайд 182 тип задач «Докажите, что найдутся двое...»
1. При каком наименьшем
количестве учеников школы среди них обязательно найдутся двое, у которых
день и месяц рождения совпадают?Решение: Дней в году N=365 или 366,то принципу Дирихле М= 366 или 367.
2 тип задач «Докажите, что найдутся двое...»
Слайд 192 тип задач «Докажите, что найдутся двое...»
2. В лесу растет
миллион елок. Известно, что на каждой из них не более
600 000 иголок. Докажите, что в лесу найдутся хотя бы две елки с одинаковым числом иголок.Решение: Если предположить, что у всех елок разное количество иголок, то таких елок 600 000 (это ящики, N= 600 000), а по условию елок 1000 000=М, то М>N,по принципу Дирихле найдутся хотя бы две елки «в одном ящике», т.е. с одинаковым количеством иголок.
Слайд 203 тип задач. Обобщенный принцип Дирихле:
1. В магазин привезли
25 ящиков с яблоками трех сортов, причем в каждом ящике
лежали яблоки какого-то одного сорта. Можно ли найти 9 ящиков с яблоками одного сорта?Решение. 25:3=8 (ост.1). 25=8*3+1. к=3, N=8, M>N, то принципу Дирихле найдутся хотя бы один ящик, в котором находятся более, чем к=3 предметов, т.е. 4 предмета.
3 тип задач. Обобщенный принцип Дирихле:
Слайд 213 тип задач. Обобщенный принцип Дирихле:
2. На площадке 20
собак восьми разных пород. Докажите, что среди них есть не
менее трех собак одной породы.Решение: 20:8=2(ост. 4), 20=8*2+4. к=2,N=8, М>N, то по принципу Дирихле найдутся хотя бы три собаки одной породы.
Слайд 22Принцип Дирихле
вывод:
Таким образом, применяя данный метод, необходимо:
1)Определить, что удобно в
задаче принять за «предметы», а что за «ящики».
2)Получить «ящики».Чаще всего,
их должно быть больше, чем предметов.3)Выбрать для решения требуемую формулировку принципа Дирихле.
Слайд 23Задача 1. Три клоуна Бим, Бам и Бом вышли на арену
в красной, зеленой и синей рубашках. Их туфли были тех
же цветов. У Бима цвета рубашки и туфельсовпадали. У Бома ни туфли,
ни рубашка не были
красными. Бам был в
зеленых туфлях, а
в рубашке другого цвета.
Как были одеты клоуны?
Л О Г И Ч Е С К И Е З А Д А Ч И
Слайд 24Ответ: Бим одет в красную рубашку и красные туфли, Бам
в синей рубашке и зеленых туфлях, Бом в зеленой рубашке
и туфлях синего цвета.Решение:
Слайд 25Задача 2. Три курицы снесли за три дня три яйца.
Сколько яиц снесут двенадцать кур за двенадцать кур за двенадцать
дней?Слайд 26Три курицы снесли за 3 дня 3 яйца, следовательно,
3 крицы снесут за 12 дней в 4 раза больше
яиц,а 12 кур за 12 дней еще в 4 раза больше, т.е. 48 яиц.
Решение задачи удобно записать в виде таблицы:
Количество кур Количество дней Количество яиц
3 3 3
3 12 3х4=12
12 12 12х4=48
Решение:
Слайд 27Задача 3. Когда отцу было 27 лет, сыну было 3
года. Сейчас сыну в три раза меньше лет, чем отцу.
Сколько лет каждому из них?Решение:
Разница в возрасте между отцом и сыном неизменна и равна 24 годам. Сыну в три раза меньше лет, чем отцу, поэтому 24 года - это удвоенный возраст сына. Следовательно, сыну сейчас 12 лет, а отцу 36 лет.
Слайд 28З А Д А Ч И Н А
П Р О Ц Е Н Т Ы
Задача 1. Собрали
100 кг грибов. Оказалось, что их влажность 99%. Когда грибы подсушили, влажность снизилась до 98%. Какой стала масса этих грибов после подсушивания?Решение:
В 100 кг грибов содержится, по условию, 99 кг воды и 1 кг сухого вещества. После подсушивания сухое вещество стало составлять 2% .Но если 2% составляют 1 кг, то вся масса грибов равна 50 кг.
Слайд 29Задача 2. Возраст брата составляет 40% от возраста сестры. Сколько процентов
составляет возраст сестры от возраста брата?
Решение:
Примем возраст сестры за 100%.Возраст
брата составит 40%.Процентное отношение возраста сестры к возрасту брата равно: (100/40) · 100% = 250%.
Слайд 30Задача 3. В начале года число мужчин, работавших на заводе,
составляло 40% от общей численности работников завода. После того, как
были приняты на работу еще 6 мужчин, а 5 женщин уволилось, число мужчин и женщин на заводе сравнялось. Сколько человек работало на заводе в начале года?Слайд 31Решение:
Число мужчин, работавших на заводе в начале года, было на
11 меньше числа работавших там женщин. Процентная разность между числом
женщин и числом мужчин составляла в начале года 20%.Общая численность работавших на заводе в это время - 11:0,2 = 55 человек.
Слайд 32З А Д А Ч И Н А
Д Е Л И М О С Т Ь
Задача 1.
Остаток от деления 100 на некоторое число равен 4. При делении 90 на это же число в остатке получается 18. На какое число делили? Решение:
Из условия следует, что 100-4=96 делится на искомое число. Также 90-18=72 делится на искомое число.
Их разность также делится на искомое число:
96-72=24. Следовательно, искомое число - 24, так как на него делится и 96, и 72.
Слайд 33Задача 2. На каждой кочке в маленьком болотце сидят не
меньше , чем по 3 лягушки, а всего лягушек -
145 .Тогда число кочек в этом болотце не может равняться:( A )1; (B) 23; (C) 31; ( D ) 44; ( E ) 55;
Решение:
Разделим 145 на 3 и узнаем максимальное количество кочек в болотце, когда на каждой из них разместится не меньше 3 лягушек и получим 48.
Перебирая ответы , остановимся на ответе (Е), как на единственном (55 больше 48).
Ответ: 55.
Слайд 34Задача 3. У двузначного числа "n" цифра десятков в два
раза больше, чем цифра единиц. Тогда число "n" обязательно:
( A
) четное; (B) нечетное(C) меньше 20; ( D ) делится на 3; ( E ) делится на 6.
Решение:
Ищем число "n" среди ряда чисел: 10 - 99.
По условию, у всех подозреваемых чисел - десятки четны (2,4,6,8), а единицы - в два раза меньше (1,2,3,4,).
Перечислим все эти числа: 21, 42, 63, 84.
Все они делятся на 3.
Следовательно верен ответ (D).
Слайд 35З А Д А Ч И С Г
Е О М Е Т Р И Ч Е С
К И МС О Д Е Р Ж А Н И Е М
Задача 1. Сколько углов образуют 5 различных лучей, направленных из одной точки?
Решение:
Принцип решения следующий:
n – количество лучей, но каждый последующий луч образует еще один угол, следовательно искомое количество углов ищем по формуле
Ответ: 20 углов
Слайд 36Задача 2.
Разделите прямоугольник на 4 равные части
по величине
и по форме так, чтобы в каждой
из них находился один
кружочек.Ответ (4)
Слайд 37Задача 3.
Преуспевающий торговец
недвижимостью купил 16 акров
земли. Он решил разбить
площадь
на 16 одноакровых участков под жилые
дома так, чтобы все участки
были одногоразмера и той же формы, что и основной
участок. Как это сделать?
Ответ
Слайд 38Задача 4.
Расположите на 16 клетках 4 монеты одного
достоинства и
4 монеты другого так, чтобы
ни в одном ряду – горизонтальном,
вертикальномили диагональном – не встречалось по 2 одинаковые монеты.
Ответ (4)