Слайд 2Тема урока: «Логарифмические неравенства»
В современной школе основной формой
обучения математике ,главным связующем звеном в интеграции различных организационных форм
обучения по-прежнему остается урок. В процессе обучения математический материал осознается и усваивается преимущественно в процессе решения задач, потому на уроках математики теория не изучается в отрыве от практики. Для того чтобы успешно решать логарифмические уравнения и неравенства , на которые в учебном плане отведено всего 4 часа, необходимо уверенное владение формулами для логарифмов и свойствами логарифмической функции. Тема « Логарифми-ческие неравенства» в учебном плане следует за темой: «Логарифмические уравнения».
Ситуация несколько осложняется по сравнению с решением логарифмических уравнений, так как здесь приходится решать систему неравенств, состоящую из решения самого логарифмического неравенства и области определения функции.
Слайд 3“Изобретение логарифмов, сократив работу астронома, продлило ему жизнь»
Цели урока:
Образовательные:
1.Ознакомить и закрепить основные методы решения логарифмических неравенств, повторение понятия
логарифма, повторение основных свойств логарифмов, предупредить появления типичных ошибок.
2.Предоставить каждому обучающему возможность проверить свои знания и повысить их уровень.
3.Активизировать работу класса через разные формы работы.
развивающие:
1. Продолжить формирование ЗУН
2. Развивать навыки самостоятельной работы и самоконтроля.
3. Развивать логическое мышление, умение говорить и слушать.
воспитательные:
1.Воспитывать ответственное отношение к труду.
2.Воспитывать волю и настойчивость , для достижение конечных результатов.
3.Воспитывать аккуратность и последовательность выполнения действий.
Слайд 4Тема урока: « Логарифмические неравенства»
Тип урока: Урок ознакомления с новым
материалом
Оборудование : Мультимедиа.
1Организационный момент:
2.Актуализация опорных знаний;
Вычислить:
1. Индивидуальные работы по карточкам-заданиям
Карточка №1
Log64+log69
Log1/336-log1/312
Карточка №2
Log36+log33/2
Log1/264-log1/28
Карточка №3
Log36+log31/2
Log1/354-log1/32
Слайд 5Самостоятельное решение учащихся у доски:
1 ученик
Log3x=2log38-1/2log316
2
ученик
Log5x=4log53-1/3log527
Задать вопрос: Обязательно в конце при
решении логарифмических уравнений, что необходимо делать?
А почему необходимо делать проверку в конце?
Остальные работают с учителем, отвечая на его вопросы:
Что называют логарифмом числа?
Что такое десятичный логарифм?
Что такое натуральный логарифм?
Когда логарифмическая функция считается возрастающей, а когда убывающей?
Вычислите:
Log525; log71/49; log1/28; log41; lg10000; ln e
Log59 2log0,36 2+log45
5 0,3 4 log2log381
Найти ООФ y=log2(x+1); y=log3(1-x); y= log1/4(2x-3)
Подведение итогов по проверке знаний учащихся
Слайд 6Объяснение нового материала:
Решение логарифмических неравенств сводиться к решению системы неравенств,
содержащих ООФ и решение равносильного неравенства, полученного из логарифмического неравенства,
путем его преобразований по известным нам свойствам логарифмических функций.
Важным пунктом при решении логарифмического неравенства является так же монотонность функции:
1. Если Logax1
1 (т.е функция ↑)
x1
2. Если Logax1 x1>x2 (знак меняется на противоположный)
Слайд 7Решение логарифмических неравенств:
Решить:
1. Lg(x+1)≤2
ООФ x+1>0 → x>-1
Lg(x+1)≤lg102
Lg(x+1)≤lg100,
т.к ф-я ↑
x+1≤100
x≤100-1
x≤99
Находим общее между этим решением и ООФ
x
- 1 99
-1Ответ: - 1
Слайд 8Схема решения логарифмических неравенств
Найти ООФ
Решить логарифмическое неравенство, применяя :
- свойства логарифмов( сужать ООФ нельзя, т.е нельзя логарифмировать
);
- монотонность логарифмической функции( возрастание и убывания функции).
Выбрать общее решение
ООФ
решение неравенства
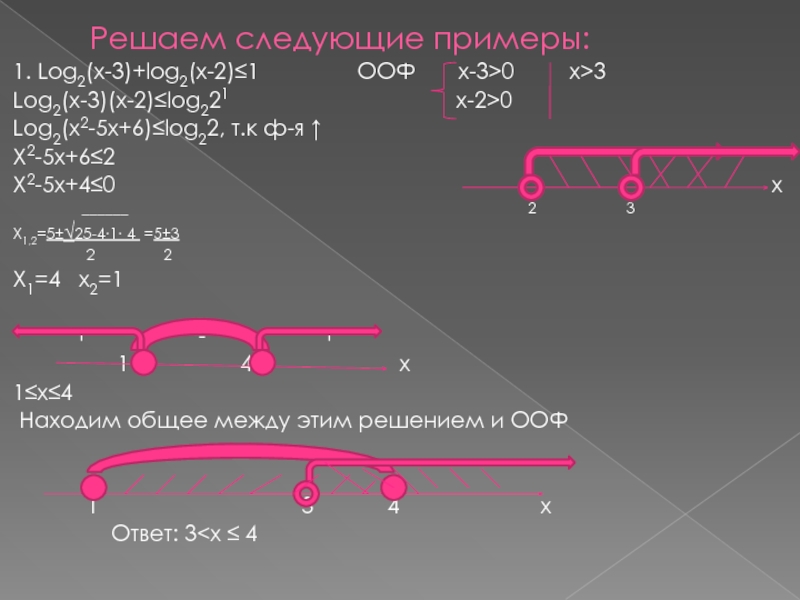
Слайд 9Решаем следующие примеры:
1. Log2(x-3)+log2(x-2)≤1
ООФ x-3>0
x>3
Log2(x-3)(x-2)≤log221 x-2>0
Log2(x2-5x+6)≤log22, т.к ф-я ↑
X2-5x+6≤2
X2-5x+4≤0 х
______ 2 3
X1,2=5±√25-4∙1∙ 4 =5±3
2 2
X1=4 x2=1
+ - +
1 4 x
1≤x≤4
Находим общее между этим решением и ООФ
1 3 4 x
Ответ: 3<х ≤ 4
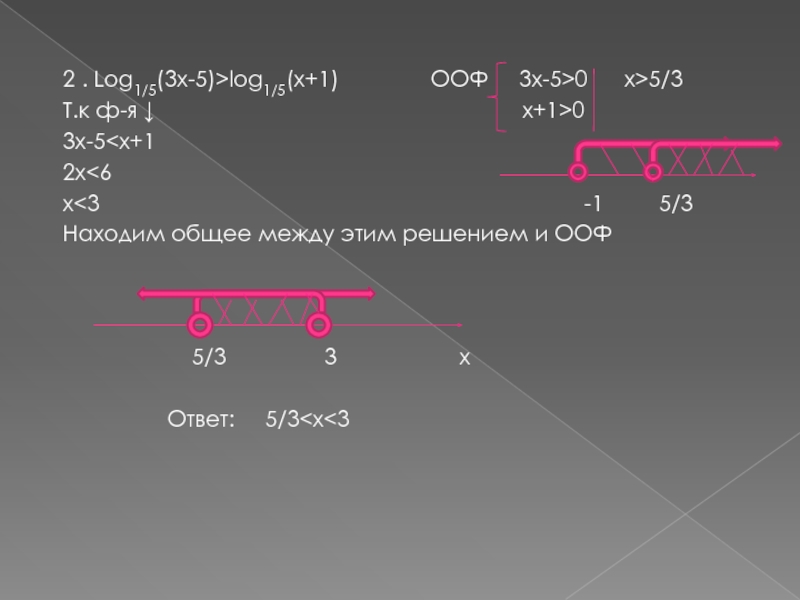
Слайд 102 . Log1/5(3x-5)>log1/5(x+1)
ООФ 3x-5>0 x>5/3
Т.к ф-я ↓
x+1>0
3x-52x<6
x<3 -1 5/3
Находим общее между этим решением и ООФ
5/3 3 x
Ответ: 5/3
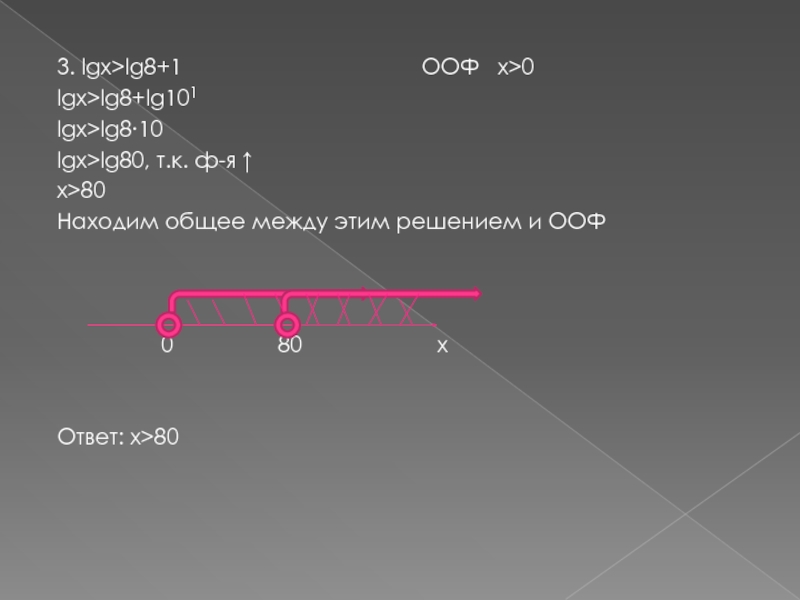
ООФ x>0
lgx>lg8+lg101
lgx>lg8∙10
lgx>lg80, т.к. ф-я ↑
x>80
Находим общее между этим решением и ООФ
0 80 x
Ответ: x>80
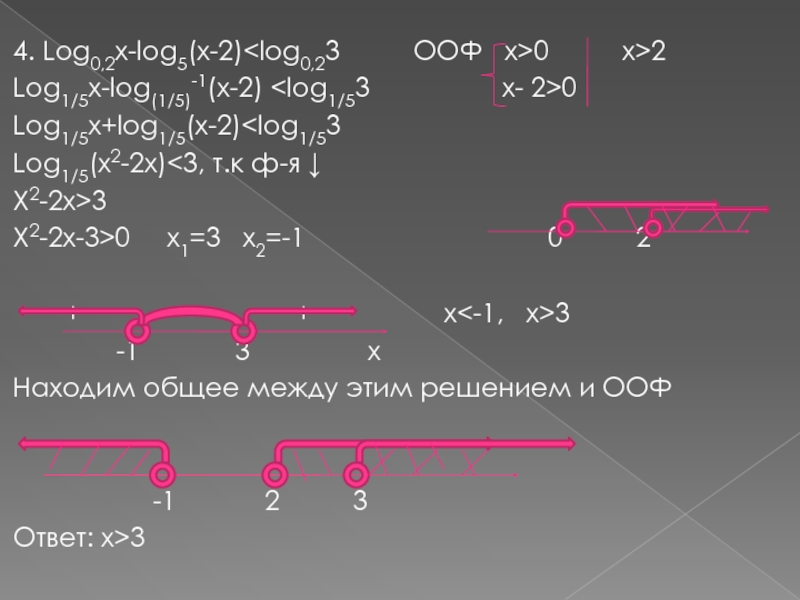
Слайд 124. Log0,2x-log5(x-2)0
x>2
Log1/5x-log(1/5)-1(x-2)
x- 2>0
Log1/5x+log1/5(x-2)Log1/5(x2-2x)<3, т.к ф-я ↓
X2-2x>3
X2-2x-3>0 x1=3 x2=-1 0 2
+ - + x<-1, x>3
-1 3 x
Находим общее между этим решением и ООФ
-1 2 3
Ответ: x>3
Слайд 13Закрепление пройденного материала
Самостоятельная работа
Слайд 14Домашнее задание
Решить:
Lg(x-1)2>lg(3x+1)
Lg(x+4)-lg(x-5)≤1
Lg2x+lg(3x+5)=2
Слайд 15Подведение итогов урока
Еще раз повторить схему решения логарифмических неравенств
Определить разницу
между решением логарифмических уравнений и логарифмических неравенств
Объявление оценок