Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация по геометрии в 11 классе: "Многогранники вокруг нас"
Содержание
- 1. Презентация по геометрии в 11 классе: "Многогранники вокруг нас"
- 2. «Правильных многогранников вызывающе мало, но этот весьма
- 3. Существует пять удивительно симметричных и красивых многогранниковСуществует
- 4. тетраэдр-огоньТетра́эдр (τετραεδρον — четырёхгранник) — простейший многогранник, гранями которого являются четыре треугольника.
- 5. Свойства правильного тетраэдра:Каждая его вершина является вершиной
- 6. куб-земля
- 7. Свойства куба:Четыре сечения куба являются правильными шестиугольниками —
- 8. октаэдр-воздух
- 9. икосаэдр-вода
- 10. додекаэдр-вселенная
- 11. Число вершин, рёбер и граней правильных многогранников связано друг с другом интересным соотношением.
- 12. Кроме правильных многогранников существуют полуправильные или не
- 13. Слайд 13
- 14. Один из величайших математиков мира, работы которого
- 15. Создания природы красивы и симметричны. В кристаллографии существует раздел, который называется «геометрическая кристаллография»
- 16. «Мой дом построен по законам самой строгой архитектуры. Сам Евклид мог бы поучиться, познавая мою геометрию»
- 17. Слайд 17
- 18. Математика владеет не только истиной, но и
- 19. Спасибо завнимание
- 20. Скачать презентанцию
«Правильных многогранников вызывающе мало, но этот весьма скромный по численности отряд сумел пробраться в самые глубины различных наук»
Слайды и текст этой презентации
Слайд 3Существует пять удивительно симметричных и красивых многогранниковСуществует пять удивительно симметричных
и красивых многогранников, у которых все грани одинаковы. Это: тетраэдр
(четырёхгранник)Существует пять удивительно симметричных и красивых многогранников, у которых все грани одинаковы. Это: тетраэдр (четырёхгранник), гексаэдр (шестигранник)Существует пять удивительно симметричных и красивых многогранников, у которых все грани одинаковы. Это: тетраэдр (четырёхгранник), гексаэдр (шестигранник), октаэдр (восьмигранник)Существует пять удивительно симметричных и красивых многогранников, у которых все грани одинаковы. Это: тетраэдр (четырёхгранник), гексаэдр (шестигранник), октаэдр (восьмигранник), додекаэдр (двенадцатигранник)Существует пять удивительно симметричных и красивых многогранников, у которых все грани одинаковы. Это: тетраэдр (четырёхгранник), гексаэдр (шестигранник), октаэдр (восьмигранник), додекаэдр (двенадцатигранник), икосаэдр (двадцатигранник)Существует пять удивительно симметричных и красивых многогранников, у которых все грани одинаковы. Это: тетраэдр (четырёхгранник), гексаэдр (шестигранник), октаэдр (восьмигранник), додекаэдр (двенадцатигранник), икосаэдр (двадцатигранник). У тетраэдраСуществует пять удивительно симметричных и красивых многогранников, у которых все грани одинаковы. Это: тетраэдр (четырёхгранник), гексаэдр (шестигранник), октаэдр (восьмигранник), додекаэдр (двенадцатигранник), икосаэдр (двадцатигранник). У тетраэдра, октаэдраСуществует пять удивительно симметричных и красивых многогранников, у которых все грани одинаковы. Это: тетраэдр (четырёхгранник), гексаэдр (шестигранник), октаэдр (восьмигранник), додекаэдр (двенадцатигранник), икосаэдр (двадцатигранник). У тетраэдра, октаэдра и икосаэдра Существует пять удивительно симметричных и красивых многогранников, у которых все грани одинаковы. Это: тетраэдр (четырёхгранник), гексаэдр (шестигранник), октаэдр (восьмигранник), додекаэдр (двенадцатигранник), икосаэдр (двадцатигранник). У тетраэдра, октаэдра и икосаэдра поверхности состоят из равносторонних треугольников. Куб или гексаэдр (шестигранник)Существует пять удивительно симметричных и красивых многогранников, у которых все грани одинаковы. Это: тетраэдр (четырёхгранник), гексаэдр (шестигранник), октаэдр (восьмигранник), додекаэдр (двенадцатигранник), икосаэдр (двадцатигранник). У тетраэдра, октаэдра и икосаэдра поверхности состоят из равносторонних треугольников. Куб или гексаэдр (шестигранник) имеет поверхность состоящую из шести квадратов. Поверхность додекаэдра состоит из двенадцати правильных пятиугольников. Эти многогранники называются правильными многогранникамиЭти многогранники называются правильными многогранниками или платоновыми телами в честь древнегреческого философа Платона, в философии которого они играли очень важную роль. ТетраэдрЭти многогранники называются правильными многогранниками или платоновыми телами в честь древнегреческого философа Платона, в философии которого они играли очень важную роль. Тетраэдр, кубЭти многогранники называются правильными многогранниками или платоновыми телами в честь древнегреческого философа Платона, в философии которого они играли очень важную роль. Тетраэдр, куб и октаэдрЭти многогранники называются правильными многогранниками или платоновыми телами в честь древнегреческого философа Платона, в философии которого они играли очень важную роль. Тетраэдр, куб и октаэдр были известны задолго Платона. А вот додекаэдрЭти многогранники называются правильными многогранниками или платоновыми телами в честь древнегреческого философа Платона, в философии которого они играли очень важную роль. Тетраэдр, куб и октаэдр были известны задолго Платона. А вот додекаэдр и икосаэдр Эти многогранники называются правильными многогранниками или платоновыми телами в честь древнегреческого философа Платона, в философии которого они играли очень важную роль. Тетраэдр, куб и октаэдр были известны задолго Платона. А вот додекаэдр и икосаэдр построил древнегреческий математик Теэтет - современник Платона. Четыре многогранника символизировали в учении Платона четыре стихии: тетраэдр Эти многогранники называются правильными многогранниками или платоновыми телами в честь древнегреческого философа Платона, в философии которого они играли очень важную роль. Тетраэдр, куб и октаэдр были известны задолго Платона. А вот додекаэдр и икосаэдр построил древнегреческий математик Теэтет - современник Платона. Четыре многогранника символизировали в учении Платона четыре стихии: тетраэдр - огонь, октаэдрЭти многогранники называются правильными многогранниками или платоновыми телами в честь древнегреческого философа Платона, в философии которого они играли очень важную роль. Тетраэдр, куб и октаэдр были известны задолго Платона. А вот додекаэдр и икосаэдр построил древнегреческий математик Теэтет - современник Платона. Четыре многогранника символизировали в учении Платона четыре стихии: тетраэдр - огонь, октаэдр - воздух, икосаэдрЭти многогранники называются правильными многогранниками или платоновыми телами в честь древнегреческого философа Платона, в философии которого они играли очень важную роль. Тетраэдр, куб и октаэдр были известны задолго Платона. А вот додекаэдр и икосаэдр построил древнегреческий математик Теэтет - современник Платона. Четыре многогранника символизировали в учении Платона четыре стихии: тетраэдр - огонь, октаэдр - воздух, икосаэдр - воду, куб Эти многогранники называются правильными многогранниками или платоновыми телами в честь древнегреческого философа Платона, в философии которого они играли очень важную роль. Тетраэдр, куб и октаэдр были известны задолго Платона. А вот додекаэдр и икосаэдр построил древнегреческий математик Теэтет - современник Платона. Четыре многогранника символизировали в учении Платона четыре стихии: тетраэдр - огонь, октаэдр - воздух, икосаэдр - воду, куб - землю. А додекаэдр выполнял как бы декоративную роль во вселенной в целом и символизировал гармонию мира. Согласно Платону, частицы огня, воздуха и воды имеют форму соответствующих многогранников и могут превращаться друг в друга, так как их грани подобны. Однако они не могут превращаться в частицы земли, квадратные грани которых не могут быть собраны из правильных треугольников. Позднее, другой греческий математик Евклид в своём знаменитом трактате "Начала" доказал, что нет других многогранников, кроме пяти платоновых тел, у которых грани были бы одинаковыми правильными многоугольниками. То есть нельзя построить или придумать тело, поверхность которого состоит из одинаковых правильных шестиугольников или семиугольников. Сам факт существования только пяти правильных многогранников удивителен, ведь на плоскости можно построить сколько угодно правильных многоугольников.Слайд 4тетраэдр-огонь
Тетра́эдр (τετραεδρον — четырёхгранник) — простейший многогранник, гранями которого являются
четыре треугольника.
Слайд 5Свойства правильного тетраэдра:
Каждая его вершина является вершиной трех треугольников. А
значит, сумма плоских углов при каждой вершине будет равна 180º.
В правильный тетраэдр можно вписать октаэдр, притом четыре (из восьми) грани октаэдра будут совмещены с четырьмя гранями тетраэдра, все шесть вершин октаэдра будут совмещены с центрами шести рёбер тетраэдра.
Правильный тетраэдр с ребром х состоит из одного вписанного октаэдра (в центре) с ребром х/2 и четырёх тетраэдров (по вершинам) с ребром х/2.
Правильный тетраэдр можно вписать в куб двумя способами, притом четыре вершины тетраэдра будут совмещены с четырьмя вершинами куба. Все шесть рёбер тетраэдра будут лежать на всех шести гранях куба и равны диагонали грани-квадрата.
Правильный тетраэдр можно вписать в икосаэдр, притом, четыре вершины тетраэдра будут совмещены с четырьмя вершинами икосаэдра.
Слайд 7Свойства куба:
Четыре сечения куба являются правильными шестиугольниками — эти сечения проходят
через центр куба перпендикулярно четырём его главным диагоналям.
В куб
можно вписать тетраэдр двумя способами. В обоих случаях четыре вершины тетраэдра будут совмещены с четырьмя вершинами куба и все шесть рёбер тетраэдра будут принадлежать граням куба. В первом случае все вершины тетраэдра принадлежат граням трехгранного угла, вершина которого совпадает с одной из вершин куба. Во втором случае попарно скрещивающиеся ребра тетраэдра принадлежат попарно противолежащим граням куба. Такой тетраэдр является правильным. В куб можно вписать октаэдр, притом все шесть вершин октаэдра будут совмещены с центрами шести граней куба.
Куб можно вписать в октаэдр, притом все восемь вершин куба будут расположены в центрах восьми граней октаэдра.
В куб можно вписать икосаэдр, при этом шесть взаимно параллельных рёбер икосаэдра будут расположены соответственно на шести гранях куба, остальные 24 ребра — внутри куба. Все двенадцать вершин икосаэдра будут лежать на шести гранях куба.
Диагональю куба называют отрезок, соединяющий две вершины, симметричные относительно центра куба. Диагональ куба находится по формуле , где d — диагональ, а — ребро куба.
Слайд 11Число вершин, рёбер и граней правильных многогранников связано друг с
другом интересным соотношением.
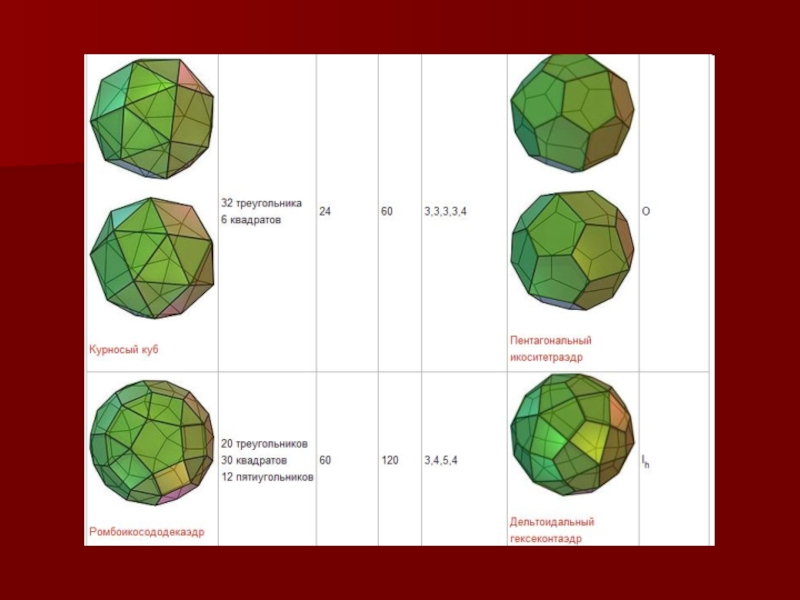
Слайд 12Кроме правильных многогранников существуют полуправильные или не совсем правильные многогранники.
Их впервые описал Архимед, в честь которого они названы архимедовыми
телами. Поверхность архимедовых тел состоит из правильных многоугольников разных типов. Например, треугольников и квадратов или квадратов и шестиугольников. Архимедовы тела состоят из граней разного типа. Если при соединении, грани какого либо типа пропускать, то получится открытый многогранник, просматриваемый не только снаружи, но и изнутри.Слайд 14Один из величайших математиков мира, работы которого оказали решающее влияние
на развитие многих современных разделов математики.
Л.Эйлер
(1707-1783)
Теорема Эйлера:
Число вершин -
число ребер + число граней =2Слайд 15Создания природы красивы и симметричны. В кристаллографии существует раздел, который
называется «геометрическая кристаллография»
Слайд 16«Мой дом построен по законам самой строгой архитектуры. Сам Евклид
мог бы поучиться, познавая мою геометрию»
Слайд 18Математика владеет не только истиной, но и высшей красотой -
красотой отточенной и строгой, возвышенно чистой и стремящейся к подлинному
совершенству, которое свойственно лишь величайшим образцам искусства.Бертран Рассел.