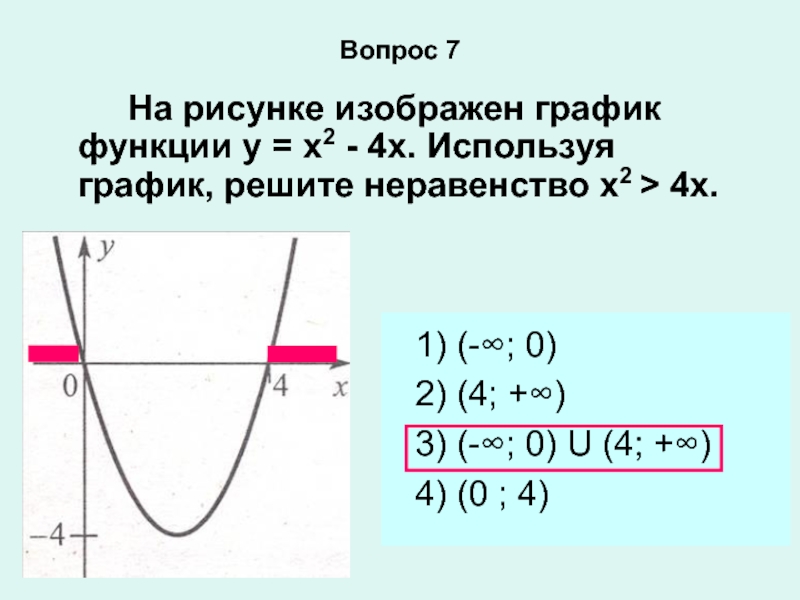
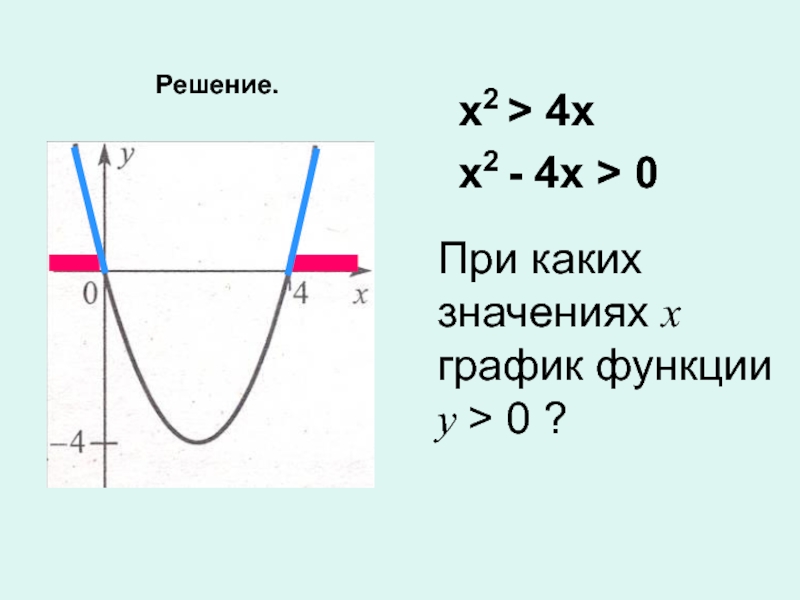
ли точка А (3;7) на графике функции
у = -х2 + 4х + 4?
Проходит ли прямая, заданная уравнением у = 5х + 2, через четвертую координатную четверть?
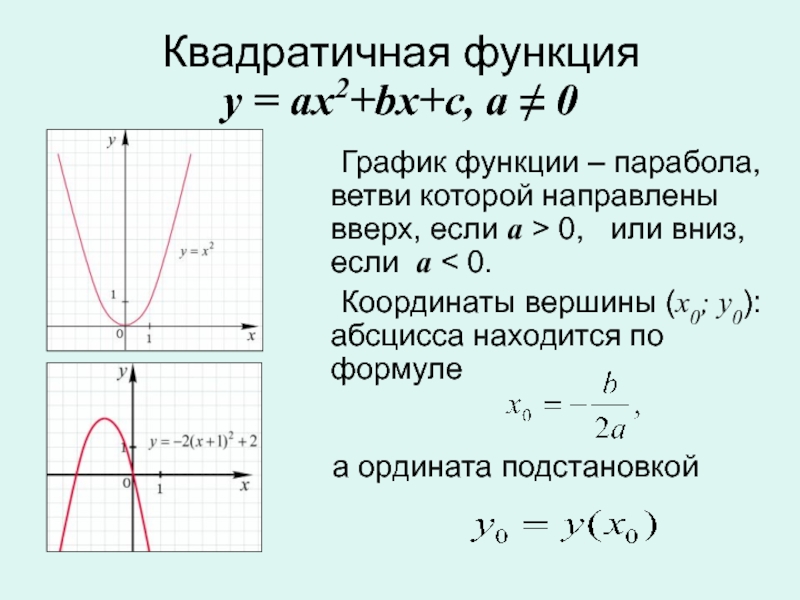
Найдите область значения функции у = (х -2)2 - 3.
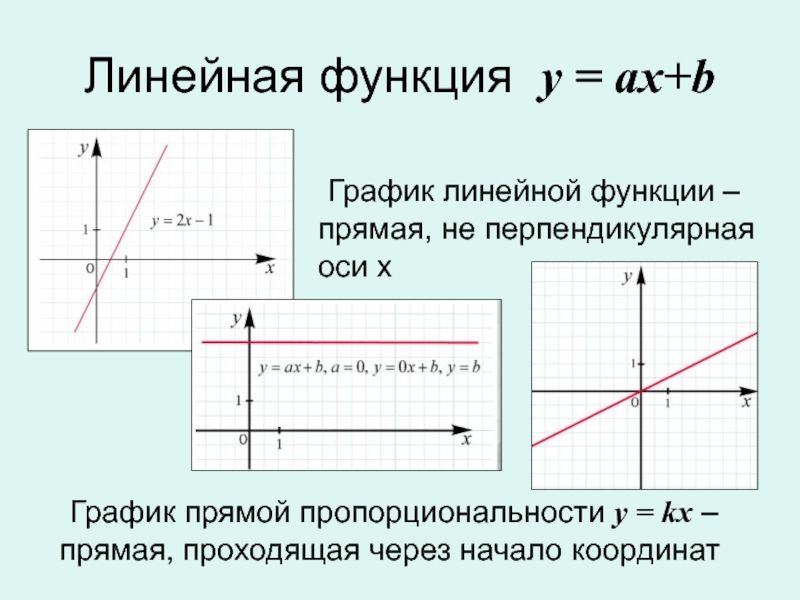
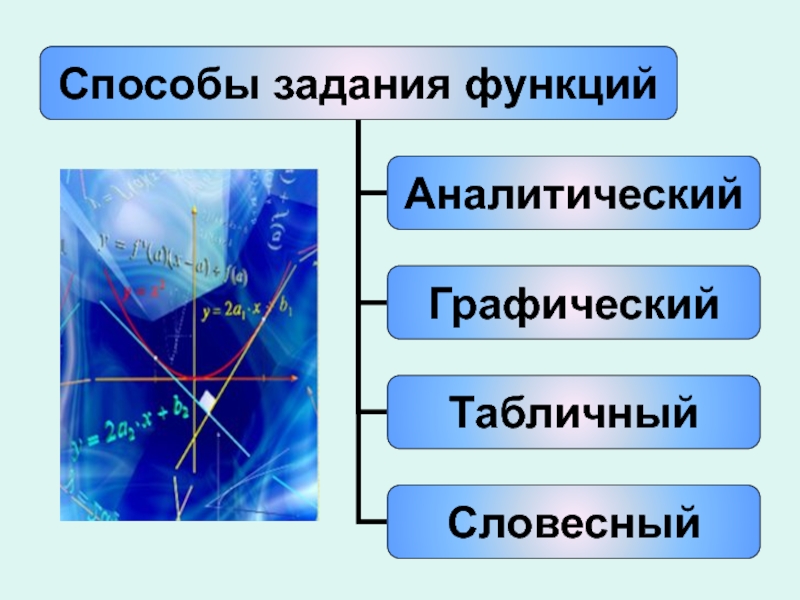
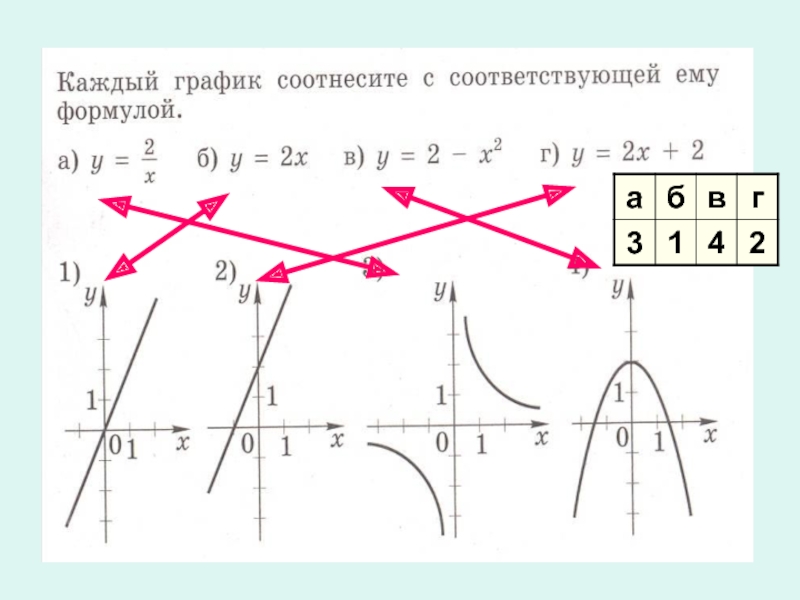
Функция задана уравнением у = 4х – 5. Какая линия служит графиком этой функции?
Найдите область определения функции
Лежит ли точка В ( 2;-5) на линии, заданной уравнением у = -х2+ 2х - 9?
Проходит ли прямая, заданная уравнением у = -3х – 5, через первую координатную четверть?
Найдите область значения функции у = - 2(х +1)2 + 3.
Функция задана уравнением у = (- 2/7) х +5. Какая линия служит графиком этой функции?
D (y): х > 6 или
D (y)= ( 6; + ∞ )
Да
Нет
Е(у): у ≥ -3 или
Е(у)= [-3; + ∞)
Прямая
Ответы
D (y): х ≤ 4 или
D (y)= (- ∞; 4]
Нет
Да
Е(у): у ≤ 3 или
Е(у)= ( - ∞; 3]
Прямая



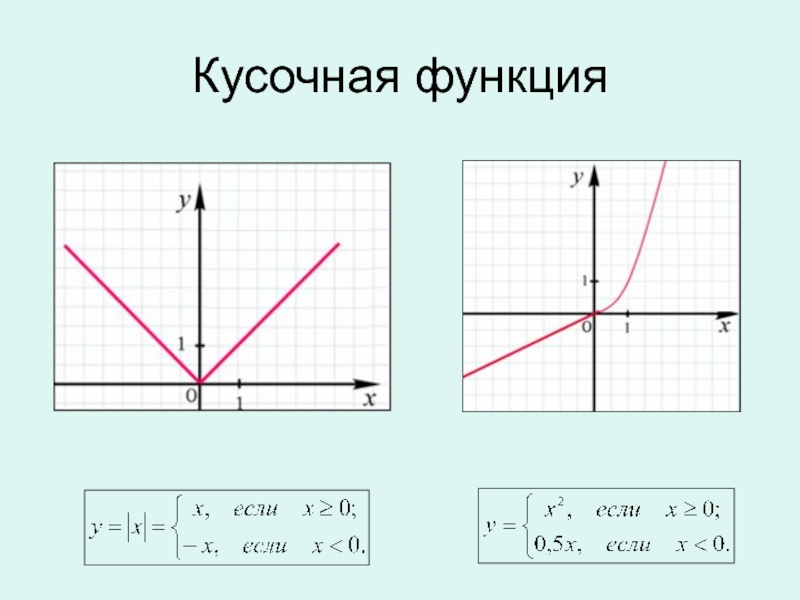

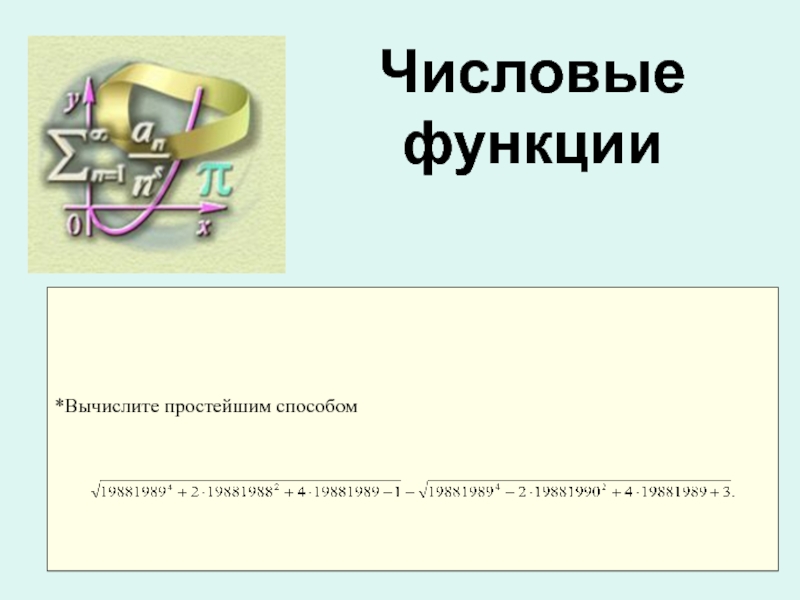
![Мастер-класс Изучение числовых функций, их свойств и графиков Функция целой части числа у = [x]D(у) = ( - ∞; + ∞) E (у) = Z Функция целой части числа у = [x]D(у) = ( - ∞; + ∞) E (у) = Z](/img/tmb/5/466228/6c80a3c3b79f9d7808707c151d0853f3-800x.jpg)











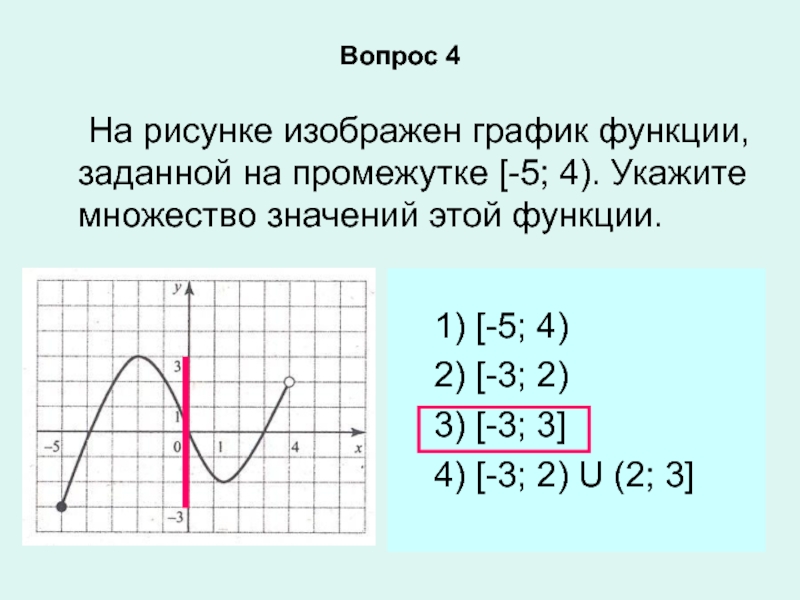
![Мастер-класс Изучение числовых функций, их свойств и графиков Вопрос 6На рисунке изображен график функции у = f(х), заданный на Вопрос 6На рисунке изображен график функции у = f(х), заданный на промежутке [ -1; 4,5]. Из приведенных](/img/thumbs/7007c90ec555dbd5d97059f9b48e3f88-800x.jpg)