Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математическая красота растений
Содержание
- 1. Математическая красота растений
- 2. ЧТО ТАКОЕ СИММЕТРИЯ? КАКИЕ ТОЧКИ НАЗЫВАЮТСЯ СИММЕТРИЧНЫМИ?Симметрия
- 3. СИММЕТРИЯ РАСТЕНИЙ!
- 4. ЦЕНТРАЛЬНАЯ СИММЕТРИЯ. Фигура называется симметричной относительно точки
- 5. ПРИМЕРЫ ЦЕНТРАЛЬНОЙ СИММЕТРИИ.Простейшими фигурами, обладающими центральной симметрией,
- 6. ЦЕНТРАЛЬНАЯ СИММЕТИРЯ В РАСТЕНИЯХЦентральную можно наблюдать на
- 7. ОСЕВАЯ (ЗЕРКАЛЬНАЯ) СИММЕТРИЯ.Фигура называется симметричной относительно прямой
- 8. ОСЕВАЯ СИММЕТРИЯ В РАСТЕНИЯХВ любом растении можно
- 9. ПОВОРОТНАЯ СИММЕТРИЯ.Предположим, что объект совмещается сам с
- 10. ПОВОРОТНАЯ СИММЕТРИЯ В РАСТЕНИЯХВеточка акации имеет зеркальную
- 11. ЧИСЛА ФИБОНАЧЧИ И РАСТЕНИЯ
- 12. ЗОЛОТОЕ СЕЧЕНИЕ В РАСТЕНИЯХ! Золотое сечение-
- 13. РИС. 1 ГЕОМЕТРИЧЕСКОЕ ИЗОБРАЖЕНИЕ ЗОЛОТОЙ ПРОПОРЦИИ Рис.2
- 14. Золотое сечение в растенияхВ природе Золотое сечение
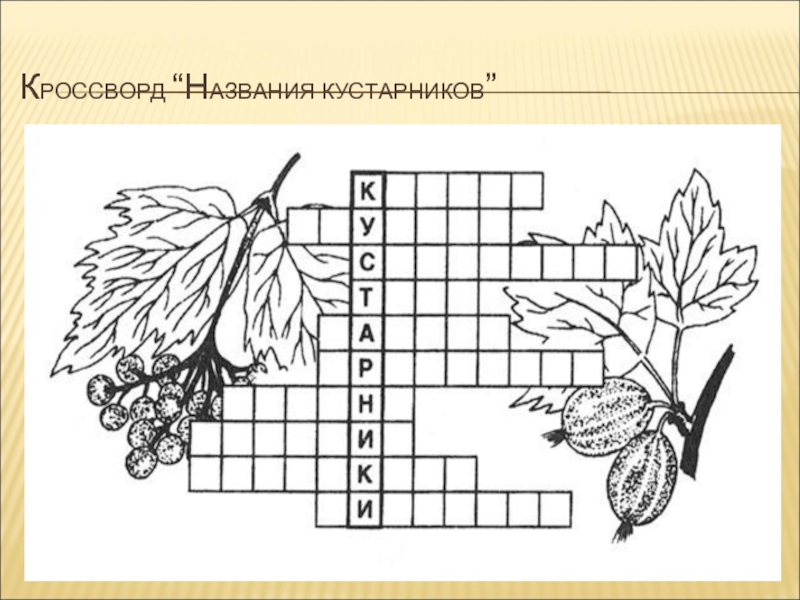
- 15. КРОССВОРД “НАЗВАНИЯ КУСТАРНИКОВ”
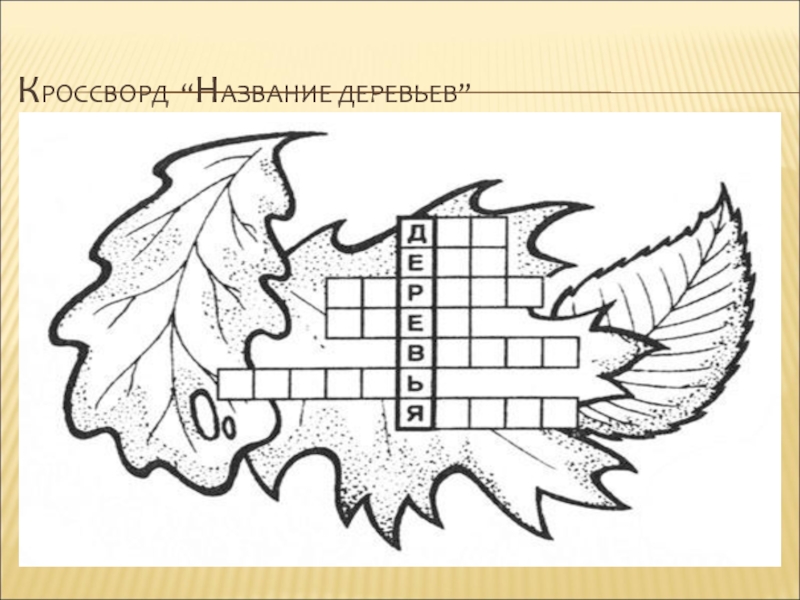
- 16. КРОССВОРД “НАЗВАНИЕ ДЕРЕВЬЕВ”
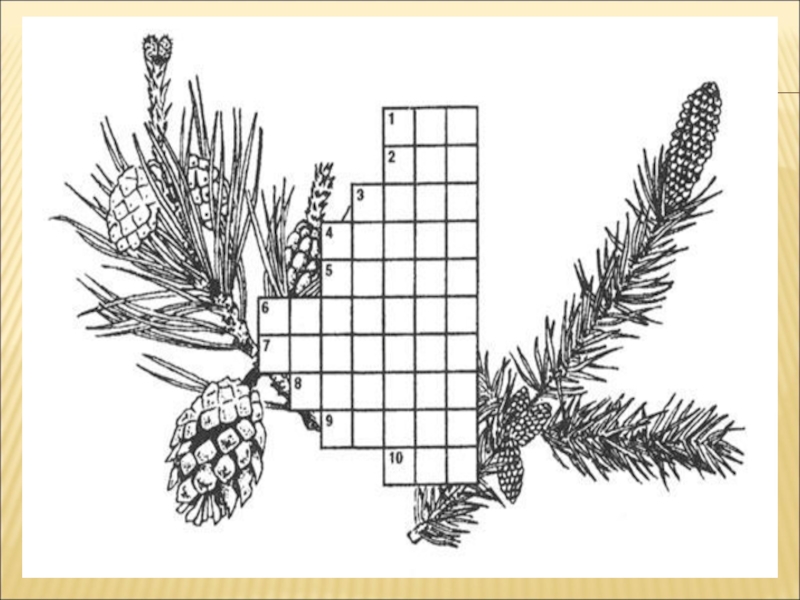
- 17. КРОССВОРД “НАЗВАНИЯ ХВОЙНЫХ РАСТЕНИЙ”1)Дерево с вечнозеленой хвоей.2)Дерево
- 18. Слайд 18
- 19. КРОССВОРД “ДЕРЕВЬЯ И КУСТАРНИКИ”1)Многолетний кустарник с черными
- 20. КРОССВОРД “БУКВА Р”1)Ветвистый кустарник семейства барбарисовых.2)Дерево семейства
- 21. Слайд 21
- 22. РЕБУС “ХВОЙНЫЕ РАСТЕНИЯ”Какое значение имеют хвойные растения в природе?
- 23. РЕБУС “ВОЗДУХ В ХВОЙНОМ ЛЕСУ”Почему воздух в
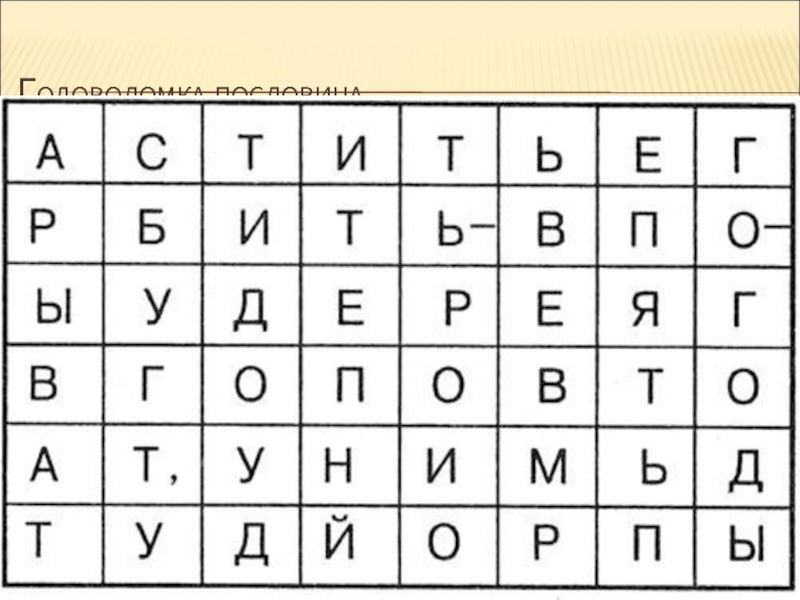
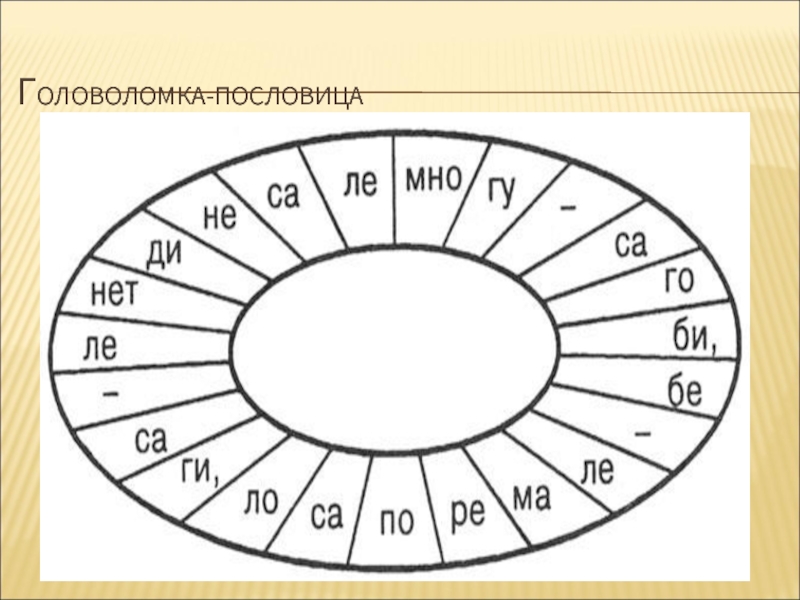
- 24. ГОЛОВОЛОМКА-ПОСЛОВИЦА
- 25. ГОЛОВОЛОМКА-ПОСЛОВИЦА
- 26. ЛАБИРИНТ “СИМБИОЗ”
- 27. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2ЧТО ТАКОЕ СИММЕТРИЯ? КАКИЕ ТОЧКИ НАЗЫВАЮТСЯ СИММЕТРИЧНЫМИ?
Симметрия – это соразмерность,
одинаковость в расположении частей чего-нибудь по противоположным сторонам от точки,
прямой или плоскости.Две точки называются симметричными относительно прямой а, если эта прямая проходит через середину отрезка АА и перпендикулярна к нему. Каждая точка прямой а считается симметричной самой себе.
Слайд 3 СИММЕТРИЯ РАСТЕНИЙ!
На явление
симметрии в
живой природе обратили внимание в Древней
Греции пифагорейцы в связи с развитием ими учения о гармонии. Слайд 4ЦЕНТРАЛЬНАЯ СИММЕТРИЯ.
Фигура называется симметричной относительно точки О, если для каждой
точки фигуры симметричная ей точка относительно точки О также принадлежит
этой фигуре. Точка О называется центром симметрии фигуры. Говорят также, что фигура обладает центральной симметрией.Слайд 5ПРИМЕРЫ ЦЕНТРАЛЬНОЙ СИММЕТРИИ.
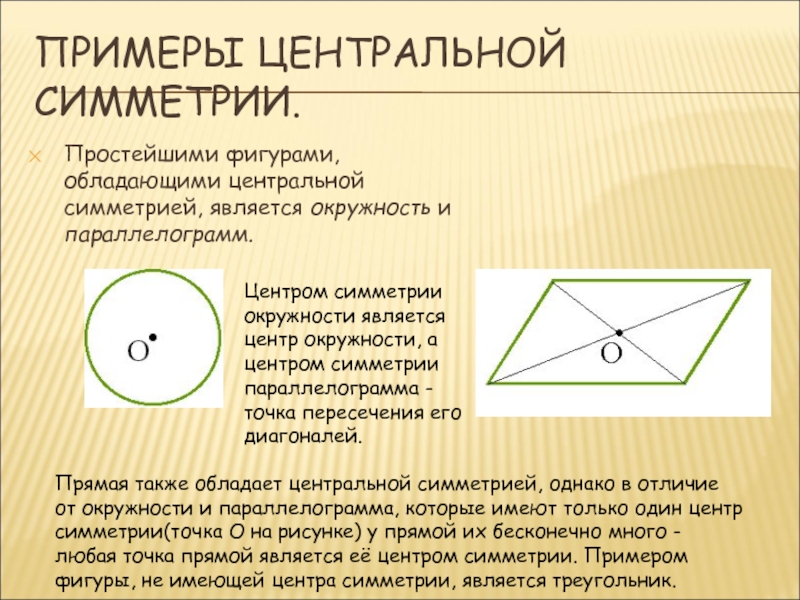
Простейшими фигурами, обладающими центральной симметрией, является окружность и
параллелограмм.
Центром симметрии окружности является центр окружности, а центром симметрии параллелограмма
- точка пересечения его диагоналей. Прямая также обладает центральной симметрией, однако в отличие от окружности и параллелограмма, которые имеют только один центр симметрии(точка О на рисунке) у прямой их бесконечно много - любая точка прямой является её центром симметрии. Примером фигуры, не имеющей центра симметрии, является треугольник.
Слайд 6ЦЕНТРАЛЬНАЯ СИММЕТИРЯ В РАСТЕНИЯХ
Центральную можно наблюдать на изображении следующих цветов:
цветок одуванчика, цветок мать-и-мачехи, цветок кувшинки, сердцевина ромашки, а в
некоторых центральной симметрией обладает и изображение всего цветка ромашки. На данном рисунке представлен подсолнечник.Слайд 7ОСЕВАЯ (ЗЕРКАЛЬНАЯ) СИММЕТРИЯ.
Фигура называется симметричной относительно прямой а, если для
каждой точки фигуры симметричная ей точка относительно прямой а также
принадлежит этой фигуре. Прямая а называется осью симметрии фигуры. Говорят также, что фигура обладает осевой симметрией.На рисунке показан простой пример объекта и его зазеркального двойника – треугольник ABC и треугольник А1В1С1 (здесь MN – пересечение плоскости зеркала с плоскостью рисунка). Каждой точке объекта соответствует определённая точка зазеркального двойника. Эти точки находятся на одном перпендикуляре к прямой MN, по разные стороны и на одинаковом расстоянии от неё. Объект на рисунке выбран для простоты двухмерным. В общем случае объект (и соответственно его зазеркальный двойник) является трёхмерным.
Слайд 8ОСЕВАЯ СИММЕТРИЯ В РАСТЕНИЯХ
В любом растении можно найти какую-то его
часть, обладающую осевой или центральной симметрией. Это могут быть листья,
цветы, стебли, стволы деревьев, плоды, и более мелкие части, такие как сердцевина цветка, пестик, тычинки и другие.Слайд 9ПОВОРОТНАЯ СИММЕТРИЯ.
Предположим, что объект совмещается сам с собой при повороте
вокруг некоторой оси на угол, равный 360°/n (или кратный этой
величине), где n = 2, 3, 4, … В этом случае о поворотной симметрии, а указанную ось называют поворотной осью n-го порядка. Рассмотрим примеры со всеми известными буквами «И» и «Ф». Что касается буквы «И», то у нее есть так называемая поворотная симметрия. Если повернуть букву «И» на 180° вокруг оси, перпендикулярной к плоскости буквы и проходящей через ее центр, то буква совместится сама с собой. Иными словами, буква «И» симметрична относительно поворота на 180°. Заметим, что поворотной симметрией обладает также буква «Ф».На рисунке даны примеры простых объектов с поворотными осями разного порядка – от 2-го до 5-го.
Слайд 10ПОВОРОТНАЯ СИММЕТРИЯ В РАСТЕНИЯХ
Веточка акации имеет зеркальную и поворотную симметрию.
Веточка боярышника обладает скользящей осью симметрии. Гусиная лапчатка имеет поворотную
симметрию и зеркальную.Слайд 11ЧИСЛА ФИБОНАЧЧИ И РАСТЕНИЯ
Последовательности
Фибоначчи (1,1,2,3,5,8,13 и т.д.), где каждое число является
суммой двух предыдущихСлайд 12ЗОЛОТОЕ СЕЧЕНИЕ В РАСТЕНИЯХ!
Золотое сечение- это такое
В математике пропорцией
пропорциональное
деление называют равенство двух отрезка на равные части, при отношений: a:b=c:d.
котором весь отрезок так
относится к большой части,
как сама большая часть
относится к меньшей; или
другими словами, меньший
отрезок так относится к
большому, как больший ко
всему а:b=b:c или c:b=b:a.
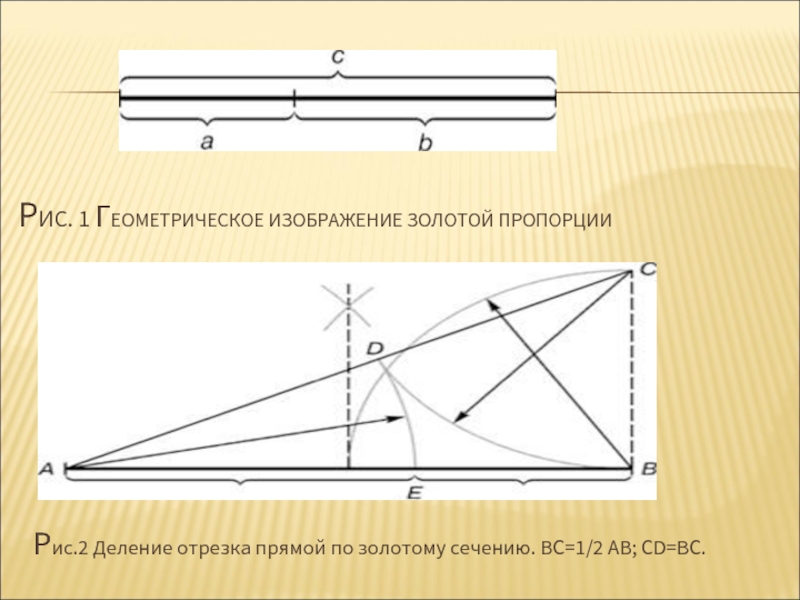
Слайд 13РИС. 1 ГЕОМЕТРИЧЕСКОЕ ИЗОБРАЖЕНИЕ ЗОЛОТОЙ ПРОПОРЦИИ
Рис.2 Деление отрезка прямой
по золотому сечению. ВС=1/2 АВ; CD=ВС.
Слайд 14Золотое сечение в растениях
В природе Золотое сечение появляется с завидной
регулярностью: деревья, растения и цветы вместе с раковинами, бабочками и
дельфинами характеризуются этой пропорцией.
Слайд 17КРОССВОРД “НАЗВАНИЯ ХВОЙНЫХ РАСТЕНИЙ”
1)Дерево с вечнозеленой хвоей.
2)Дерево с твердой древесиной.
3)Дерево
семейство сосновых, распространенное в Сибири.
4)Распространенное хвойное дерево.
5)Крупное дерево семейство сосновых,
распространенное в тайге.6)Дерево с густой пирамидальной крой.
7)Исполин растительного мира, сохранился только в Калифорнии.
Высота некоторых деревьев достигает 150м
8)Дерево семейства араукариевых.
9)Род древесных растений семейства кипарисовых.
10)Кустарник семейства кипарисовых.
Слайд 19КРОССВОРД “ДЕРЕВЬЯ И КУСТАРНИКИ”
1)Многолетний кустарник с черными плодами.
2)Дерево с плодами-орешками.
3)Растение
семейства ивовых, из прутьев которого плетут корзины.
4)Плодовое растение с красными
плодами.5)Небольшое деревце или кустарник семейства розоцветных, родиной которого является Кавказ.
Слайд 20КРОССВОРД “БУКВА Р”
1)Ветвистый кустарник семейства барбарисовых.
2)Дерево семейства розовых, родиной которого
является Тянь-Шань.
3)Кустарник семейства маслиновых, плод-черная овальная ягода.
4)Распространенное дерево, цветки которого
собраны в сережки.5)Небольшое дерево или кустарник из семейства гранатовых, плоды красноватые, с кожистыми околоплодниками.
6)Долговечное дерево Китая и Японии, иначе называется яблоком Востока.
7)Дерево с черными сильновяжущими плодами.
8)Мелкий кустарник семейства брусничных, с черными плодами.
9)Однолетнее растение семейства бобовых, с округло-цилиндричискимя плодами.
10)Дерево семейства розоцветных, с плодами грушевидной или шаровидной формы.
11)Дерево семейства розоцветных, с плодами оранжево-красной окраски.
12)Дерево высотой до 35м из семейства сосновых, с крупными шишками.
13)Дерево из семейства розоцветных, родиной которого считают Китай.