Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Призма и ее свойства
Содержание
- 1. Призма и ее свойства
- 2. Многоугольники A1A2…An и B1B2…Bn называются основаниями призмы,а параллелограммы – боковыми гранями призмы
- 3. Отрезки A1B1, A2B2, … , AnBn называются
- 4. Призму с основаниями A1A2…An и B1B2…Bn обозначают A1A2…AnB1B2…Bn и называют n-угольной призмой
- 5. Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы Высота призмы
- 6. Если боковые ребра призмы перпендикулярны к основаниям,
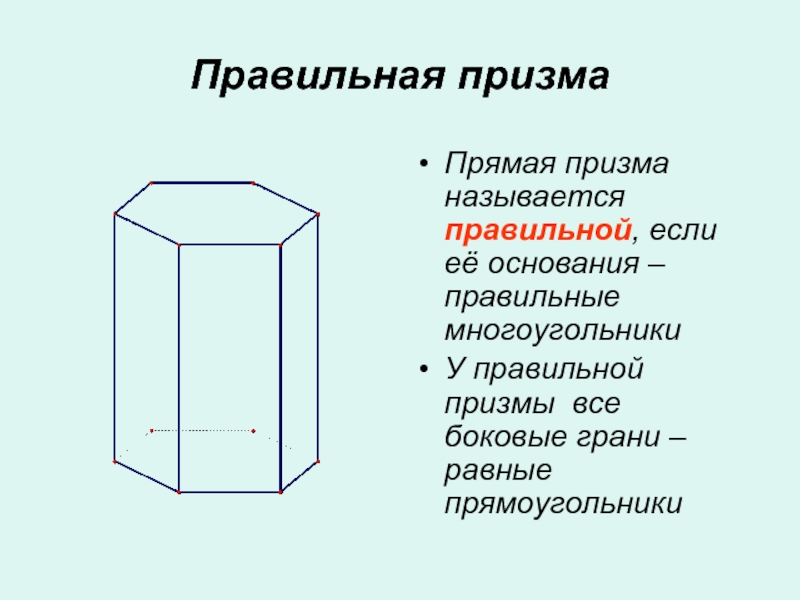
- 7. Правильная призмаПрямая призма называется правильной, если её
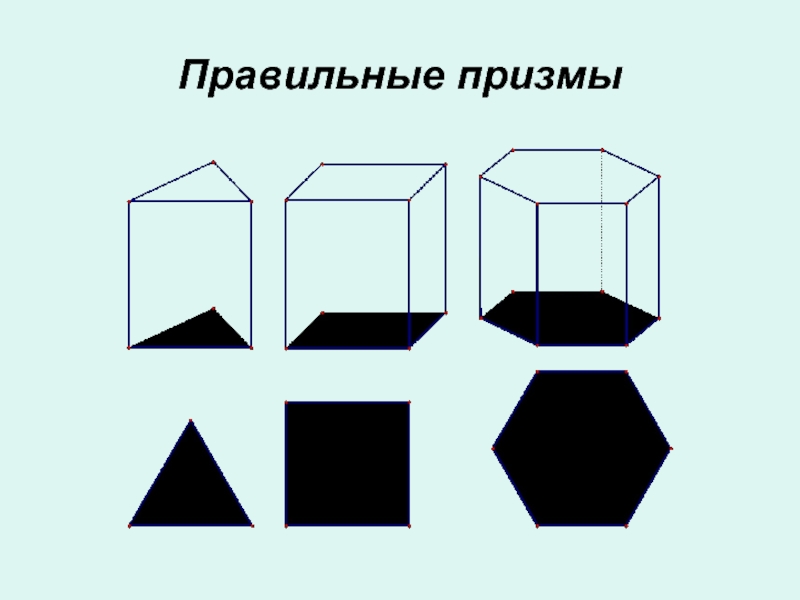
- 8. Правильные призмы
- 9. ПараллелепипедЕсли основания призмы - параллелограммы, то призма является параллелепипедомВ параллелепипеде все грани являются параллелограммами
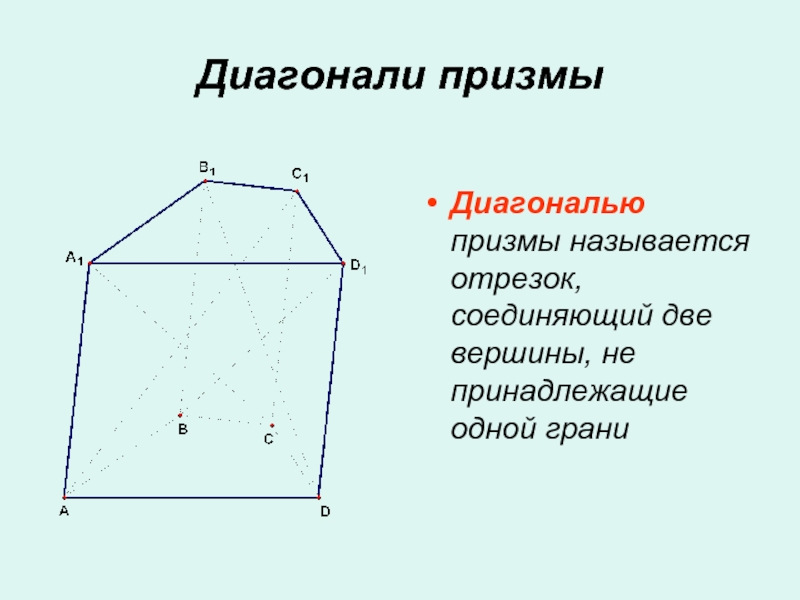
- 10. Диагонали призмыДиагональю призмы называется отрезок, соединяющий две вершины, не принадлежащие одной грани
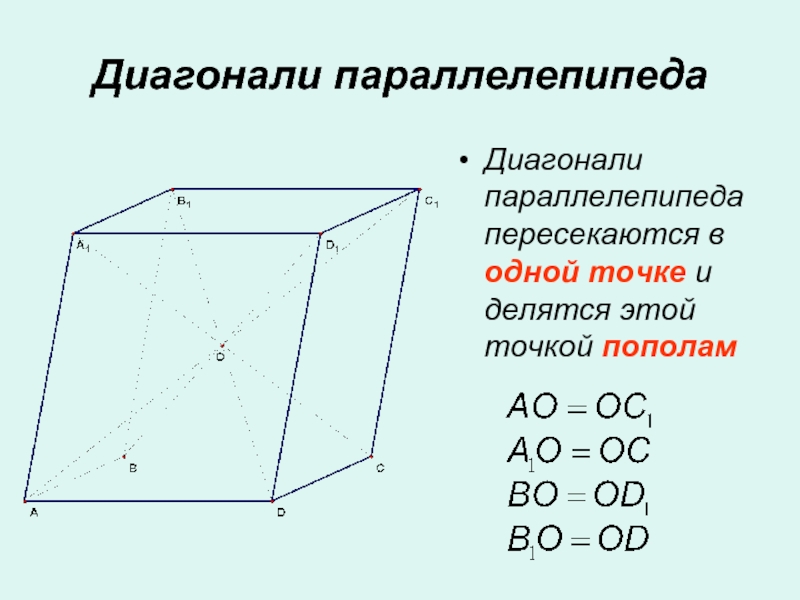
- 11. Диагонали параллелепипедаДиагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам
- 12. Диагональные сечения призмыСечения призмы плоскостями, проходящими через
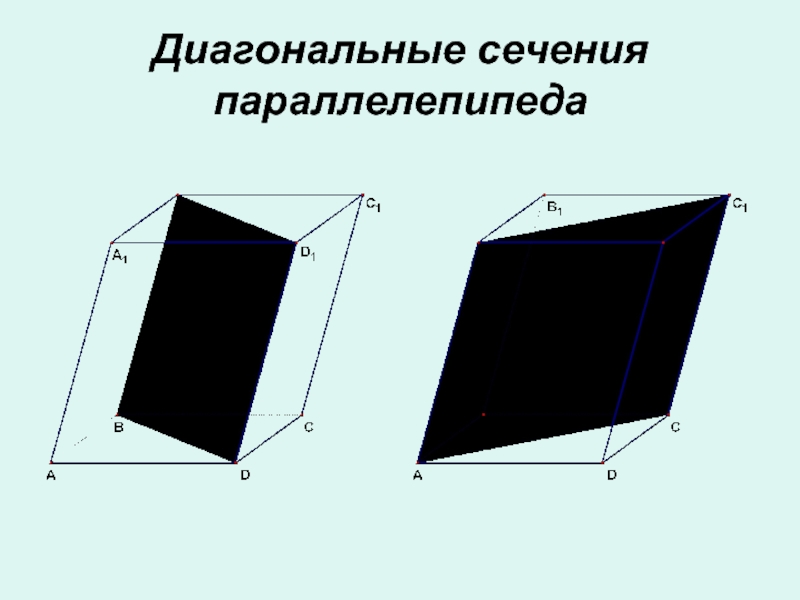
- 13. Диагональные сечения параллелепипеда
- 14. Площадь поверхности призмыПлощадью полной поверхности призмы называется
- 15. Теорема о площади боковой поверхности прямой призмы Теорема.
- 16. Доказательство теоремыБоковые грани прямой призмы – прямоугольники,
- 17. Слайд 17
- 18. Скачать презентанцию
Многоугольники A1A2…An и B1B2…Bn называются основаниями призмы,а параллелограммы – боковыми гранями призмы
Слайды и текст этой презентации
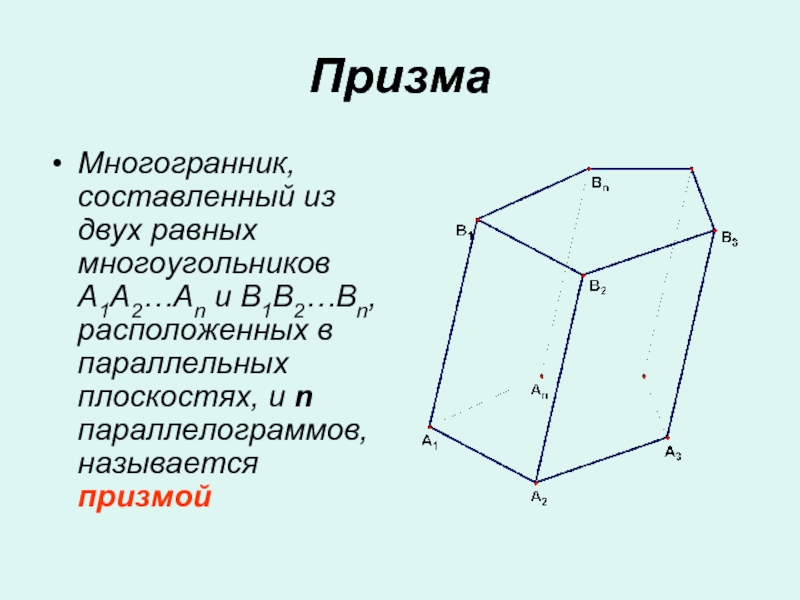
Слайд 1Призма
Многогранник, составленный из двух равных многоугольников A1A2…An и B1B2…Bn, расположенных
в параллельных плоскостях, и n параллелограммов, называется призмой
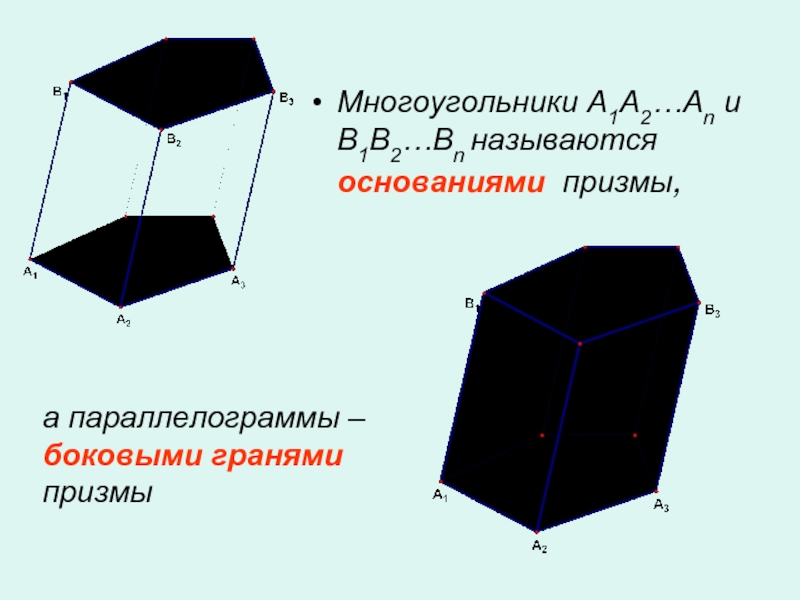
Слайд 2Многоугольники A1A2…An и B1B2…Bn называются основаниями призмы,
а параллелограммы – боковыми
гранями призмы
Слайд 3Отрезки A1B1, A2B2, … , AnBn называются боковыми ребрами призмы
Боковые
ребра призмы равны и параллельны
Боковые ребра призмы
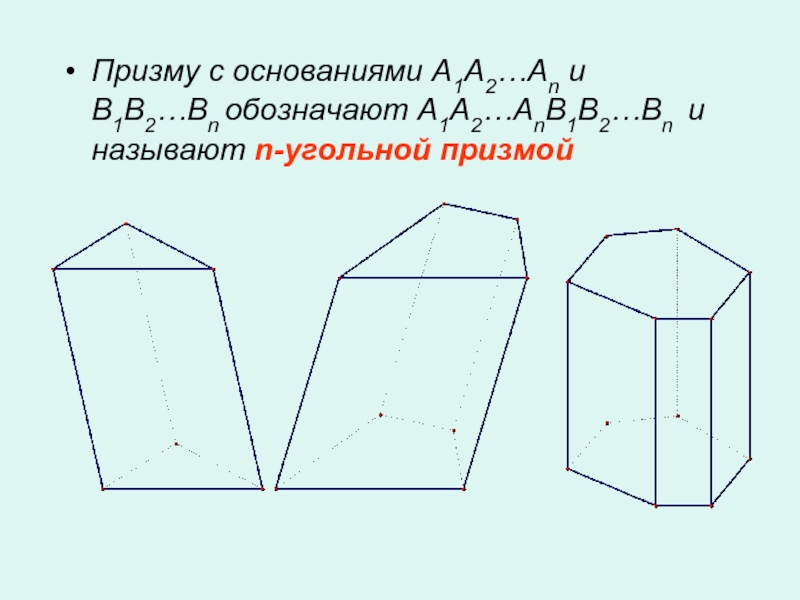
Слайд 4Призму с основаниями A1A2…An и B1B2…Bn обозначают A1A2…AnB1B2…Bn и называют
n-угольной призмой
Слайд 5Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого
основания, называется высотой призмы
Высота призмы
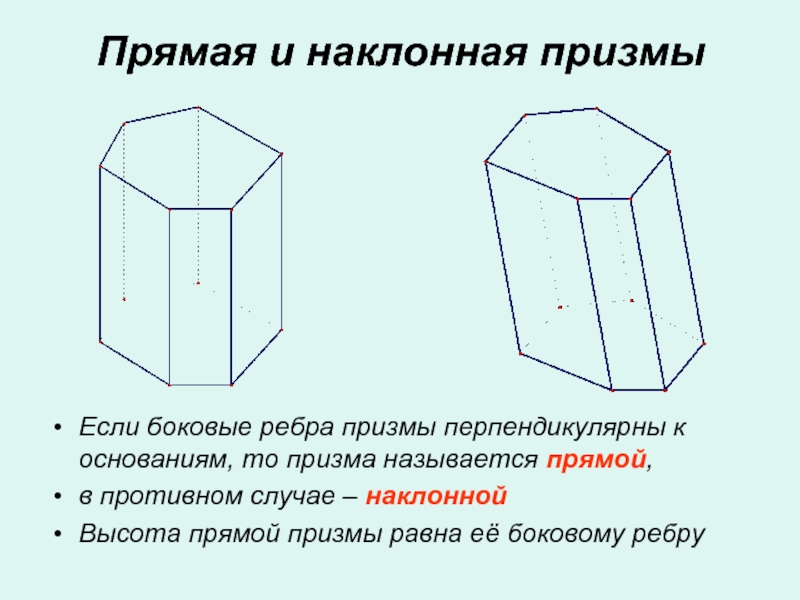
Слайд 6Если боковые ребра призмы перпендикулярны к основаниям, то призма называется
прямой,
в противном случае – наклонной
Высота прямой призмы равна её
боковому ребруПрямая и наклонная призмы
Слайд 7Правильная призма
Прямая призма называется правильной, если её основания – правильные
многоугольники
У правильной призмы все боковые грани – равные прямоугольники
Слайд 9Параллелепипед
Если основания призмы - параллелограммы, то призма является параллелепипедом
В параллелепипеде
все грани являются параллелограммами
Слайд 10Диагонали призмы
Диагональю призмы называется отрезок, соединяющий две вершины, не принадлежащие
одной грани
Слайд 11Диагонали параллелепипеда
Диагонали параллелепипеда пересекаются в одной точке и делятся этой
точкой пополам
Слайд 12Диагональные сечения призмы
Сечения призмы плоскостями, проходящими через два боковых ребра,
не принадлежащих одной грани, называются диагональными сечениями
Диагональные сечения призмы являются
параллелограммамиСлайд 14Площадь поверхности призмы
Площадью полной поверхности призмы называется сумма площадей всех
её граней
Площадью боковой поверхности призмы называется сумма площадей её боковых
гранейСлайд 15Теорема о площади боковой поверхности прямой призмы
Теорема.
Площадь боковой поверхности
прямой призмы равна произведению периметра основания на высоту призмы
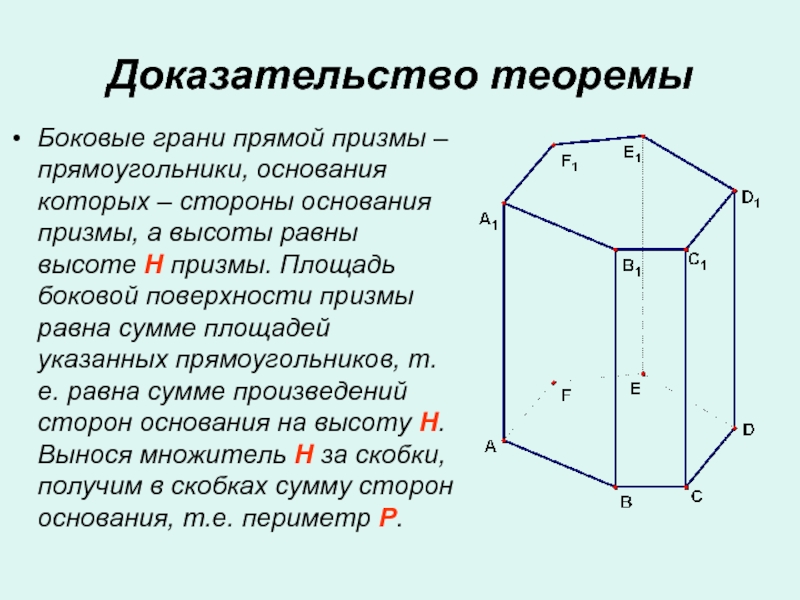
Слайд 16Доказательство теоремы
Боковые грани прямой призмы – прямоугольники, основания которых –
стороны основания призмы, а высоты равны высоте H призмы. Площадь
боковой поверхности призмы равна сумме площадей указанных прямоугольников, т.е. равна сумме произведений сторон основания на высоту H. Вынося множитель H за скобки, получим в скобках сумму сторон основания, т.е. периметр P.
Теги