Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация по теме "Треугольник. Свойство его сторон и углов"
Содержание
- 1. Презентация по теме "Треугольник. Свойство его сторон и углов"
- 2. Треугольник — геометрическая фигура, образованная тремя отрезками, которые соединяют три точки,
- 3. Равнобедренный треугольник.Равнобедренный треугольник — это треугольник, в котором две
- 4. Правильный (или равносторонний) треугольник.Правильный (или равносторонний) треугольник — это правильный многоугольник с тремя сторонами, первый из
- 5. Слайд 5
- 6. Медиана. Отрезок, соединяющий вершину треугольника с серединой противоположной стороны треугольника, называется медианой треугольника.
- 7. Свойства точек пересечения медиан. Медианы треугольника пересекаются
- 8. Биссектриса.Биссектрисой треугольника называют отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой на противолежащей стороне.
- 9. Прямоуго́льный треуго́льник.Прямоуго́льный треуго́льник — это треугольник, в котором один угол прямой (то
- 10. Слайд 10
- 11. Внешний угол треугольника.Внешний угол треугольника при данной вершине — это угол, смежный с внутренним углом треугольника при этой вершине.
- 12. Как построить внешний угол треугольника? Нужно продлить
- 13. Спасибо за внимание!
- 14. Скачать презентанцию
Треугольник — геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Указанные три точки называются вершинами треугольника, а отрезки — сторонами треугольника. Стороны треугольника образуют в вершинах треугольника три угла. Другими словами, треугольник — это многоугольник, у которого
Слайды и текст этой презентации
Слайд 2Треугольник — геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на
Слайд 3Равнобедренный треугольник.
Равнобедренный треугольник — это треугольник, в котором две стороны равны между
собой по длине. Боковыми называются равные стороны, а последняя — основанием.
По определению, правильный треугольник также является равнобедренным, но обратное утверждение неверно.Слайд 4Правильный (или равносторонний) треугольник.
Правильный (или равносторонний) треугольник — это правильный многоугольник с тремя сторонами, первый из правильных многоугольников. Все стороны правильного треугольника равны
между собой, а все углы также равны и составляют 60°. В
равностороннем треугольнике высота является и биссектрисой, и медианой.Слайд 6Медиана.
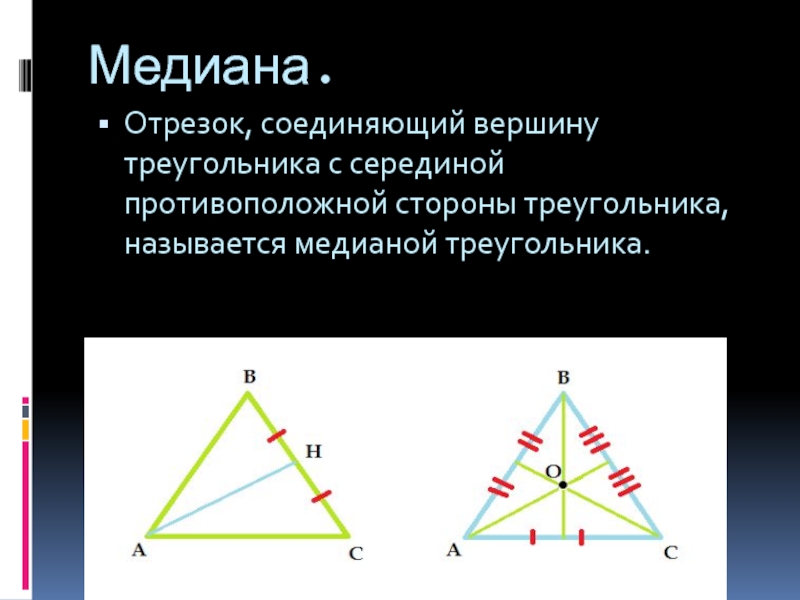
Отрезок, соединяющий вершину треугольника с серединой противоположной стороны треугольника,
называется медианой треугольника.
Слайд 7Свойства точек пересечения медиан.
Медианы треугольника пересекаются в одной точке, которая называется центром
тяжести треугольника, и делятся этой точкой на две части в отношении
2:1, считая от вершины.Внутренняя медиана угла треугольника сопряжена самой себе.
Слайд 8Биссектриса.
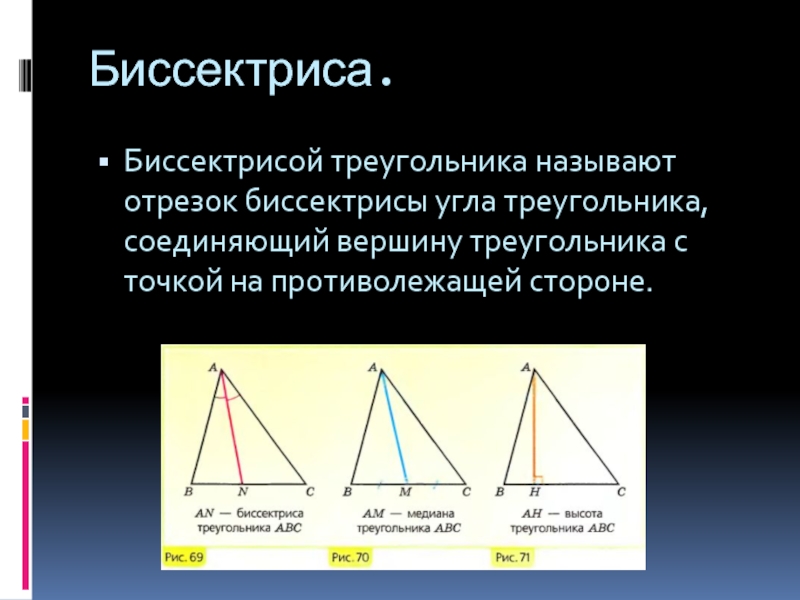
Биссектрисой треугольника называют отрезок биссектрисы угла треугольника, соединяющий вершину треугольника
с точкой на противолежащей стороне.
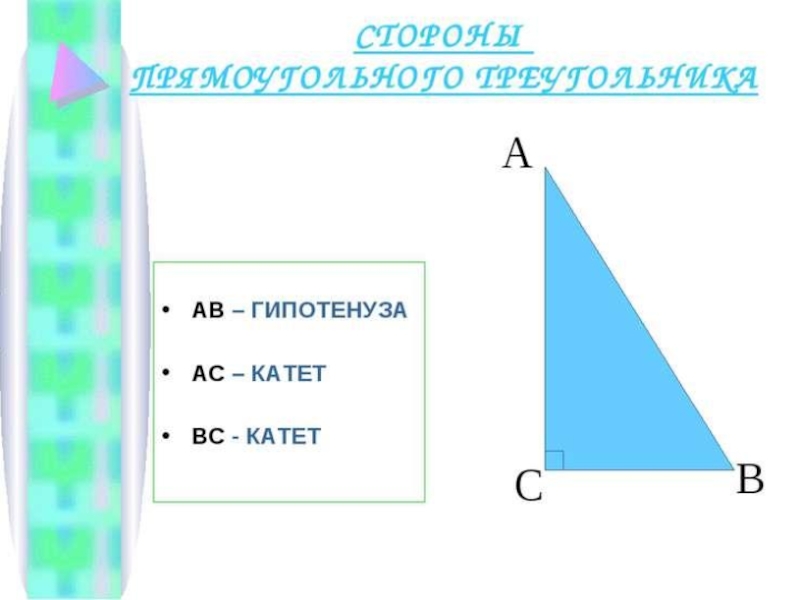
Слайд 9Прямоуго́льный треуго́льник.
Прямоуго́льный треуго́льник — это треугольник, в котором один угол прямой (то есть составляет 90 градусов).
Соотношения
между сторонами и углами прямоугольного треугольника лежат в основе тригонометрии.
Слайд 11Внешний угол треугольника.
Внешний угол треугольника при данной вершине — это угол, смежный с
внутренним углом треугольника при этой вершине.
Слайд 12Как построить внешний угол треугольника? Нужно продлить сторону треугольника.
На рисунке:
∠3
— внешний угол при вершине А,
∠2 — внешний угол при
вершине С,∠1 — внешний угол при вершине В.
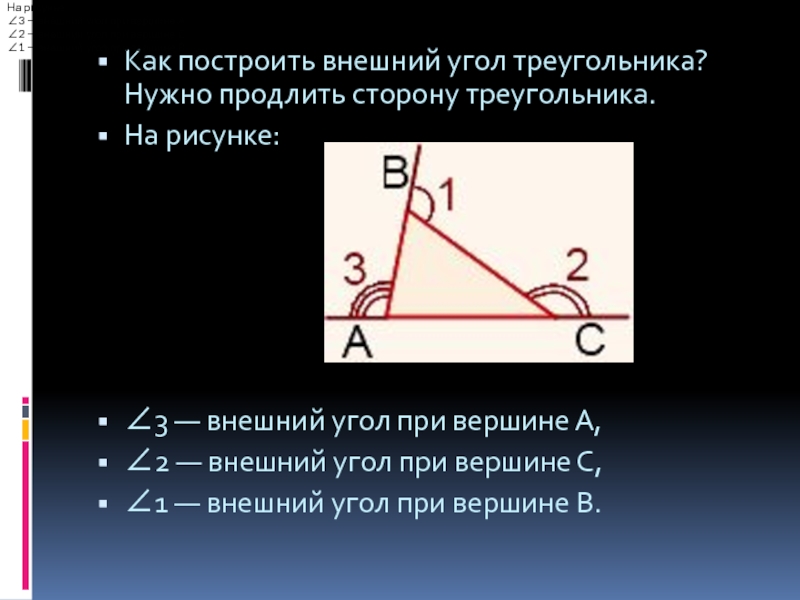
Как построить внешний угол треугольника? Нужно продлить сторону треугольника.
На рисунке:
∠3 — внешний угол при вершине А,
∠2 — внешний угол при вершине С,
∠1 — внешний угол при вершине В.