Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математика. Презентация" №11. Профильный уровень. Задачи на смеси и сплавы"
Содержание
- 1. Математика. Презентация" №11. Профильный уровень. Задачи на смеси и сплавы"
- 2. Имеются два сосуда. Первый
- 3. Вспомним, что процентное содержание выражается формулой:Чтобы решить
- 4. Имеются два сосуда. Первый
- 5. 2 случай . Возьмем равные массы
- 6. Составим систему уравненийX = 1254 -1206X = 4848 кг кислоты содержится в первом сосуде
- 7. Смешав 77-процентный и 79-процентный растворы кислоты
- 8. Т.к. получили 70-процентный раствор кислоты, составим первое
- 9. Составим систему уравнений:2
- 10. 7∙(125 - 2у) + 9у = 700875
- 11. Смешав 30-процентный и 60-процентный растворы кислоты
- 12. Занесем в таблицу условие задачи. Составим первое
- 13. Слайд 13
- 14. Составим систему уравнений:(-6)
- 15. -11 (4y – 60) +19y = -90-44y
- 16. Скачать презентанцию
Имеются два сосуда. Первый содержит 100 кг, а второй — 90 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 66% кислоты.
Слайды и текст этой презентации
Слайд 2 Имеются два сосуда. Первый содержит 100 кг,
а второй — 90 кг раствора кислоты различной концентрации. Если
эти растворы смешать, то получится раствор, содержащий 66% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 67% кислоты.Сколько килограммов кислоты содержится в первом сосуде?
№11
Слайд 3Вспомним, что процентное содержание выражается формулой:
Чтобы решить эту задачу нужно
составить систему уравнений, составив перед этим таблицу
Слайд 4 Имеются два сосуда. Первый содержит 100 кг,
а второй — 90 кг раствора кислоты различной концентрации. Если
эти растворы смешать, то получится раствор, содержащий 66% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 67% кислоты. Сколько килограммов кислоты содержится в первом сосуде?Решение
Пусть х кг кислоты содержится в первом сосуде,
а y кг кислоты содержится во втором сосуде,
тогда (x + y) кг – масса кислоты в первом растворе,
И масса первого раствора будет:
100 + 90 = 190 (кг)
Т.К получится раствор, содержащий 66% кислоты, то составим 1 уравнение:
№11
Слайд 52 случай .
Возьмем равные массы двух веществ.
Берем максимальную
величину меньшего по
массе раствора ( 90 кг ) и равную
величину меньшегопо массе раствора от первого: от 100 кг берем 90 кг
т.к. второй раствор весит 90 кг
90 + 90 = 180(кг) - масса нового раствора
(0,9x + y) кг– масса кислоты
Т.К получится раствор, содержащий 67% кислоты, то составим 2 уравнение:
Слайд 7 Смешав 77-процентный и 79-процентный растворы кислоты и добавив 10
кг чистой воды, получили 70-процентный раствор кислоты.
Если бы вместо 10 кг воды добавили 10 кг 50- процентного раствора той же кислоты, то получили бы 75-процентный раствор кислоты. Сколько килограммов 77-процентного раствора использовали для получения смеси?№11
Решение
Пусть х кг будет масса первого раствора, а масса чистого вещества будет 0,77х (по условию)
Масса второго вещества пусть будет у кг, а масса чистого вещества будет 0,79у (по условию)
Так как эти два раствора перелили в один общий сосуд и добавили еще 10 кг чистой воды то общая масса всего раствора: (x+y+10) кг
Слайд 8Т.к. получили 70-процентный раствор кислоты, составим первое уравнение системы:
Рассмотрим 2
случая
По условию сказано, что если бы вместо 10 кг воды
добавили 10 кг 50%раствора той же кислоты, то получили бы 75% раствор кислотыСоставим второе уравнение системы:
Слайд 107∙(125 - 2у) + 9у = 700
875 - 14у +
9у = 700
- 5у = -175
у = 35
х =
125 - 2∙35 х = 55
55 кг -77-процентного раствора
В ответе нужно записать, сколько килограммов 77% раствора использовали для получения смеси, то есть X:
Слайд 11 Смешав 30-процентный и 60-процентный растворы кислоты и добавив 10
кг чистой воды, получили
36-процентный раствор кислоты.Если бы вместо 10 кг воды добавили 10 кг 50- процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты.
Сколько килограммов 30-процентного раствора использовали для получения смеси?
№11
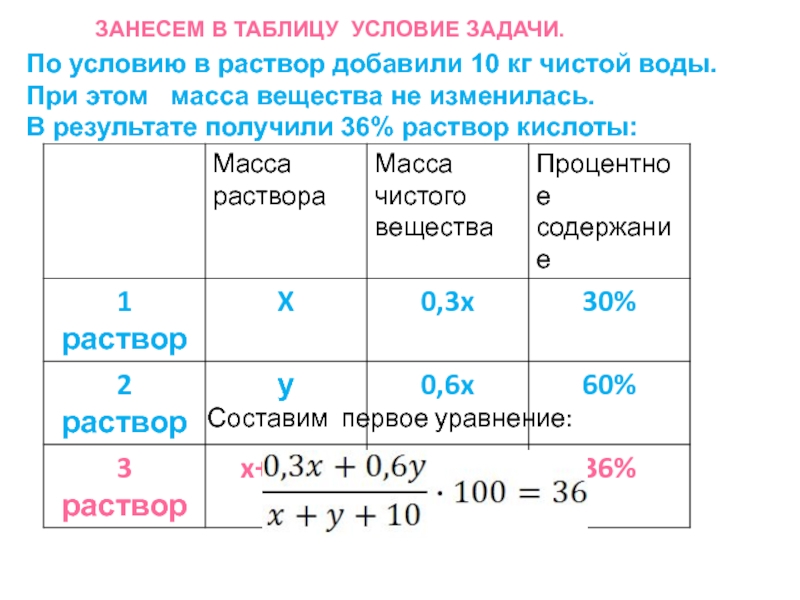
Слайд 12Занесем в таблицу условие задачи.
Составим первое уравнение:
По условию в раствор
добавили 10 кг чистой воды. При этом масса вещества
не изменилась. В результате получили 36% раствор кислоты:
Слайд 13
Если бы вместо 10 кг добавили 10 кг 50% раствора
той же кислоты то получили бы 41% раствор кислоты
Составим второе
уравнение
Слайд 15-11 (4y – 60) +19y = -90
-44y + 660 +19y
= -90
-25y = -750
y = 30
В ответе нужно записать, сколько
килограммов 30% раствора использовали для получения смеси, то есть X:X = 4∙30 – 60 = 60
