Математика. Презентация" №16.Цилиндр. Базовый уровень"

цилиндрический сосуд налили 2000 см²  воды. Уровень воды при этом достигает

Объём вытесненной жидкости равен 9/12 исходного объёма:

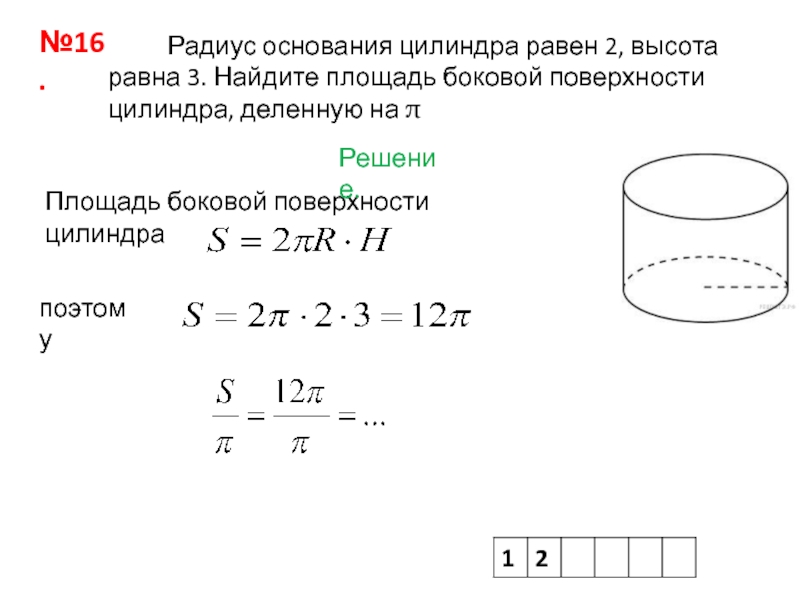
№16.

Решение.

Объём детали равен объёму вытесненной ею жидкости.

котором находится 6 литров воды, опущена деталь. При этом уровень

№16.

Решение.

Объём вытесненной жидкости равен 1/2 исходного объёма:

Объём детали равен объёму вытесненной ею жидкости.

сосуде уровень жидкости достигает 16 см. На какой высоте будет

№16.

Решение.

Отсюда высота

Число π — это величина постоянная, объем жидкости
V в данной задаче тоже не изменяется.

То есть, высота уровня жидкости обратно пропорциональна радиусу основания сосуда.

Так как радиус увеличился в 2 раза, то высота уменьшится в 4 раза. (  2²= 4 )

сосуде уровень жидкости достигает 16 см. На какой высоте будет

Объем цилиндрического сосуда, зная его диаметр и высоту находится по формуле:

При увеличении диаметра сосуда в 2 раза высота равного объема жидкости 

уменьшится в 4 раза и станет равна 4.

№16.

Решение.

второго цилиндра высота в три раза больше, а радиус основания —

Пусть объём первого цилиндра равен 

объём второго 

где R₁ R₂ — радиусы оснований цилин­дров,  H₁ H₂ — их высоты.

то выразим объём второго цилиндра через объём первого:

№16.

Решение.

Т.к.

равен 12 м3. У второго цилиндра высота в три раза

Объем цилиндра вычисляется по формуле V = πR²H,
где R - радиус основания, H - высота цилиндра.

Тогда

Ответ: 9

№16.

Решение.

Из условий задачи :

выше второй, зато вторая в полтора раза шире. Найдите отношение

№16.

Решение.

Т.к.

Пусть объёмы первой и второй кружек равны 

кружка в полтора раза ниже второй, а вторая вдвое шире

№16.

Решение.

Т.к.

Пусть объёмы первой и второй кружек равны 

кружка вдвое выше второй, а вторая в четыре раза шире

Решение.

Т.к.

Пусть объёмы первой и второй кружек равны 

высота равна 3. Найдите площадь боковой поверхности цилиндра, деленную на π
Площадь

поэтому

№16.

Решение.

основания цилиндра равна 3, высота равна 2. Найдите площадь боковой

Длина окружности основания цилиндра равна 3. Площадь боковой поверхности равна 6. Найдите высоту цилиндра.

№16.

Решение.

Решение.

Площадь боковой поверхности цилиндра  

C– длина окружности основания.

Поэтому  S = 2·3 = 6

№16.

цилиндра равна 2π, а высота — 1. Найдите диаметр основания.
№16.
Решение.

Площадь боковой поверхности цилиндра  

№16.

налито 5 л воды. После полного погружения в воду детали,

№16.

Решение.

Объём детали равен объёму вытесненной ею жидкости.

После погружения детали в воду объём стал равен
5 · 1,2 = 6 литров,

поэтом объём детали равен 6 − 5 = 1 л = 1000 см3.

сосуде цилиндрической формы находится на уровне  h = 40cм.

Объём воды, налитой в цилиндр, высотой  h и радиусом R равен 
V = πR²h

№16.

Решение.

Следовательно, при увеличении радиуса цилиндра в 2 раза, при неизменном объёме,

значит, вода во втором цилиндре достигнет уровня
h₂= 40 : 4= 10 см.

высота стола воды окажется в 2²= 4 раза меньше,

налили воду до уровня 80 см. Какого уровня достигнет вода,

№16.

Решение.

Объём воды, налитой в цилиндр, высотой  h и радиусом R равен 
V = πR²h

Следовательно, при увеличении радиуса цилиндра в 4 раза, при неизменном объёме,

значит, вода во втором цилиндре достигнет уровня
h₂= 80 : 16 = 5 см.

высота стола воды окажется в 4²= 16 раза меньше,