Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математика в изобразительном искусстве
Содержание
- 1. Математика в изобразительном искусстве
- 2. Исторически, математика играла важную роль в изобразительном
- 3. Голландский художник М.К. Эшер (1898-1972) в некотором
- 4. Слайд 4
- 5. МНОГОГРАННИКИ Многогранник - это трехмерное тело, гранями
- 6. ТЕССЕЛЛЯЦИИ Тесселляции, известные также как покрытие плоскости
- 7. HOLLISTER DAVID "СЕМЬ ПТИЦ". НА ЭТОЙ КАРТИНЕ
- 8. ROBERT FATHAUER "ФРАКТАЛЬНЫЕ РЫБЫ - СГРУППИРОВАННЫЕ ГРУППЫ".
- 9. ИСКАЖЕННЫЕ И НЕОБЫЧНЫЕ ПЕРСПЕКТИВЫ Необычные системы перспективы,
- 10. НЕВОЗМОЖНЫЕ ФИГУРЫ Невозможные фигуры - эти фигура,
- 11. ЛЕНТА МЕБИУСА Лента Мебиуса - это трехмерный
- 12. ФРАКТАЛЫ Фрактал - это объект, повторяющий сам
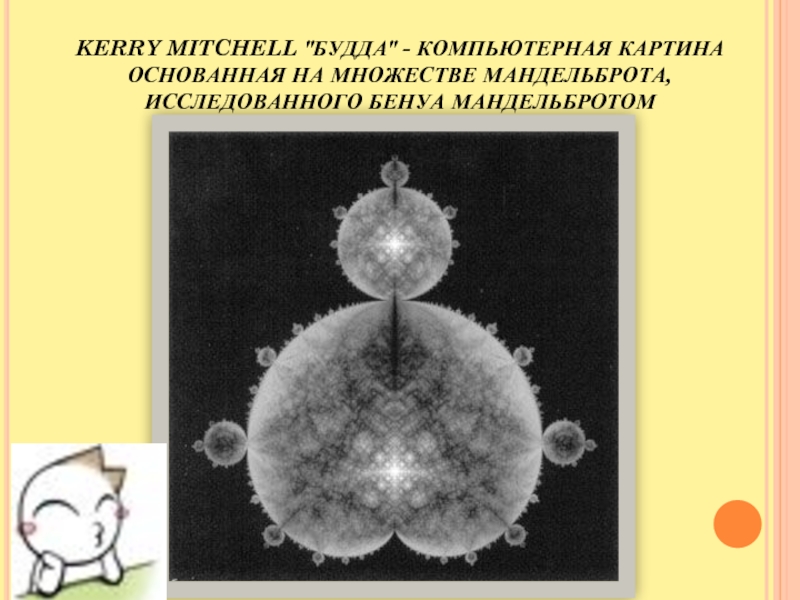
- 13. KERRY MITCHELL "БУДДА" - КОМПЬЮТЕРНАЯ КАРТИНА ОСНОВАННАЯ НА МНОЖЕСТВЕ МАНДЕЛЬБРОТА, ИССЛЕДОВАННОГО БЕНУА МАНДЕЛЬБРОТОМ
- 14. ROBERT FATHAUER "КОМПОЗИЦИЯ КРУГОВ" (2001) - НЕ
- 15. СВЯЗЬ МАТЕМАТИКИ И ИЗОБРАЗИТЕЛЬНОГО ИСКУССТВА ПРИ КОНСТРУКТИВНОМ
- 16. ВазаПри построении в первую очередь учитывается отношение
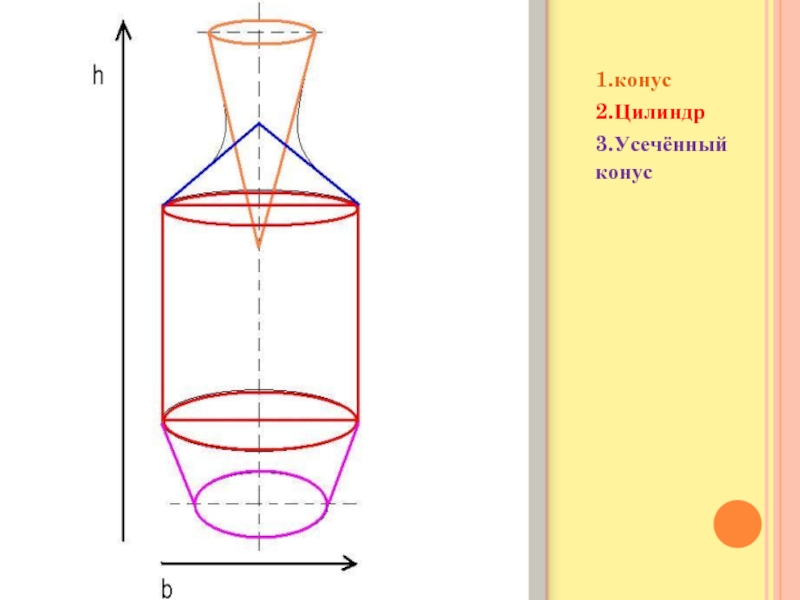
- 17. 1.конус 2.Цилиндр3.Усечённый конус
- 18. То же самое проделывается и в отношении
- 19. КРУЖКА:
- 20. Соединяем три элемента . При этом мы
- 21. МНОГИЕ ХУДОЖНИКИ В СВОИХ РАБОТАХ ИСПОЛЬЗУЮТ МАТЕМАТИКУ.
- 22. Скачать презентанцию
Исторически, математика играла важную роль в изобразительном искусстве, в частности при изображении перспективы, подразумевающем реалистичное изображение трехмерной сцены на плоском холсте или листе бумаги. Согласно современным взглядам, математика и изобразительное искусство
Слайды и текст этой презентации
Слайд 1« МАТЕМАТИКА В ИЗОБРАЗИТЕЛЬНОМ ИСКУССТВЕ» ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА ПО МАТЕМАТИКЕ УЧЕНИЦЫ 10
КЛАССА «А»
СРЕДНЕЙ ШКОЛЫ № 19
ГАЛИТА АНАСТАСИИ
Слайд 2Исторически, математика играла важную роль в изобразительном искусстве, в частности
при изображении перспективы, подразумевающем реалистичное изображение трехмерной сцены на плоском
холсте или листе бумаги. Согласно современным взглядам, математика и изобразительное искусство очень удаленные друг от друга дисциплины, первая - аналитическая, вторая - эмоциональная. Математика не играет очевидной роли в большинстве работ современного искусства, и, фактически, многие художники редко или вообще никогда не используют даже использование перспективы. Однако, есть много художников, у которых математика находится в центре внимания. Несколько значительных фигур в изобразительном искусстве проложили дорогу этим индивидуумам.Слайд 3
Голландский художник М.К. Эшер (1898-1972) в некотором роде является отцом
математического искусства. Математические идеи играют центральную роль в большинстве его
картин за исключением лишь ранних работ. Большинство идей, часто используемых современными математическими художниками, были использованы Эшером, и его работы часто являются источником вдохновения для современных авторов.Слайд 5МНОГОГРАННИКИ
Многогранник - это трехмерное тело, гранями которого являются многоугольники. Существует
всего пять правильных многогранников, у которых все стороны являются правильными
многоугольниками и все вершины одинаковы. Они известны как многоугольники Платона или Платоновы тела. Также существует 13 выпуклых многогранников, гранями которых являются один, два или три правильных многоугольника, и у которых все вершины одинаковы. Они известны как тела Архимеда. Кроме этого существует бесконечное множество призм и антипризм с гранями в виде правильных многоугольников. Эшер использовал многогранники во многих своих работах, включая "Рептилии" (1949), "Двойной планетоид" (1949) и "Гравитация" (1952).Слайд 6ТЕССЕЛЛЯЦИИ
Тесселляции, известные также как покрытие плоскости плитками, являются коллекциями фигур,
которые покрывают всю математическую плоскость, совмещаясь друг с другом без
наложений и пробелов. Правильные тесселляции состоят из фигур в виде правильных многоугольников, при совмещении которых все углы имеют одинаковую форму. Существует всего три многоугольника, пригодные для использования в правильных тесселляциях. Это - правильный треугольник, квадрат и правильный шестиугольник. Полуправильными тесселляциями называют такие тесселляции, в которых использованы правильные многоугольники двух или трех типов и все вершины одинаковы. Существует всего 8 полуправильных тесселляций. Вместе три правильных тесселляции и восемь полуправильных носят название Архимедовых. Тесселляции, в которых отдельные плитки являются узнаваемыми фигурами, являются одной из основных тем творчества Эшера. В его записных книгах содержатся более 130 вариантов тесселляций.Он использовал их в огромном количестве своих картин, среди которых "День и ночь" (1938), серия картин "Предел круга" I-IV, и знаменитые "Метаморфозы" I-III (1937-1968). Примеры ниже - картины современных авторов Холлистера Девида и Роберта Фатауэра.Слайд 7HOLLISTER DAVID "СЕМЬ ПТИЦ". НА ЭТОЙ КАРТИНЕ ИЗОБРАЖЕНЫ СЕМЬ ПТИЦ,
ДВЕ ИЗ КОТОРЫХ ИЗОБРАЖЕНЫ В НЕГАТИВЕ НА ФОНЕ ЛАНДШАФТА ГОРОДА
АХО В АРИЗОНЕ. ПОСЛЕДОВАТЕЛЬНО УМЕНЬШАЮЩИЕСЯ ФИГУРЫ ПТИЦ СОВМЕЩАЮТСЯ ДРУГ С ДРУГОМ В ВИДЕ ФРАКТАЛЬНОЙ ТЕССЕЛЛЯЦИИ. ХВОСТОВЫЕ ПЕРЬЯ КАЖДОЙ ПТИЦЫ ЯВЛЯЮТСЯ РАЗДЕЛЯЮТ КОНСТРУКЦИЮ НАПОПОЛАМ, ОТСЕКАЯ ПРИМЕРНО ТРЕТЬ РАССТОЯНИЯ МЕЖДУ КОНЧИКАМИ КРЫЛЬЕВ. КАЖДАЯ МЕНЬШАЯ ПТИЦА В СВОЮ ОЧЕРЕДЬ ДЕЛИТ СВОЮ ОБЛАСТЬ АНАЛОГИЧНЫМ ОБРАЗОМ. ЕСЛИ ЭТОТ ПРОЦЕСС ПРОДОЛЖАТЬ ДО БЕСКОНЕЧНОСТИ, ПОЛУЧИТСЯ НАБОР ТОЧЕК, ИЗВЕСТНЫЙ КАК МНОЖЕСТВО КАНТОРА ИЛИ КАНТОРОВА ПЫЛЬ.Слайд 8ROBERT FATHAUER "ФРАКТАЛЬНЫЕ РЫБЫ - СГРУППИРОВАННЫЕ ГРУППЫ". ЭТО КОМПЬЮТЕРНАЯ РАБОТА,
РАСПЕЧАТАННАЯ НА ФОТОБУМАГЕ. СКВОЗЬ ИЛЛЮМИНАТОР ВИДНЫ ВОЛНЫ, НО ПРИ БЛИЖАЙШЕМ
РАССМОТРЕНИИ ВИДНО, ЧТО ВОЛНЫ ЯВЛЯЮТСЯ НА САМОМ ДЕЛЕ ФРАКТАЛЬНОЙ ТЕССЕЛЛЯЦИЕЙ, СОСТОЯЩЕЙ ИЗ РЫБ.Слайд 9ИСКАЖЕННЫЕ И НЕОБЫЧНЫЕ ПЕРСПЕКТИВЫ
Необычные системы перспективы, содержащие две или три
исчезающие точки, также являются излюбленной темой многих художников. К ним
также относится родственная область - анаморфное искусство.Dick Termes
"Клетка для человека"
(1978)
Слайд 10НЕВОЗМОЖНЫЕ ФИГУРЫ
Невозможные фигуры - эти фигура, изображенная в перспективе таким
способом, чтобы выглядеть на первый взгляд обычной фигурой. Однако при
более внимательном рассмотрении зритель понимает, что такая фигура не может существовать в трехмерном пространстве. Эшер изобразил невозможные фигуры на своих известных картинах "Бельведер"Невозможные фигуры - эти фигура, изображенная в перспективе таким способом, чтобы выглядеть на первый взгляд обычной фигурой. Однако при более внимательном рассмотрении зритель понимает, что такая фигура не может существовать в трехмерном пространстве. Эшер изобразил невозможные фигуры на своих известных картинах "Бельведер" (1958), "Восхождение и спуск"Невозможные фигуры - эти фигура, изображенная в перспективе таким способом, чтобы выглядеть на первый взгляд обычной фигурой. Однако при более внимательном рассмотрении зритель понимает, что такая фигура не может существовать в трехмерном пространстве. Эшер изобразил невозможные фигуры на своих известных картинах "Бельведер" (1958), "Восхождение и спуск" (1960) и "Водопад" (1961). Одним из примеров невозможной фигуры служит картина современного венгерского художника Иштвана ОросаСлайд 11ЛЕНТА МЕБИУСА
Лента Мебиуса - это трехмерный объект, имеющий только одну
сторону. Такая лента может быть легко получена из полоски бумаги,
перекрутив один концов полоски, а затем склеив оба конца друг с другом. Эшер изобразил ленту Мебиуса на работах "Всадники" (1946), "Лента Мебиуса II (Красные муравьи)" (1963) и "Узлы" (1965).Слайд 12ФРАКТАЛЫ
Фрактал - это объект, повторяющий сам себя в различных масштабах,
которые связаны математическим способом. Фракталы формируются итерационно, многократно повторяя вычисления
так, что получается объект высокой сложности с множеством мелких деталей. К сожалению, фракталы как таковые были недоступны Эшеру, потому что были формализованы и выделены в отдельную область математики лишь после его смерти. Эшер очень интересовался изображением бесконечного в пределах конечной области, в частности бесконечными тесселляциями. Он использовал сжимающиеся координатные сетки и гиперболическую геометрию для достижения этого эффекта, как показано в картинах "Предел круга" I-IV (1958-1960) и "Предел квадрата" (1964). Ниже приведены примеры современных художников Кэри Митчелл и Роберта Фатауэра.Слайд 13KERRY MITCHELL "БУДДА" - КОМПЬЮТЕРНАЯ КАРТИНА ОСНОВАННАЯ НА МНОЖЕСТВЕ МАНДЕЛЬБРОТА,
ИССЛЕДОВАННОГО БЕНУА МАНДЕЛЬБРОТОМ
Слайд 14ROBERT FATHAUER "КОМПОЗИЦИЯ КРУГОВ" (2001) - НЕ ЯВЛЯЕТСЯ ВЫЧИСЛЯЕМЫМ ФРАКТАЛОМ,
ОДНАКО МОЖЕТ БЫТЬ ПОЛУЧЕН ГРАФИЧЕСКИ, УПАКОВЫВАЯ МЕНЬШИЕ КРУГИ В БОЛЬШИХ.
Слайд 15СВЯЗЬ МАТЕМАТИКИ И ИЗОБРАЗИТЕЛЬНОГО ИСКУССТВА ПРИ КОНСТРУКТИВНОМ ПОСТРОЕНИИ НАТЮРМОРТА.
Натюрморт
(фр. nature morte — букв. «мертвая природа») — изображение неодушевлённых предметов в
изобразительном искусстве, в отличие от портретной, жанровой, исторической и пейзажной тематики.При построении натюрморта используются такие понятия как: параллельные прямые, геометрические фигуры, отношения, пропорции, оси симметрии. Приведём пример построения на простейшем натюрморте, состоящем из трёх предметов(ваза, кружка, груша)
Слайд 16
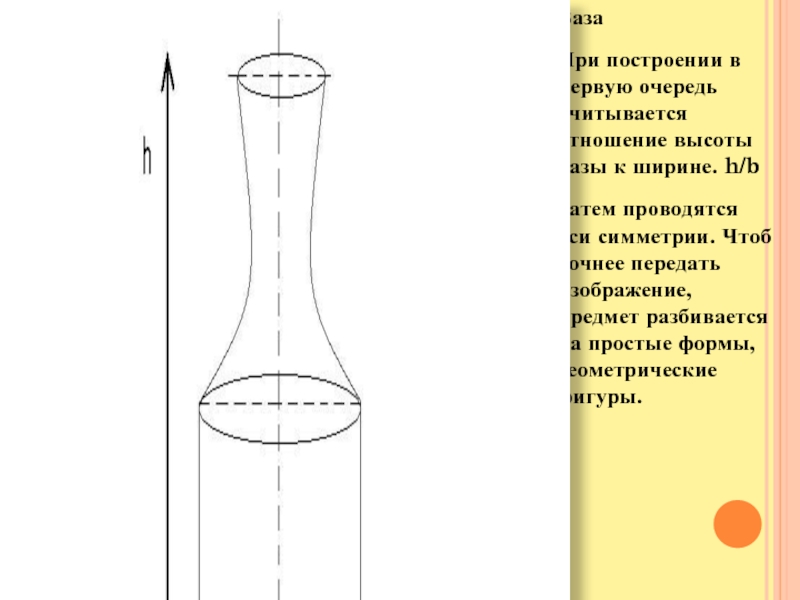
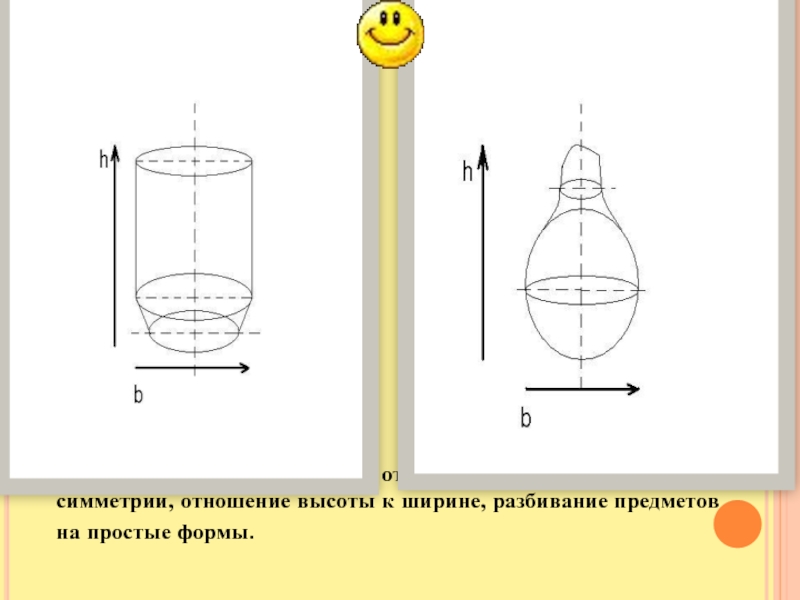
Ваза
При построении в первую очередь учитывается отношение высоты вазы к
ширине. h/b
Затем проводятся оси симметрии. Чтоб точнее передать изображение, предмет
разбивается на простые формы, геометрические фигуры. Слайд 18То же самое проделывается и в отношении кружки и груши.
Оси симметрии, отношение высоты к ширине, разбивание предметов на простые
формы.Слайд 20Соединяем три элемента . При этом мы должны учитывать
отношение размеров
предметов относительно друг друга, т. е. сколько раз высота груши
помещается в высоту вазы, ширина кружки в высоту груши и т. д. При построении овалов учитывается перспектива, чем ниже овал относительно уровня глаз, тем больше он раскрыт. Все оси овалов в каждом предмете строго параллельны друг другу. Кружка и ваза строго симметричны относительно осей симметрии.Слайд 21МНОГИЕ ХУДОЖНИКИ В СВОИХ РАБОТАХ ИСПОЛЬЗУЮТ МАТЕМАТИКУ. НАДЕЮСЬ, ЧТО В
СВОЕЙ РАБОТЕ Я ДОКАЗАЛА, ЧТО, КАЗАЛОСЬ БЫ, ТАКИЕ ОТДАЛЁННЫЕ ДИСЦИПЛИНЫ
КАК МАТЕМАТИКА И ИЗОБРАЗИТЕЛЬНОЕ ИСКУССТВО ПЕРЕСЕКАЮТСЯ ДРУГ С ДРУГОМ, А В ТВОРЧЕСТВЕ НЕКОТОРЫХ ХУДОЖНИКОВ ОНИ ОЧЕНЬ ТЕСНО СВЯЗАНЫ.
Теги