Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Медиана
Содержание
- 1. Медиана
- 2. Описательная статистикаМедиана (2 часа)Бахова А.Б. МОУ СОШ №6
- 3. Не только среднее арифметическое показывает, где на
- 4. Пример 1Возьмем какой-нибудь набор различных чисел, например
- 5. Пример 2Рассмотрим набор 1, 3, 6, 11.
- 6. Пример 3(а)Найти медиану набора 12, 2, 11,3,
- 7. Пример 3 (б)Найти медиану набора 12, 2,
- 8. Пример 3 (в)Найти медиану набора 1, 2,
- 9. Определение 1. Медианой набора различных чисел называют
- 10. Пример 4Производство пшеницы в России в 1995-2001
- 11. Пример 5В России в 2002 г. было
- 12. Пример 5 (продолжение)1. Найти среднее значение численности
- 13. Упражнения№1 Вычислите медиану и среднее арифметическое чисел,
- 14. №3 Отметьте числа и их медианы на
- 15. №6 Найдите медиану следующих наборов чисел:2, 4,
- 16. №8 Рассмотрите данные о числе жителей крупнейших
- 17. №10 Выпишите из таблицы 4 города, число
- 18. Скачать презентанцию
Слайды и текст этой презентации
Слайд 3Не только среднее арифметическое показывает, где на числовой прямой располагаются
числа какого-либо набора и где их центр.
Другим показателем является
медиана. Медианой набора чисел называют такое число, которое разделяет набор на две равные по численности части. (Вместо «медиана» можно было бы сказать «середина».)
Слайд 4Пример 1
Возьмем какой-нибудь набор различных чисел, например 1, 4, 7,
9, 11.
Подберем число m так, чтобы в наборе оказалось
поровну чисел, которые меньше и которые больше чем m.
На пробу возьмем m=5. В нашем наборе два числа меньше чем 5 (это 1 и 4), и три числа больше чем 5: это 7, 9 и 11. Значит, число 5 не годится.
Теперь возьмем m=7. Меньше числа 7 два числа, больше числа 7 тоже два числа. Следовательно, число 7 делит этот набор на две равные по численности части: (1 и 4) и (9 и 11), само оставаясь посредине набора. Число 7 – медиана набора чисел 1,4, 7,9,11.
В этом примере набор состоял из 5 чисел, записанных в порядке возрастания. Медианой в этом случае оказывается число, стоящее в точности посередине.
Слайд 5Пример 2
Рассмотрим набор 1, 3, 6, 11. Найти медиану набора.
Числа
тоже записаны по возрастанию, но их четыре, поэтому среди них
нет числа, стоящего точно посередине.Любое число из интервала (3,6) разделяет наш набор на две равные по численности части (1 и 3) и (6 и 11).
Медианой этого набора служит любое число, которое больше 3 и меньше 6. По определению в качестве медианы в таких случаях берут центр срединного интервала.
В нашем случае это центр интервала (3,6). Это полусумма его концов
Число 4,5 – медиана этого набора.
Слайд 6Пример 3(а)
Найти медиану набора 12, 2, 11,3, 7, 10, 3.
Расположим
числа по возрастанию: 2, 3, 3, 7, 10, 11, 12.
Будем
убирать числа одновременно с обоих концов набора. Получим последовательные наборы:2, 3, 3, 7, 10, 11, 12
3, 3, 7, 10, 11
3, 7, 10
7
Медианой будет число 7.
Слайд 7Пример 3 (б)
Найти медиану набора 12, 2, 11, 3, 7,
10, 3, 15.
Расположим числа по возрастанию: 2, 3, 3, 7,
10, 11, 12, 15.Будем убирать одновременно с обоих концов набора числа. Получим последовательные наборы:
2, 3, 3, 7, 10, 11, 12, 15
3, 3, 7, 10, 11, 12
3, 7, 10, 11
7, 10
Медианой может служить любое число, большее либо равное 7 и меньшее либо равное 10, но обычно в качестве медианы берут полусумму чисел 7 и 10.
8,5 – медиана набора.
Слайд 8Пример 3 (в)
Найти медиану набора 1, 2, 2, 2, 3,
3.
Расположим числа по возрастанию: 1, 2, 2, 2, 3, 3
Будем
убирать одновременно с обоих концов набора. Получим последовательные наборы:1, 2, 2, 2, 3, 3
2, 2, 2, 3
2, 2
2 – медиана набора.
Слайд 9
Определение 1. Медианой набора различных чисел называют такое число (скажем
m), которое обладает следующим свойством: количество чисел набора, меньших либо
равных m, равно количеству чисел набора, больших либо равных m.Определение 2. Медианой набора n чисел (среди которых могут быть совпадающие), называется
число, стоящее посередине (на месте с номером [n/2]+1) в упорядоченном по возрастанию ряду этих чисел, если n нечетно,
полусумма чисел, стоящих на средних местах (с номерами n/2 и n/2+1) в упорядоченном наборе этих чисел, если n четно.
Слайд 10Пример 4
Производство пшеницы в России в 1995-2001 гг. млн.тонн
Средний урожай
равен
Найдем медиану:
27,0; 30,1; 31,0; 34,5; 34,9; 44,3; 47,0
30,1; 31,0; 34,5; 34,9; 44,3; 31,0; 34,5; 34,9;
34,5 млн. тонн - медиана
Слайд 11Пример 5
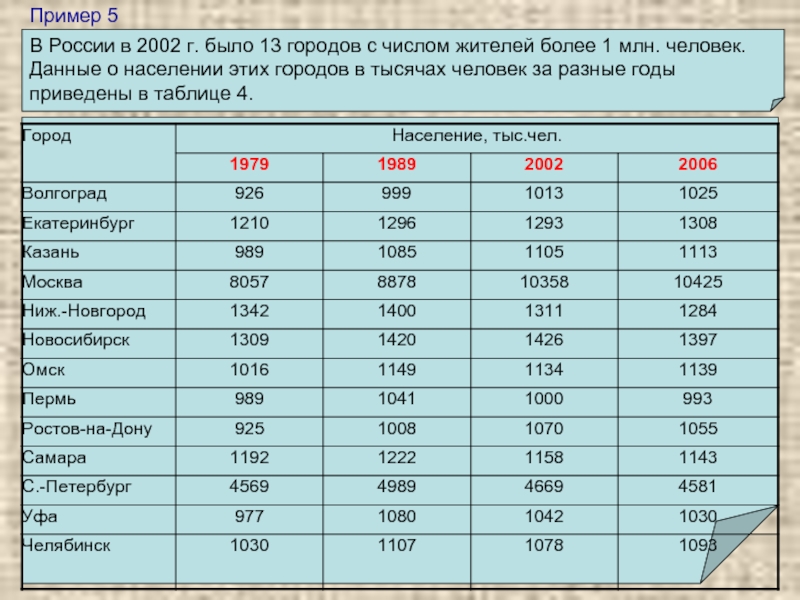
В России в 2002 г. было 13 городов с
числом жителей более 1 млн. человек. Данные о населении этих
городов в тысячах человек за разные годы приведены в таблице 4.
Слайд 12Пример 5 (продолжение)
1. Найти среднее значение численности жителей этих городов
в 2002 г.
Заметим, что нет в таблице города население которого
было бы близко к среднему значению. Значит среднее арифметическое не дает представление о населении «среднего», «типичного» города. Лучшее представление о населении «среднего», «типичного» города-миллионера дает медиана.
2. Упорядочим числа за 2002 год и найдем медиану:
Медиана равна 1134 тыс. человек. Это население г.Омска.
Слайд 13Упражнения
№1 Вычислите медиану и среднее арифметическое чисел, сравните медиану и
среднее значение:
1, 3, 5, 7, 9;
1, 3, 5, 7, 14;
1,
3, 5, 7, 9, 11;1, 3, 5, 7, 9, 16.
№2 Пользуясь таблицей 4, укажите:
Самый большой город России по числу жителей в 2002 г.;
Второй по населению город в России в 2002 г.;
Третий и четвертый по числу жителей города в России в 2002г.
Слайд 14№3 Отметьте числа и их медианы на числовой оси:
8, 11,
3;
7, 4, 8, 1, 5;
10, 3, 9, 8, 4, 5,
7.№4 Отметьте числа и их медианы на числовой оси:
9, 11, 3, 17;
7, 4, 8, 1, 5, 6;
11, 3, 9, 8, 13, 4, 5, 7.
№5 Найдите медиану следующих наборов чисел:
3, 4, 11, 17, 21;
17, 18, 19, 25, 28;
25, 25, 27, 28, 29, 40, 50.
Слайд 15№6 Найдите медиану следующих наборов чисел:
2, 4, 8, 9;
1, 3,
5, 7, 8, 9;
10, 11, 11, 12, 14, 17, 18,
22.№7 Пользуясь таблицей 4, ответьте на вопросы.
Насколько изменилось среднее число жителей крупнейших городов России в 2006 г. по сравнению с 2002 г.? Можно ли считать, что их население в среднем возросло за этот период?
Насколько изменилось среднее число жителей крупнейших городов России в 2006 г. по сравнению с 1989 г.? Можно ли считать, что их население в среднем возросло за этот период?
Найдите медиану числа жителей городов в 1989 г. Сравните ее с медианой, вычисленной для 2002 г. (1134 тыс. человек).
Слайд 16№8 Рассмотрите данные о числе жителей крупнейших городов России (таблица
4), исключив из них Москву и Санкт-Петербург, как города, имеющие
федеральный статус.Вычислите среднее значение числа жителей для этих городов в 2006 г.
Вычислите медиану числа жителей для этих городов в 2006 г.
Сильно ли отличаются медиана и среднее значение для этих городов?
№9 Рассмотрите данные о числе жителей крупнейших городов России в 1989 г. (таблица 4), исключив из них Москву и Санкт-Петербург.
Найдите среднее число жителей.
Найдите медиану числа жителей.
Сравните среднее значение и медиану числа жителей в 1989 г. с этими же характеристиками в 2006 г.
Слайд 17№10 Выпишите из таблицы 4 города, число жителей которых превышало
1 млн. человек в 1979 г. Найдите медиану числа жителей
этих городов:а) в 1979 г.; в) в 1989 г.; г) в 2002 г.; д) в 2006 г.
№11 В таблице 5 представлена урожайность зерновых культур в России.
Таблица 5. Урожайность зерновых культур а России в 1992-2001 гг.
По данным таблицы 5 вычислите медиану урожайности и среднюю урожайность зерновых культур в России за период:
а) 1992-2001 гг. б) 1992-1996 гг. в) 1997-2001 гг.
Сравните медиану и среднее. Насколько они отличаются друг от друга?