Слайд 1
В науке о числах… надо ожидать весьма
многого от наблюдений, ибо они постоянно приводят нас к новым свойствам,
над доказательством которых приходится
работать.
Л. Эйлер
тема проекта:
«Последовательность Фибоначчи и её загадки»
Над проектом работала: Цагараева Фариза,
ученица 8а класса МОУ СОШ34
г.Владикавказа, РСО Алания
Руководитель проекта: Ляликова Н.В.
учитель математики.
2010 г.
Слайд 2Цель исследования:
Установить закономерность ряда Фибоначчи и исследовать его свойства.
Задачи исследования:
Изучение
литературы с целью получения информации о последовательности Фибоначчи;
Продолжить исследование свойств
последовательности и установить их связь с явлениями в человеческом обществе, с литературой и искусством;
Уметь обрабатывать информацию;
Развивать умение анализировать и делать выводы;
Научиться коротко излагать свои мысли.
Методы исследования:
Теоретический и практический.
Слайд 3Гипотеза:
Если закономерность, которой подчиняются числа, составляющие последовательность Фибоначчи существует, то
она должна проявляться в законах природы, хронологии истории, в литературных
произведениях, в работах художников.
Слайд 4Вступление.
Цифры – это своеобразный язык, на котором общаются все. И
понимают его тоже все.
Если у вас есть хоть капля
эстетического чутья, то вы наверняка замечали негармоничность , искусственность человеческих творений, окружающих нас. Только истинные таланты радуют нас своими удивительными творениями. А в природе даже потёртая ветрами ветка или сорняк-замухрышка, всегда гармоничны и естественны.
Человеческие порождения часто плоды логических построений. А для гармонии нужны союз творчества и души.
Но в обоих случаях правит бал математика. Точнее, язык цифр.
Собираясь что-нибудь натворить, мы обзаводимся линейкой или сантиметром, или еще каким-либо хитрым измерительным прибором. Рассчитываем размеры, чтобы все сложилось и притерлось.
А у природы другая математика…
Слайд 5Леонардо Фибоначчи.
Итальянский купец Леонардо из Пизы ( 1180-1240), более известный
под прозвищем Фибоначчи был, безусловно, самым значительным математиком средневековья. Роль
его книг в развитии математики и распространении в Европе математических знаний трудно переоценить. Жизнь и научная карьера Леонардо теснейшим образам связаны с развитием европейской культуры и науки.
Слайд 6Научные трактаты Фибоначчи
Это обширнейшая «Книга абака», написанная в 1202 году,
но дошедшая до нас во втором своем варианте, который относится
к 1228 г.; «Практика геометрии»(1220г.); «Книга квадратов»( 1225г.).
По этим книгам, превосходящим по своему уровню арабские и средневековые европейские сочинения, учили математику чуть ли не до времен Декарта ( 17 в.).
Наибольший интерес представляет сочинение "Книга абака". Эта книга представляет собой объемный труд, содержащий почти все арифметические и алгебраические сведения того времени и сыгравший значительную роль в развитии математики в Западной Европе в течение нескольких следующих столетий. В частности, именно по этой книге европейцы познакомились с индусскими ("арабскими") цифрами.
Слайд 7Последовательность Фибоначчи
Эта последовательность является одной из самых интригующих страниц в
истории математики.
Например, сумма двух соседних чисел последовательности дает значение
следующего за ними (например, 1+1=2; 2+3=5 и т.д.), что подтверждает существование так называемых коэффициентов Фибоначчи, т.е. постоянных соотношений.
Одно из самых главных следствий этих свойств различных членов последовательности определяются следующим образом:
Слайд 8Последовательность Фибоначчи
1. Отношение каждого числа к последующему более и более
стремится к 0.618 по увеличении порядкового номера. Отношение же каждого
числа к предыдущему стремится к 1.618 (обратному к 0.618). Число 0.618 называют (ФИ), и мы поговорим о нем подробнее немного позже.
2. При делении каждого числа на следующее за ним через одно получаем число 0.382, наоборот - соответственно 2.618.
3. Подбирая таким образом соотношения, получаем основной набор фибоначчиевских коэффициентов: ... 4.235,2.618, 1.618,0.618,0,382,0.236. упомянем также 0.5 (1/2). Все они играют особую роль в природе, и в частности — в техническом анализе.
Важно отметить, что Фибоначчи как бы напомнил свою последовательность человечеству. Она была известна еще древним грекам и египтянам. И действительно, с тех пор в природе, архитектуре, изобразительном искусстве, математике, физике, астрономии, биологии и многих других областях были найдены закономерности, описываемые коэффициентами Фибоначчи.
Слайд 9Золотой коэффициент
Золотой коэффициент используется природой для построения ее частей, начиная
от больших и заканчивая малыми. Современная наука считает, что Вселенная
развивается по так называемой золотой спирали, которая строится именно с помощью золотого коэффициента. Эта спираль в буквальном смысле не имеет конца и начала. Меньшие витки никогда не сходятся в одну и ту же точку, а большие неограниченно развиваются в пространстве.
Самое важное заключается в том, что с помощью всех этих, в каком-то роде мистических, чисел, описываются разнородные процессы во Вселенной.
Слайд 10Мистический ряд Фибоначчи.
Мистический смысл последовательности
Фибоначчи заключен в том, что
она проявляется в
различных проекциях, так и не давая ответа
на
вопрос, как число φ = 1, 618 связано с тем или иным
явлением. Последовательность Фибоначчи – это не
просто игра с числами, а самое важное
математическое выражение природных явлений из
всех когда-либо открытых. Дотошные аналитики
выяснили, что события, которые повлияют на нашу
жизнь, появляются только тогда, когда совпадут
время и амплитуда, уготованная им рядом
Фибоначчи…
Мистический ряд Фибоначчи.
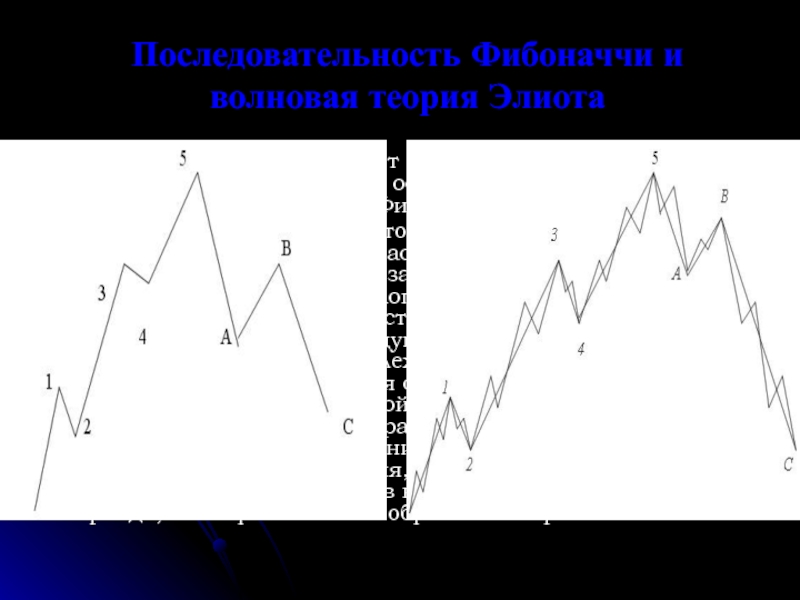
Слайд 11Последовательность Фибоначчи и волновая теория Элиота
Как признавал Ральф
Элиот в своей работе «Законы природы», математической основой его теории
стала последовательность чисел Фибоначчи. Главное открытие
Р. Элиота состояло в том, что поведение «толпы» – будь то рыночные торговцы или участники биржевой игры – подчиняется характерным законам. По его мнению, социально-массовое психологическое поведение последовательно проходит стадии экспансии, энтузиазма и эйфории, за которыми следуют успокоение, упадок и депрессия. Эта схема прослеживается в различных периодах времени, начиная с нескольких минут и заканчивая веками. Основой Теории служит так называемая волновая диаграмма. Волна – ясно различимое ценовое движение. Следуя правилам психологического поведения, все движения цен разбиваются на пять волн в направлении более сильного тренда, и на три волны – в обратном направлении.
Слайд 12 Один из простейших способов применения чисел Фибоначчи на практике
- определение отрезков времени, через которые произойдет то или иное
событие, например, изменение тренда.
ТРЕНД — направленность изменения экономических показателей, определяемая путем обработки отчетных, статистических данных и установления на этой основе тенденций экономического роста или спада.
Под трендом понимают также расчетную спрямляемую кривую изменения экономического показателя, построенную путем математической обработки статистических данных, на основе динамических рядов.
Аналитик отсчитывает определенное количество фибоначчиевских дней или недель (13, 21,34, 55 и т.д.) от предыдущего сходного события.
Числа Фибоначчи имеют широкое применение при определении длительности периода в Теории Циклов. За основу каждого доминантного цикла берется определенное количество дней, недель, месяцев, связанное с числами Фибоначчи. Например, длина Цикла (Волны) Кондратьева равна 54 годам. Отметим близость этой величины к фибоначчиевскому числу 55. Один из способов применения чисел Фибоначчи — построение дуг. Более подробно на этом способе применения чисел Фибоначчи я остановлюсь в своей следующей работе.

Слайд 13Числовая последовательность Фибоначчи в поэзии А. С. Пушкина.
В результате
проделанного мной исследования, я установила, что наиболее часто в творчестве
поэта встречаются стихи с таким количеством строк, которые тяготеют к данной числовой последовательности: 5, 8, 13, 21, 34. Наиболее выдающиеся шедевры, состоящие из 8 строчек, – это “Я вас любил”, “Пора, мой друг, пора! Покоя сердце просит”. 13-14 строчек в стихах “Сонет”, “Мадонна”, “Няне”. По 20 строчек – “Храни меня, мой талисман”, “Во глубине сибирских руд”, “К Чаадаеву”, “Памятник”.
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …
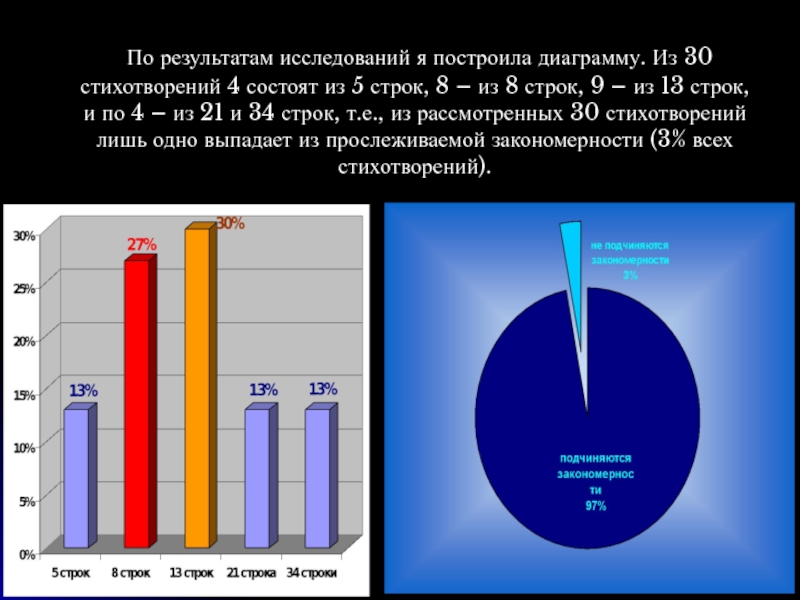
Слайд 14 По результатам исследований я построила диаграмму. Из 30 стихотворений 4
состоят из 5 строк, 8 – из 8 строк, 9
– из 13 строк, и по 4 – из 21 и 34 строк, т.е., из рассмотренных 30 стихотворений лишь одно выпадает из прослеживаемой закономерности (3% всех стихотворений).
Слайд 151, 1, 2, 3, 5, 8, 13, 21, 34, 55,
89, …
То, что количество строк в стихах Пушкина соответствует числам
Фибоначчи, – вовсе не случайность и не слепая игра вероятности. Это закономерность творческого восприятия поэта, интуитивное чувство гармонии. Хотя сам поэт признавал, что нельзя “алгеброй гармонию разъять”, но математические законы действуют в его поэзии независимо от автора. Другое высказывание Пушкина сближает две далёкие друг от друга науки: математику и литературу. Оно звучит так: ” Вдохновение нужно в поэзии, как в геометрии”.
Слайд 16Евгений Онегин
Знаменитый роман в стихах “Евгений Онегин” состоит из 8
глав, в каждой главе в среднем 50 стихов (а в
7-ой главе 55), а каждый стих состоит из 14 строчек. Основная схема построения “Евгения Онегина” основана на близости к трём числам Фибоначчи: 8, 13, 55. Интуиция Пушкина была необычайно сильной и плодотворной. Это основа его гениальности.
Проведенный Н. Васютинским анализ стихотворений А. С. Пушкина показал, что размеры стихов распределены весьма неравномерно; оказалось, что Пушкин явно предпочитает размеры в 5, 8, 13, 21 и 34 строк (числа Фибоначчи). Представляет несомненный интерес анализ романа «Евгений Онегин», сделанный Н. Васютинским. Этот роман состоит из 8 глав, в каждой из них в среднем около 50 стихов. Наиболее отточенной и эмоционально насыщенной является восьмая глава. В ней 51 стих. Вместе с письмом Евгения Онегина к Татьяне (60 строк) это точно соответствует числу Фибоначчи 55! Ритм онегинской строфы несет глубокую смысловую нагрузку. Четыре формообразующих элемента строфы - это, как правило, и четыре содержательных элемента: тема - развитие - кульминация - афористическая концовка. Онегинская строфа была настолько оригинальным и индивидуальным изобретением Пушкина, что после Пушкина почти никто из поэтов не рисковал прикасаться к его детищу.
Кульминацией главы является объяснение Евгения в любви к Татьяне -строка «Бледнеть и гаснуть ... вот блаженство!» Эта строка делит восьмую главу на две части - в первой 477 строк, а во второй - 295 строк. Их отношение равно 1, 617! Тончайшее соответствие величине золотой пропорции!

Слайд 17Пиковая дама
Обратимся вновь к произведениям А.С.Пушкина. Рассмотрим композицию "Пиковой дамы".
В этой повести кульминационным моментом является сцена в спальне графини,
куда проник Германн в надежде узнать тайну трех карт, сцена, которая оканчивается смертью графини в повести 853 строки. Кульминационный момент повести - это смерть графини. Ему отвечает 535 -я строка. Эта строка расположена в повести почти точно в месте золотого сечения, т.к. 853:535=1,6 . Повесть "Пиковая дама" состоит из шести глав. Посмотрим, не проявляется ли в композиции глав золотая пропорция? В первой главе золотому сечению отвечает 68 строчка (всего в главе 110 строк). Но ведь это же узловая точка повествования, в ней переломный момент всей главы: откроет ли Сен - Жермен свою тайну графине! Вторая глава повести содержит 219 строк. Золотое сечение здесь приходится на 135 строку. Но ведь это кульминационный момент главы, Лиза увидела в окне стоящего на улице Германна! Отсюда начался для нее новый отсчет времени, начались события, определившие всю ее дальнейшую судьбу. А.С.Пушкин совершенно точно определил это место во второй главе: ведь 219:135 = 1,62. Третья глава повести описывает усилия Германна попасть в дом старой графини, выведать у нее тайну трех карт. Это место начинает новый отсчет времени для Германна. Эта ситуация приходится на 131 строку третьей главы, а всего в ней 212 строк. Разделив 212 на 131, мы получим точно золотую пропорцию 1,618! В четвертой главе размером 113 строк золотая пропорция приходится на 70 строку. Это также переломный, трагический момент в жизни Лизы. В пятой главе описано посещение Германна похорон графини. 46 строка пятой главы разделила повествование на две части: первая - похороны графини и вторая - сон Германна. Эта 46 строка также отвечает золотой пропорции, ведь всего в этой главе 75 строк (75:46=1,63). В последней главе повести золотая пропорция приходится на 77 строчку, которая завершает описание первого дня игры Германна в карты и первого его выигрыша. Как видим, и в композиции последней главы повести присутствует золотая пропорция. Золотая пропорция присутствует и в композиции других произведений Пушкина. В рассказе "Станционный смотритель" 377 строк. Кульминационный момент рассказа - это известие о том, что дочь смотрителя уехала с гусаром. Этот момент отражен во фразе, которая является 214 строкой. Здесь почти точное соответствие золотой пропорции. В маленьком рассказе "Гробовщик" всего 229 строк. Со 139 строки начинается описание страшного сна гробовщика. И здесь переломный момент рассказа приходится почти точно на золотую пропорцию (229:1,618=141 строка). Совпадение кульминационных моментов в произведениях А.С.Пушкина с золотой пропорцией удивительно близкое, в пределах 1-3 строк.

Слайд 18Золотое сечение в картине И.И. Шишкина
«Сосновая роща»
На этой знаменитой
картине И. И. Шишкина с очевидностью просматриваются мотивы золотого сечения.
Ярко освещенная солнцем сосна (стоящая на первом плане) делит длину картины по золотому сечению. Справа от сосны - освещенный солнцем пригорок. Он делит по золотому сечению правую часть картины по горизонтали. Слева от главной сосны находится множество сосен - при желании можно с успехом продолжить деление картины по золотому сечению и дальше. Наличие в картине ярких вертикалей и горизонталей, делящих ее в отношении золотого сечения, придает ей характер уравновешенности и спокойствия, в соответствии с замыслом художника. Когда же замысел художника иной, если, скажем, он создает картину с бурно развивающимся действием, подобная геометрическая схема композиции (с преобладанием вертикалей и горизонталей) становится неприемлемой.
Слайд 19 Портрет Моны Лизы (Джоконда) Леонардо да Винчи привлекает тем, что
композиция рисунка построена на "золотых треугольниках", точнее на треугольниках, являющихся
кусками правильного звездчатого пятиугольника.
«Джоконда» и «золотые
Прямоугольники»
Слайд 20Заключение
Я думаю, что данная работа заинтересует не только учеников, интересующихся
математикой, но и будет интересна учащимся, которые любят литературу, другие
области знаний, а так же учителям.
Слайд 21Выводы.
Полученные результаты исследований дают возможность утверждать, что в природе и
в ходе развития человеческой цивилизации с достаточным постоянством повторяются числа
Фибоначчи.
Последовательность Фибоначчи остается математической кабалой и по сей день, и каждое новое открытие бросает новый отблеск на магию этих цифр.
Может быть эти загадочные цифры ведут нас к разгадке великой тайны – Тайны Жизни?...
Слайд 22Информационные ресурсы:
Воробьёв Н.Н. Числа Фибоначчи. -М.: Наука,1969.
Виленкин Н.Я. И др.
Комбинаторика.- М. :ФИМА, МЦНМО, 2006.
Васютинский Н.А. Золотая пропорция.- М., Молодая
гвардия,1990.
Гринбаум О.Н. Онегинская строфа.
http://samara.teletrade.ru/glossary/tech/index
http://www.membrana.ru
http:// www.google.com
http:// www.exponenta.ru
http:// www.1september.ru