Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Метапредметные результаты проектной деятельности по математике
Содержание
- 1. Метапредметные результаты проектной деятельности по математике
- 2. Метод проектов по своему стратегическому замыслу нацелен
- 3. Темы проектовВеликая пирамида- математическое чудоБактерии, вирусы и
- 4. Метапредметные результатыУчащиеся учатся анализу ситуации и постановке
- 5. Приобретают первичные навыки свертывания информации на этапе
- 6. Слайды из проекта «Великая Пирамида-математическое чудо»
- 7. Молекула ДНК похожа
- 8. Существует другая связь,
- 9. Учащийся 9 класса провел серьезные исследования параметров
- 10. Проект «Бактерии, вирусы и математика»Это исследовательская работа,
- 11. • Большинство изученных вирусов имеют диаметр в
- 12. Слайд 12
- 13. • Спиральный - эти капсиды состоят из
- 14. Продолговатыми называют икосаэдрические капсиды, вытянутые вдоль оси
- 15. СИММЕТРИЯ ВИРУСОВ • Икосаэдрический тип- капсомеры, или
- 16. • Комбинированный тип (смешанный) - симметрия
- 17. Проект «Насекомые и математика»Это долгосрочный проект, который
- 18. ШМЕЛИНАЯ математика, или как насекомые решают «задачу
- 19. Золотое сечение в живой природеВ биологических исследованиях
- 20. У многих бабочек соотношение размеров грудной и
- 21. «Математический журнал»Рубрика:Старинные математические задачи
- 22. Проект «насекомые и математика»
- 23. Рубрика «Красота своими руками»
- 24. Вывод:Включение проектной деятельности в образовательный процесс способствует
- 25. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Метапредметные результаты проектной деятельности по математике
Выполнила: Монахова Елена Васильевна
МБОУ СОШ
№18 г.о.Коломна, Московской области
Слайд 2Метод проектов по своему стратегическому замыслу нацелен на формирование способностей,
позволяющих эффективно действовать в реальной жизненной ситуации.
Обладая такого рода способностями,
ребенок может адаптироваться к изменяющимся условиям, может успешно ориентироваться в разнообразных ситуациях.Слайд 3Темы проектов
Великая пирамида- математическое чудо
Бактерии, вирусы и математика
Насекомые и математика
Решение
задач на смеси и сплавы
Теорема Пифагора за рамками школьной программы
Слайд 4Метапредметные результаты
Учащиеся учатся анализу ситуации и постановке цели, планированию деятельности
в начале работы над проектом
При планировании проекта учатся слушать собеседника,
вести диалог, учатся умению договариваться о распределении функцийФормируется ответственность за общее благополучие и уважительное отношение к другому мнению, приобретаются навыки разрешения конфликтов
Учатся работать с различными видами справочной литературы, разными источниками информации
Слайд 5Приобретают первичные навыки свертывания информации на этапе ее поиска, используют
средства ИКТ для решения коммуникативных и познавательных задач
При защите проекта
учатся строить свои речевые высказывания, соблюдать нормы этики и этикетаНа этапе защиты проекта приобретают навыки экспертизы своей и чужой деятельности, учатся критериям оценки сильных и слабых сторон работы над проектом
На всех этапах они овладевают предметными и межпредметными понятиями ( тесная связь с историей, биологией, физикой, информатикой, изо и др. предметами
Слайд 7 Молекула ДНК похожа на продольно закрученную
веревочную лестницу, где боковые стороны составляются остатками сахара и фосфорной
кислоты, а «ступеньки» образованы азотистыми основаниями.«первое» чудо: средний угол причленения азотистых оснований 51045’, а в пирамиде Хеопса угол наклона граней 51051’
«второе» чудо: отношение диаметра молекулы ДНК (20 ангстрем) к длине шага спирали (34 ангстрема) равно 0,588. Если же мы разделим апофему грани пирамиды Хеопса(187м) на диагональ основания (329м), получим 0,568 – почти то же самое
«третье» чудо: угол возрастания спирали ДНК равен 260, и угол наклона главной галереи в пирамиде Хеопса – тоже 260
Слайд 8 Существует другая связь, значительно более глубокая,
основанная на ограничениях и разрешениях, существующих в природе.
Почему близки или кратны углы в молекуле ДНК и в пирамиде Хеопса, в клине журавлей, сотах пчел и многом другом? Да по тому, что углы эти не случайны. Они энергетически выгодны. Они не дают раньше времени осыпаться куче песка или разваливаться той же пирамиде Хеопса. И позволяют пирамидам стоять, бросая вызов времени… Слайд 9Учащийся 9 класса провел серьезные исследования параметров Великой пирамиды Хеопса.
Выводы данного проекта дают формирование целостной, научной картины мира, связи
цивилизаций, завораживают своей схожестью с объектами реального мира и, в частности, с современными данными биологии.Слайд 10Проект «Бактерии, вирусы и математика»
Это исследовательская работа, где ученики 9
класса просмотрели и отобрали из огромного количества материала по биологии
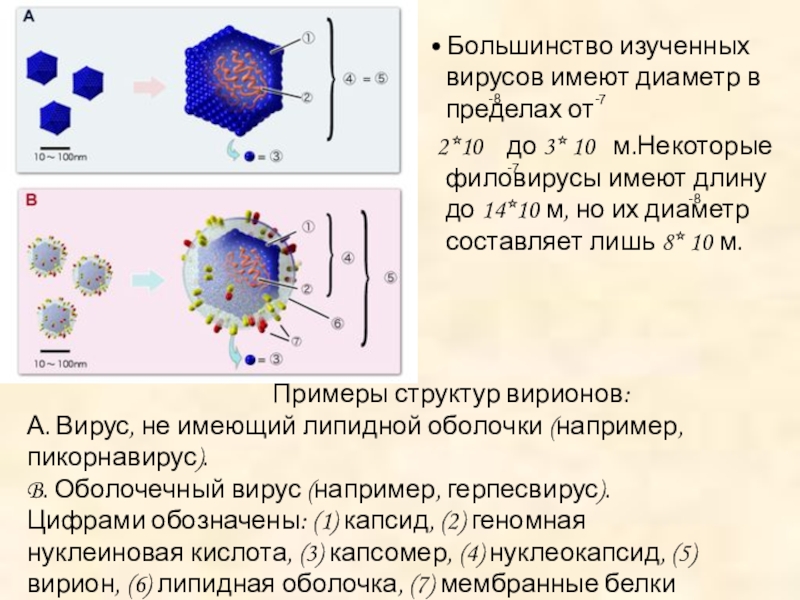
по данной теме информацию, тесно связанную с математикой, начиная от параметров бактерий и вирусов, заканчивая их геомерическими формамиСлайд 11• Большинство изученных вирусов имеют диаметр в пределах от
2*10 до 3* 10 м.Некоторые филовирусы имеют длину до 14*10
м, но их диаметр составляет лишь 8* 10 м. Примеры структур вирионов:
А. Вирус, не имеющий липидной оболочки (например,пикорнавирус).
B. Оболочечный вирус (например, герпесвирус).
Цифрами обозначены: (1) капсид, (2) геномная нуклеиновая кислота, (3) капсомер, (4) нуклеокапсид, (5) вирион, (6) липидная оболочка, (7) мембранные белки оболочки
-8
-7
-7
-8
Слайд 12 Классифицируют четыре
морфологических типа капсидов вирусов:
•спиральный;
•икосаэдрический;
•продолговатый ;
• комплексный.
Слайд 13• Спиральный - эти капсиды состоят из одного типа капсомеров,
уложенных по спирали вокруг центральной оси
(Вирус табачной
мозаики)Данная форма может быть представлена в
виде математического описания
n
функциональной зависимости F(x)=∑ n(y+k), где n- число копий белков, y и k –виды
белков. 1
• Большинство вирусов животных имеют икосаэдрическую или
почти шарообразную форму с икосаэдрической симметрией.
Минимальное необходимое число одинаковых капсомеров — 12, каждый капсомер состоит из пяти идентичных
n
субъединиц(т.е математически может быть представлено как F=∑5n,
min=12,n-максимальное число капсомеров) 12
Слайд 14Продолговатыми называют икосаэдрические капсиды, вытянутые вдоль оси симметрии пятого порядка.
Такая форма характерна для головок бактериофагов.
Может быть описана
в виде различной
функциональнойзависимости(к примеру, прямой : F(x)=ny )
Форма комплексных капсидов ни чисто спиральная, ни чисто икосаэдрическая. Они могут нести дополнительные наружные структуры, такие как белковые хвосты или сложные наружные стенки.
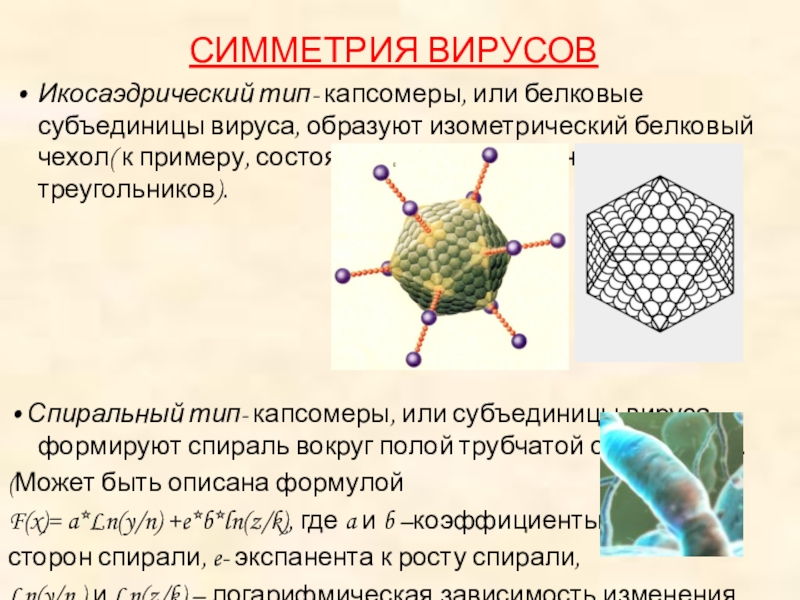
Слайд 15СИММЕТРИЯ ВИРУСОВ
• Икосаэдрический тип- капсомеры, или белковые субъединицы
вируса, образуют изометрический белковый чехол( к примеру, состоящий из 20
правильных треугольников).• Спиральный тип- капсомеры, или субъединицы вируса, формируют спираль вокруг полой трубчатой сердцевины.
(Может быть описана формулой
F(x)= a*Ln(y/n) +e*b*ln(z/k), где a и b –коэффициенты
сторон спирали, e- экспанента к росту спирали,
Ln(y/n ) и Ln(z/k) – логарифмическая зависимость изменения спирали.)
Слайд 16• Комбинированный тип (смешанный) - симметрия представлена разными вариантами.
Частица бактериофага может имеет "головку" правильной геометрической формы и "хвост"
со спиральной симметрией.• встречаются вирусы с еще более сложным строением. Вирионы поксвирусов (вирусы группы оспы) не имеют правильного, типичного капсида: между сердцевиной и наружной оболочкой у них располагаются трубчатые и мембранные структуры.
z
(Можно представить в виде комбинированной прогрессии K= ∑(a/n+ b/n
1
+…+ ∑m/n)
Слайд 17Проект «Насекомые и математика»
Это долгосрочный проект, который учащиеся 4 класса
начали 2 года назад и ежегодно дополняют новым материалом и
выходят в этом году на защиту с презентацией с помощью ИКТСлайд 18ШМЕЛИНАЯ математика, или как насекомые решают «задачу коммивояжёра»
Во время поиска
пищи шмелям приходится выбирать оптимальный маршрут
между цветками - иными
словами, им необходимо решить математическую задачу, которая порой требует помощи компьютера.
Слайд 19Золотое сечение в живой природе
В биологических исследованиях 70-90 гг. показано,
что, начиная с вирусов и растений и кончая организмом человека,
всюду выявляется золотая пропорция, характеризующая соразмерность и гармоничность их строения. Золотое сечение признано универсальным законом живых систем. Можно отметить два вида проявлений золотого сечения в живой природе: иррациональные отношения по Пифагору - 1.62 и целочисленные, дискретные - по Фибоначчи. Для всего животного мира характерны симметрия форм и наличие парных органов, членение на три части тела (голова, грудь, брюшко), членение конечностей на 3 и 5 частей, а брюшка - на 3. Это является характерной чертой морфологии насекомых