Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Показательные уравнения. Презентация к уроку
Содержание
- 1. Показательные уравнения. Презентация к уроку
- 2. Цели урокаВыявить общий вид показательного уравнения Выяснить способы его решенияНаучиться решать простейшие показательные уравнения.
- 3. В ходе радиоактивного распада масса изотопа изменяется
- 4. Девиз занятияХОЧУМОГУУМЕЮДЕЛАЮ
- 5. 1. Является ли показательной функция: y =
- 6. Проверка1-2 ответа – «2», 3 ответа –
- 7. Считаем устно. Представьте числа в виде
- 8. Вычислите1000025108640,0011298164
- 9. Притча“Однажды молодой человек пришел к мудрецу. Каждый
- 10. Простейшее показательное уравнение имеет вид:?x =?где ?
- 11. Примеры показательных уравнений.1. 5x-2 = 25 2.
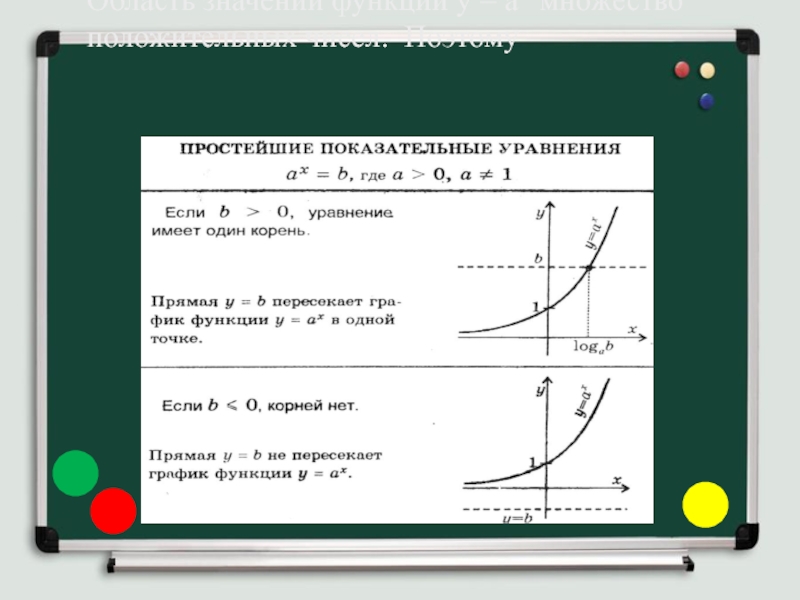
- 12. Область значений функции у = ах множество положительных чисел. Поэтому
- 13. Методы решения показательных уравнений Метод приведения степеней
- 14. Метод приведения степеней к одному основанию
- 15. 3x+2 + 3x = 903x · 32
- 16. 100x – 11 ⋅ 10x + 10
- 17. Метод почленного деления
- 18. Графический метод4х = 5-хВ одной координатной плоскости
- 19. М. В. Ломоносов говорил “Теория без практики
- 20. Физминутка
- 21. Работа в группах
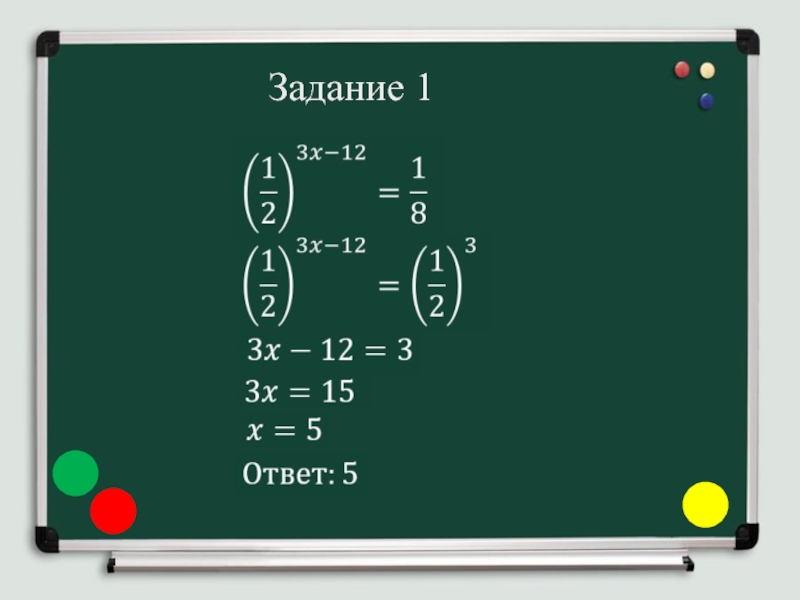
- 22. Задание 1
- 23. 3x+1 + 3x = 1083x ⋅ 3
- 24. 4x + 2 ⋅ 2x – 80
- 25. Тест « Решите уравнения»1 вариант2 вариант
- 26. Слайд 26
- 27. Итоги урокаКакие уравнения называются показательнымиСколько решений имеет
- 28. Мне все понятно, у меня все получается!Мне
- 29. Домашнее задание. Составить три показательных уравнения и решить их.
- 30. Спасибо за внимание !!!
- 31. Скачать презентанцию
Слайды и текст этой презентации
Слайд 3В ходе радиоактивного распада масса изотопа изменяется по формуле
, где m0 начальная масса изотопа, t время,
прошедшее с момента распада, Т период полураспада. Через сколько времени останется 5 грамм изотопа, если первоначально его было 40 грамм, а период полураспада 10.Задача
Слайд 51. Является ли показательной функция:
y = 5х + 2?
2.
Верно ли, что областью определения показательной функции является R?
3. Является
ли убывающей функция y = 2х ?4. Верно ли, что показательная функция y = ?х принимается наибольшее значение в некоторой точке x0?
5. Представить в виде степени:
3-2 · 81
1. Является ли показательной функция:
y = x5 + 2?
2. Верно ли, что график показательной функции проходит через точку с координатами (0;1)?
3. Является ли возрастающей функция y = (0,3)х ?
4. Верно ли, что показательная функция y = ?х принимается в некоторой точке значение равное нулю?
5. Представить в виде степени:
2-2 · 32
Математический диктант
Вариант 1
Вариант 2
Слайд 7 Считаем устно. Представьте числа в виде степени : 1/2;
8; 16; 27; 1/32; 64; 81; 100; 121; 125; 1000;
0,001.Слайд 9Притча
“Однажды молодой человек пришел к мудрецу. Каждый день по пять
раз я произношу фразу: “Я принимаю радость в мою жизнь”
Но радости в моей жизни нет. Мудрец положил перед собой ложку, свечу и кружку и попросил “Назови, что ты выбираешь из них”. “Ложку”, – ответил юноша. Произнеси это 5 раз.”. “Я выбираю ложку”, послушно произнес юноша 5 раз. “Вот видишь, – сказал мудрец, повторяй хоть миллион раз в день, она не станет твоей. ”Что же надо? - спросил ученик. «Надо протянуть руку и взять ложку» - был ответ мудреца.Слайд 10Простейшее показательное уравнение имеет вид:
?x =?
где ? > 0 и
? ≠ 1
Показательное уравнение - это уравнение, в котором неизвестное
содержится в показателе степениСлайд 13Методы решения показательных уравнений
Метод приведения степеней к одному основанию
Вынесение
общего множителя за скобки
Метод введения новой переменной
Метод почленного деления
Графический метод
Слайд 153x+2 + 3x = 90
3x · 32 + 3x =
90
3x(32 + 1) = 90
3x ⋅ 10 = 90
3x =
90 : 103x = 9
3x = 32
x = 2
Ответ: 2
Метод вынесения общего множителя за скобки
Слайд 16100x – 11 ⋅ 10x + 10 = 0
(10x)2 –
11 ⋅ 10x + 10 = 0
Пусть 10x = y
y2
– 11y + 10 = 0Д = 121 – 40 = 81
y1= 10; y2 = 1
1) 10x = 10; 2) 10x =1
X = 1 10x = 100
X = 0
Ответ: 0; 1
Метод введения новой переменной
Слайд 18Графический метод
4х = 5-х
В одной координатной плоскости строят графики функций
у = 4х и у = 5-х
Решением уравнения является абсцисса
точки пересечения графиков функций у = 4х и у = 5-х
Проверка: х = 1, 41 = 5-1, 4 = 4 (верно)
Ответ: х = 1.
Слайд 19М. В. Ломоносов говорил “Теория без практики мертва и бесплодна,
практика без теории невозможна и пагубна. Для теории нужны знания,
для практики сверх того, и умения” (портрет ученого вывешивается на доску). И вот теперь вы должны проявить свои умения при решении различных показательных уравнений.Слайд 233x+1 + 3x = 108
3x ⋅ 3 + 3x =
108
3x (3 + 1) =108
3x ⋅ 4 = 108
3x = 108 : 4
3x = 27
3x = 33
X = 3
Ответ: 3
Задание 2
Слайд 244x + 2 ⋅ 2x – 80 = 0
(2x)2 +
2 ⋅ 2x – 80 = 0
Пусть 2x = y
y2
+ 2y – 80 = 0Д = 4 – 4 ⋅ 1 (-80) = 324
y1 = 8; y2 = -10
1) 2x = 8; 2) 2x = -10
2x = 23 корней нет
X = 3
Ответ: 3
Задание 3
Слайд 26 Вариант 1
Вариант 2
№
п/п ответы № п/п ответы 1. -1 1. 3
2. 4 2. 10
3. 8 3. 4
4. 4 4. 0
5. -2 5. -0,2
Проверь себя